Construction de Q
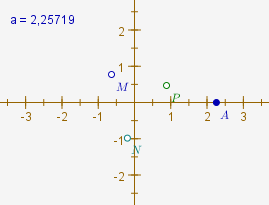
Puisque a est un réel variable, on va le rendre égal à x(A) où A est un point lié à l’axe des abscisses. Les coordonnées de M seront alors
rcos(a)
rsin(a)(angles en radians).
Pour construire N, on utilise la macro « produit de nombres complexes » en sélectionnant deux fois le point M, et pour créer P, on utilise la même macro en sélectionnant M et N.
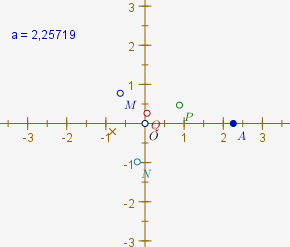
Comme la macro « somme de nombres complexes » n’attend que deux termes, on va l’appliquer deux fois, une fois en sélectionnant M et N (point marron en forme de « + ») et une fois avec le point nouvellement créé et P : On obtient alors Q :
Conjectures
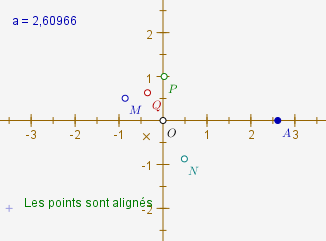
Pour O, N et Q, on utilise l’outil « test d’alignement » (dans « test »), en sélectionnant successivement O, N et Q :
On constate que l’affichage ne change pas lorsqu’on bouge A : Les points persistent à être alignés.
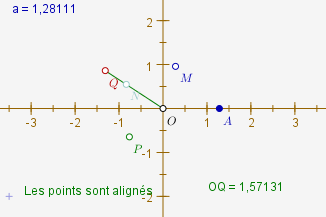
Pour La distance, on crée un segment s1 entre O et Q, et l’expression (en bas à droite) égale à « s1 » :
Lieu
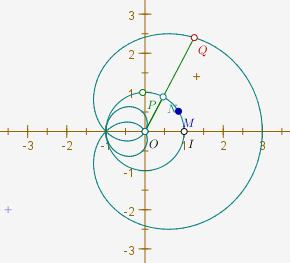
Bien que ce ne soit pas demandé par l’énoncé du TP, on eût pu considérer le point M comme un point sur le cercle unité et définir après coup a comme l’angle en radians entre I(1 ;0), O(0 ;0) et M. Dans ce cas [1], le lieu de Q (hors sujet pour ce TP) est plus précis :


Commentaires