CP1. Apprentissage de la soustraction au CP - Méthode Tchou

En particulier, utilisation d’un cache dont le fonctionnement précède les méthodes « en avançant » et « en reculant ».

Dans la démarche qui nous intéresse ici, l’apprentissage du calcul de la soustraction commence dès le CP. D’une manière symbolique et forte en terme de représentation, elle se pratique avec deux gestes physiques différents qui vont accompagner les deux gestes mentaux évoqués dans la présentation de Rémi Brissiaud.

Les premiers apprentissages commencent avec les petits nombres, inférieurs à 10, sur des cartes de constellations (faisant apparaître l’appui à 5) individuelles et collectives. On utilise un cache pour masquer les nombres de points à soustraire.

Le cache s’utilise « par le haut » pour soustraire des petits nombres, en pratique inférieurs à 5, et « par le bas » pour des grands nombres, supérieurs ou égaux à 5 pour cacher une constellation de 5.

Ce premier extrait vidéo montre les réussites et les difficultés des élèves sur cette mise en œuvre qui se pratique ici en avril, alors que l’addition est déjà bien structurée.

Chacun comprend bien la transposition utilisée dans cette méthode : la « droite numérique » ou la frise numérique, est liée aux cartes de constellation qui sont elles aussi orientées. Cacher par le haut correspond au geste de reculer sur la frise numérique alors que cacher par le bas correspond à l’avancement sur la frise numérique. On cache donc par le haut pour les petits nombres (inférieurs à la moitié du maximum) et par le bas pour les grands nombres (supérieurs à la moitié du maximum).

Comme on va le voir plus loin, les rudiments du calcul réfléchi peuvent se faire aussi ici — en pratique dès qu’il y a une règle sur les nombres. Mais il vont se faire sur les manipulations du cache : entrer dans le calcul réfléchi c’est s’émanciper des règles générales pour adapter le geste (physique d’abord puis mental ensuite) à la situation, avec une intelligence des nombres en jeux.

CP2. Soustraction - Entraînement aux procédures

Nous avons réuni ici quelques exemples d’utilisation collective du cache. Il s’agit de fixer, institutionnellement, les règles de l’utilisation du cache.

On notera également l’usage systématique du subitizing (reconnaissance visuelle globale) sur les petits nombres, ce qui permet aux élèves à la fois d’oublier le surcomptage (même si on peut voir que certains élèves l’utilisent encore sporadiquement) et de favoriser la fréquentation avec la décomposition additive (avec appuis à 5 éventuellement) pour une mémorisation des résultats.

On observera que la maîtresse rappelle la règle du cache, notamment à 1 min 52 s, elle dit « on cache par le bas les grands nombres, ça permet de cacher les 5 ».

CP3. Procédures d’organisation réfléchie de l’usage du cache

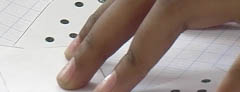
Nous sommes plus loin dans l’année avec les cartes de constellation jusqu’à 20. Il s’agit de calculer 14 - 5. L’élève étant hésitante pour reconnaître la constellation du 9 avec la procédure usuelle, l’enseignante propose alors une démarche que l’on appellera « d’organisation réfléchie » qui préfigure le calcul réfléchi ultérieur quand il utilisera la décomposition additive de manière pertinente : l’idée de cacher une constellation du 5 permet de donner une lecture plus simple du résultat.

Dans un premier temps l’élève construit le 14 comme 10 et 4 (comptine régulière de Tchou). En cachant 5 par le haut comme la règle de soustraction le stipule, l’élève ne reconnaît pas spontanément 9 dans sa configuration habituelle (5 et 4). La maîtresse, en proposant de cacher le 5 par le bas (ce qui n’est pas la procédure standard) montre à l’élève que le résultat est dans une configuration reconnue.

Ce que fait l’enseignante ici, c’est ouvrir l’arithmétique au choix, et à la pertinence. Elle engage ainsi l’élève vers ce qui sera le calcul réfléchi. C’est parce qu’il peut avoir le choix entre plusieurs procédures que l’élève acquiert une expertise des nombres.

On pourrait reprocher à la méthode d’être éloignée de ses ambitions premières (définition du calcul chez Brissiaud). Pourtant, tout en restant dans le domaine perceptif, la méthode met en évidence l’équivalence des procédures liées à la soustraction, mais aussi celles liées aux équivalences des décompositions additives.

Si la méthode semble rester longtemps dans le perceptif, c’est qu’elle construit aussi des habitudes de subitizing qui évitent le surcomptage : la vitesse de réponse de l’élève atteste bien qu’il y a reconnaissance du 9 comme 5 et 4.

Dans le second exemple (vers 1 min), un élève doit effectuer la soustraction 13 - 7. Bien qu’il s’agisse d’un élève qui n’utilise que rarement le comptage, le fait que 7 soit proche de la moitié de 13, il hésite sur la façon de cacher 7 et fait plusieurs tentatives (qu’on ne voit pas ici) pour finalement — c’est l’extrait retenu — cacher par le haut en comptant le nombre de points à enlever.

Lors de la correction, une autre élève cache par le bas et utilise les « petits doubles » pour reconnaître le résultat. On voit là encore deux procédures dont l’une est plus efficace que l’autre.

CP4. La soustraction en fin de CP

Dans un premier temps la maîtresse réactive la soustraction sur un exemple simple : 12 - 3. Nous avons choisi cet extrait pour illustrer que, contrairement à l’extrait précédent, des élèves voient directement 9 dans la configuration non standard. On peut penser que ces élèves sont plus dans le numérique, en tout cas font abstraction de l’outil perceptif.

L’extrait se poursuit sur une activité de calcul par visualisation mentale par reconstitution de la vison d’autrui comme expliqué à cette page pour l’addition. Il s’agit de faire 15 - 4. Pour cela les élèves passent par trois étapes.

Dans un premier temps, ils doivent visualiser 15 comme 10 et 5. Par son questionnement, la maîtresse sollicite cette visualisation. Dans un deuxième temps, en voyant le cache en haut, les élèves doivent se représenter le retrait de 4 (sur 5 car on travaille toujours avec des appuis à 5 ou 10).
Enfin, ils doivent visualiser 11 comme 10 et 1.

Remarque quant au support utilisé : pour une meilleure visualisation, tout d’abord un fond blanc et des grosses gommettes seraient préférables, et surtout, il serait plus efficace de préparer des supports mettant mieux en évidence les configurations de 5 : ici, on voit plus des configurations de 4 séparées par un 1 isolé.

S1a. Présentation et utilisation du matériel collectif

Après quelques exercices de calcul réfléchi sur la soustraction sur les petits nombres, comme vu dans les extraits précédents, dans cette séance, les élèves vont apprendre le calcul réfléchi de la soustraction de type a - b avec a ≤ 100.
On aborde ici le cas où l’on retire beaucoup pour enseigner la soustraction en avançant.

L’enseignant présente le matériel utilisé, à savoir une représentation d’une file de boîtes de Picbille que les élèves connaissent bien. Il s’agit de repérer les groupements de 10 pour pouvoir placer rapidement des nombres sur la file numérique.
On remarque les deux files de boîtes qui permettront de mettre en évidence deux façon de barrer les cases, et donc, en fait, l’équivalence des deux procédures qui vont être pratiquées par les élèves.

Remarque : en fait, à l’usage, il apparaît que les élèves éprouvent des difficultés à visualiser les groupements de 10 car on voit plus les marques du 5 que les espacements entre les groupes de 10 qui sont seulement sur des feuilles différentes.
Il conviendra d’être vigilant sur la réalisation de ce matériel.

Cette activité préliminaire est aussi une illustration de cette compétence attendue en fin de cycle 2 : « Comprendre et déterminer la valeur des chiffres en fonction de leur position dans l’écriture décimale d’un nombre ». Par exemple, 53 est pensé comme 5 dix et 3.

S1b. Première méthode spontanée (en avançant)

Il s’agit d’utiliser ce matériel pour effectuer « 46 - 39 ». Dans un premier temps on repère le 46 sur la file de boîtes et on transforme l’ordinalité en une cardinalité par une accolade (que l’enseignant écrit naturellement de gauche à droite).

Pour effectuer la soustraction un premier élève utilise spontanément la méthode en avançant, en proposant lui-même de rayer les 39 premières cases. Deux analyses de cette démarche sont possibles :

1) De par la pratique régulière du calcul réfléchi et de la visualisation mentale avec le cache, certains élèves se sont déjà affranchis du sens restrictif de la soustraction qui consiste à reculer sur la frise numérique. En effet, dans la visualisation mentale de la soustraction, le cache est utilisé parfois en haut parfois en bas et certains élèves, parce qu’ils ont des choix dans la stratégie de l’utilisation du cache transposent ces choix sur la file de boîtes.

2) Il est possible aussi que l’élève ait été influencé par le sens de l’écriture de l’accolade, mais aussi la lecture des paquets de 10 sur la file de boîtes.
La recherche du résultat est l’occasion de mettre en œuvre à nouveau du calcul réfléchi sur des petits nombres.

S1c. Seconde méthode, en reculant

Sur la file de dessous, l’enseignant demande une autre façon de faire. Cela va permettre de mettre en évidence, par un résultat identique, l’équivalence des procédures : dans les deux cas, les enfants vont rayer et ils visualisent le résultat.
Le second élève raye les boites en reculant, en commençant par les boîtes pleines : il dit « je raye »les quarante« , je raye »les trente", puis il termine par rayer 9 cases sur la première boite.
Pour le résultat, son organisation en boîtes pleines favorise un calcul rapide (1 et 6) sans comptage ni surcomptage.
Il est important de laisser les élèves effectuer des procédures personnelles qui renforcent les équivalences.

Remarque : on notera que l’enfant au départ est dans une démarche opératoire qui consiste essentiellement à rayer puisqu’il s’excuse presque de faire « un peu la même chose ». On retrouvera le même élève dans une même démarche en fin de séance (S1j).
On voit bien encore ici que c’est le rôle du maître d’extraire du geste (connaissance opératoire) le sens arithmétique (connaissance prédicative) qu’il véhicule.

S1d. Premier bilan de la phase collective

Pour comparer les deux résultats, les élèves privilégient non pas la vitesse d’exécution, mais la facilité à visualiser le résultat d’un seul tenant (connexité des boîtes). Vers 30 s une élève dit : « on voit bien le 7 parce qu’ils sont tous reliés ensemble ».
On notera que l’enseignant, centré sur la méthode en avançant qui est l’objectif de la séance, interprète cette connexité du résultat comme celle des 39 cases à rayer, alors que celles de dessous sont aussi ensemble.
Compte tenu de la seconde méthode utilisée (procédure personnelle efficace), la connexité du résultat de la première favorise cette procédure, ce qui est l’objectif de ce premier bilan.

Ce premier bilan est incomplet :
– Il aurait fallu insister sur l’équivalence des procédures en terme de résultat, même si l’une est perçue comme plus simple que l’autre, ce qui est aussi l’objectif de cette séance.
– La seconde procédure (qui, à terme restera une procédure personnelle) montre une intelligence du calcul s’appuyant sur la représentation des nombres.

S1e. Second exemple pour opérationnaliser la méthode « en avançant »

Ce second exemple (68 - 54) doit permettre d’installer la démarche en avançant. C’est pour cela que le maître prononce cette phrase « où est le 54 ? » qui, de fait, va induire chez l’élève une procédure en avançant.
On peut d’ailleurs remarquer que la relation forte au 54 et la procédure en avançant montre, en creux, que l’équivalence entre les procédures n’est probablement pas acquise à ce moment, ce qui est normal vu la nouveauté du procédé. On notera aussi que le sens de l’écriture, la façon de faire l’accolade, favorise cette procédure en avançant.

En fait de nombreux gestes (bras du maître vers la droite) et la formulation orale (« cinquante et encore quatre » qui s’appuie sur le repère du 50) participent à une institutionnalisation implicite de cette procédure.
Pour trouver le résultat, la prégnance de deux repères successifs à 5, en gras, va aider à visualiser un groupement de 10 (« je peux voir que là ça fait déjà 10 » à 2 min 55 s) et les quantités à droite et à gauche de ce groupement.

S1f. Institutionnalisation de la flèche en avançant

L’utilisation de la flèche montre d’une part qu’on fait le calcul en avançant. D’autre part, on prépare l’élève à établir une équivalence entre l’écart entre les nombres 54 et 68 et le résultat de la soustraction 68 - 54.

Quand on sera sur la droite numérique, le calcul se fera par bonds successifs, en passant par le complément à la dizaine supérieure, le repère des dizaines et le complément au nombre. On voit ici que, sur un repère qui n’est pas calqué sur les dizaines (2 repères à 5) l’élève entreprend la même démarche dans une organisation qui lui est propre : le paquet de 10, les nombres avant et après. C’est aussi du calcul réfléchi sur la file de boîtes.

S1g. Premiers travaux d’élèves

Nous sommes ici dans une première phase d’entraînement. Il est important de souligner la similitude entre l’affichage collectif et le document d’entraînement. On notera que les groupements de 10 sont beaucoup plus visibles que sur le matériel collectif. Le fait que les cases ne soient pas carrées (pour mettre une « bille de Picbille » n’a pas eu d’incidence : les élèves travaillent bien sur des symboles déjà arithmétisés des boites de Picbille.

Ces premiers travaux d’élèves sont l’occasion de mentionner un point important sur la pertinente du matériel utilisé : on raye les cases pour enlever des billes des boites de Picbille, et donc naturellement (après avoir vu le maître faire), les élèves adoptent tous le fait de marquer le premier nombre jusqu’au bord droit de la case (et non pas au milieu comme cela pourrait se rencontrer dans d’autres contextes) car on prend la bille de Picbille.

Ce point, non trivial, est important pour le passage à la droite numérique où le nombre 61 va passer de la représentation de 61 cases (actuellement) à l’abscisse d’un point numérotée 61. Brissiaud appelle ce passage la « ponctualisation des grandeurs ». C’est une difficulté majeure dans la scolarité qu’on retrouvera avec les fractions au cycle 3.

S1h. Deuxième travaux d’élèves

Dans cet extrait, il s’agit de calculer 100 - 87. On voit différentes procédures d’élèves.

Tout d’abord une procédure personnelle qui consiste à ne pas marquer le 100 par une accolade. Ensuite, sur la recherche du résultat on voit bien la différence entre les élèves entrés dans le calcul et ceux qui restent dans le confort du comptage.

S1i. Troisième exemple

Le premier élève tire parti de ses connaissances numériques pour donner rapidement le résultat. D’une manière générale, ce calcul est plus simple pour les élèves que les précédents de par les appuis à 5 et 10.

Vers 1 min 40 s, la fin de l’extrait montre un calcul « en reculant » à partir du nombre de départ — ce qui n’a jamais été fait dans la séance — car c’est une dizaine entière (60) : l’élève se donne une liberté dans les procédures employées qui va inciter le maître à lui demander « une autre façon » (extrait suivant).

S1j. Exemple de non interprétation d’une question conceptuelle

Voulant montrer l’équivalence entre deux procédures, le maître a cette phrase qui se veut conceptuelle (on attend un calcul en avançant) : « peux-tu les rayer autrement ? ».

L’élève n’étant pas dans cette démarche conceptuelle interprète le « rayer d’une autre façon » par une demande de changement de forme tout en s’exécutant « du côté » attendu (peut-être à cause du geste de gauche à droite qui accompagnait la question).

L’élève dessine alors des croix non pertinentes car elles sont les premiers 5 pour rayer des dizaines aussi bien que le dernier 5, ce qui amène le maître à proposer le tracé attendu que l’élève interprète ensuite correctement.

S2a. Extraits de soustraction par visualisation mentale de constellations organisées

La séance débute, comme toujours, par un entraînement au calcul mental sur les petits nombres (avec visualisation mentale par reconstitution de la vision d’autrui). Nous sommes sur une soustraction délicate (15 - 7) car on enlève un nombre proche de la moitié du nombre initial (bascule de la procédure sur le cache). La plupart des élèves trouvent le résultat. Le maître interroge alors un élève qui a produit un résultat faux et qui, cependant, explicite correctement une stratégie de calcul efficace (« moins 7 on enlève 5 et 2 et c’est égal à 8, euh 7 ») : même si le résultat final est erroné, la procédure est experte.

Lors de la correction, les étapes du calcul sont oralisées par une verbalisation fine s’accompagnant d’un geste qui sépare bien le 5 du 2 dans le retrait de 7. Malgré cela, un autre élève propose une verbalisation personnelle encore plus fine qui met l’accent sur le 10 intermédiaire.

S2b. Réactivation de la méthode utilisée

L’argument de rapidité active les connaissances numériques dans la construction du 68 qui elles-mêmes induisent la démarche de calcul en avançant.

S2c. Passage à la droite numérique

Cette séance intervient une semaine après celle de présentation de la méthode avec les files de boîtes. Entre-temps l’enseignante titulaire de la classe a abordé le passage à la droite numérique (que nous n’avons pas filmé pour des questions de disponibilité).

Le passage à la droite numérique est l’abstraction ultime de la file de boîtes de Picbille. Et ce passage de la file de boîtes (avec les billes schématisées par des cases) à la droite numérique, par le travail du calcul en avançant, participe de l’installation de la soustraction comme résultat de la recherche de l’écart entre deux nombres : dans la séance précédente la référence aux cases était explicite dans le calcul final de la différence (« il y en a dix ici, une avant, trois après » par exemple). Cela permettait au final de visualiser l’écart. Dans cette séance, on veut passer à des arguments purement numériques, qui s’appuient sur la connaissance des nombres : recherche des dizaines entières en jeu, complément à la dizaine supérieure...

Subtilement, on conserve un souvenir de la cardinalité des cases par le geste physique de l’accolade que l’on construit au dessus de la droite numérique. L’ordinalité et la cardinalité sont à nouveau intimement liées dans cette activité. Du côté du maître ce lien est vu comme un support de compréhension possible (changement de cadre) ce qui peut ne pas être du tout le cas chez l’élève.

L’élève au tableau a en charge la réactivation de la procédure experte enseignée par la titulaire sur un exemple qui vient d’être traité sur la file des boîtes, ce qui permet d’établir un lien visuel entre les deux supports et les deux procédures : les accolades sur la droites numérique sont liées seulement au calcul du résultat final, le positionnement des deux nombres remplace les deux tracés sur les boites de Picbille. Ainsi, le positionnement du premier nombre (68) est vu de manière ordinale tout en traduisant la cardinalité du nombre de cases rayées. De même le positionnement du second nombre (74) représente aussi le nombre de cases de la première accolade dans la méthode précédente.

Pour établir ces liens porteurs de sens sur les nombres, il est important que les premiers passages à la droite numérique soient accompagnés de la même activité sur la file de boîtes : d’un « calcul sur les objets » on passe à un calcul numérique. On notera que l’enseignant, après le calcul sur la droite numérique, fait un retour sur la file de boîtes pour consolider ce lien.

S2d. Travaux d’élèves sur la soustraction avec la droite numérique

Ces premiers travaux d’élèves traduisent une certaine aisance dans la mise en œuvre de la démarche : le passage de la file de boîtes à la droite numérique semble avoir fonctionné correctement.

On peut remarquer que les compétences géométriques sont essentiellement affines en fin de cycle 2, il est donc normal que les élèves n’aient pas le souci de respecter les proportions, même si certains élèves paraissent sensibles à cette question.
De même, la présence de carreaux sur le cahier de brouillon va induire chez certains des dysfonctionnements passagers comme on va le voir dans un autre extrait.

L’extrait est un peu long car il y a plusieurs passages en temps réel dont Julien (de 42 s à 2 min 33 s) qui a été conservé, car il décrit correctement la procédure qu’il utilise.

S2e. Autres travaux d’élèves sur la droite numérique

Le début de l’extrait est centré sur un élève, d’habitude très à l’aise en calcul mental, qui focalise sur le complément à la dizaine supérieure : « de 76 à 80, il y a 4 et de 90 à 88 il y a 2 », à tel point qu’une description de 88 en « 80 + 8 » n’induit pas de relation à l’accolade entre 80 et 88 : à ce moment-là de la séance, pour cet élève, le lien entre cardinalité et ordinalité ne fonctionne pas, alors même que l’oralisation de 88 contient la décomposition en 80 et 8.

Pour certains élèves (à 2 min 40 s) on propose une activité différenciée en revenant à la file de boites. Vers 3 min, une autre élève fait la même erreur sur le 88 : « de 80 à 88 il y a combien ? ». Réponse « 2 », avant une correction laborieuse.

Ces deux exemples montrent à quel point la traduction en composition additive des grands nombres, y compris dans la zone de régularité orale des 80 reste encore fragile et que la cardinalité associée n’est pas encore acquise.

C’est important pour nous de rappeler que le travail sur la numération au CP doit s’appuyer sur un matériel qui doit figurer les groupements de 10.

S2f. Correction par un élève

La correction au tableau met en évidence le passage par la dizaine supérieure. Le calcul final est l’occasion d’un rappel sur une stratégie de calcul passant par la dizaine supérieure : 8 + 4 = (8 + 2) + 2.

S2g. Calcul réfléchi de la soustraction mobilisant deux dizaines intermédiaires

L’enseignant propose le calcul réfléchi de la soustraction 87 - 66 en précisant qu’il y a une difficulté supplémentaire. Comme on le voit au début de l’extrait (autour de 1 min), certains élèves n’éprouvent aucune difficulté à positionner les deux dizaines intermédiaires et à trouver le résultat rapidement.

Vers 1 min 50 s l’enseignant utilise l’analogie de la grenouille pour autoriser les élèves à effectuer plusieurs étapes dans le calcul.
À partir de 2 min 30 s on s’intéresse à un élève qui a plus de difficulté à intercaler les deux dizaines entières et qui, pour cela (à 2 min 50 s) prend appui sur la bande numérique collective affichée dans la classe. Cette étape étant réalisée, le calcul final est l’occasion d’activer des procédures de calcul réfléchi pour éviter le surcomptage (en particulier pour 17 + 4).

On voit dans ces extraits que le confort et la sécurité du comptage nécessitent, de la part des enseignants, une vigilance et une réactivation constante du calcul.

S2h. Correction de la soustraction précédente

Comme il s’agit de la dernière soustraction « en avançant » de la séance, cette correction est l’occasion de rappeler les différentes étapes permettant d’accéder au résultat.
Comme l’élève place naturellement les deux dizaines intermédiaires, l’enseignant sollicite les élèves ayant des difficultés et, en particulier, celui qui a utilisé la frise numérique collective (à 35 s).

L’obtention du résultat final (à partir de 1 min 30 s) est l’occasion d’un vrai calcul de la part de l’élève.

S2i. Retour à la soustraction en reculant

Dans une deuxième partie de la séance, on souhaite voir comment les élèves vont aborder la soustraction dans le cas où on retire peu (74 - 6). Pour cela, l’enseignant redistribue de feuilles figurant les files de boites de Picbille.

À 34 s, un élève donne spontanément le résultat. Il le justifie vers 1 min par un procédé personnel un peu complexe (6 = 5 + 1 donc 4 + 1 + 1) et revendique l’efficacité de sa procédure personnelle par un « je préfère, c’est ma façon de faire ».

S2j. Décomptage et soustraction en reculant

Après une première élève qui semble décompter sur la file de boîtes, vers 22 s, un élève verbalise sa procédure de recul sur la frise « pour éviter de compter ». Puis il lit le résultat en s’appuyant sur les dizaines : 60, puis 5 et 3.

On a associé ces deux exemples pour monter la différence entre un décomptage sur la frise, qui n’entre pas dans le domaine arithmétique et un recul sur la frise qui, pour exprimer le résultat final, mobilise toutes les connaissances en numération.

S2k. Mise en commun sur la soustraction en reculant

Une première élève prend le contre-pied de l’objectif du maître en proposant un calcul en avançant et surtout en exécutant ce calcul très rapidement. La visualisation des boîtes de dix est certainement à l’origine de cette rapidité un peu surprenante.

L’enseignant profite de ce choix imprévu pour mettre en évidence l’équivalence des deux procédures en demandant à un élève d’effectuer une autre façon de faire (à 1 min 22 s). En partant de 74 et en proposant de barrer « quatre et deux », l’élève, dans son geste, matérialise l’étape du passage à 70, et donc rend visible à la classe son propre calcul réfléchi.

Devant la rapidité de la démarche de l’élève, le maître illustre et verbalise les différences de cette démarche. C’est l’occasion de montrer que, même si c’est à l’opposé de sa propre démarche, l’enseignant est parfois obligé de recourir à ce qu’il veut éviter : ici du décomptage partiel pour accrocher des élèves fatigués. En effet, l’objectif était d’arriver à montrer que les deux élèves trouvent le même résultat, et donc que les procédures sont équivalentes.

Sur ce support, il est difficile de statuer sur la pertinence d’une méthode par rapport à l’autre. Le choix pertinent (en reculant pour cet exemple) s’imposera en passant à la droite numérique.