L’indice de masse corporelle, ou IMC, d’une personne adulte, est défini comme le quotient de sa masse, en kilogrammes, par le carré de sa taille, en mètres. Il s’agit d’une notion statistique inventée par Adolphe Quételet au 19^e siècle.

Dans tout cet article, on considèrera le cas de Monsieur B. H. O., ancien basketteur, qui mesure un bon mètre 86 pour 72 kilos, ce qui lui confère un IMC de $\frac{72}{1,86^2}\simeq 21$ : Bonne nouvelle pour lui, Monsieur B. H. O. est en bonne santé avec un IMC normal.

Abaques

Pour calculer graphiquement l’image d’un nombre par une fonction, on repère l’antécédent sur l’axe des abscisses grâce à des graduations portées sur celui-ci, puis on utilise la représentation graphique de la fonction pour repérer $f(x)$ sur les graduations de l’axe des ordonnées. Cette activité est une part importante du programme de maths au lycée, comme en témoigne le nombre de sujets — par exemple du bac STG — portant sur la question.

Le même procédé permettrait de calculer graphiquement $f(x,y)$ en repérant $x$ et $y$ sur deux axes puis en utilisant la représentation graphique de $f(x,y)$ pour situer le nombre cherché sur un troisième axe gradué, avec cette différence importante que la représentation graphique est une surface, ce qui rend l’exercice un peu plus difficile, et se fait maintenant dans l’espace tridimensionnel.

Dans le cas présent, la fonction donnant l’IMC est $f(x,y)=\frac{x}{y^2}$ dont la représentation est une surface cubique (par produit en croix on a $zy^2=x$) dont l’outil Polyray de WIMS donne la représentation suivante :

Pour utiliser cette surface, on mène le point de l’axe des abscisses jusqu’à la graduation 1,86 (graduation non représentée ci-dessous) et le point sur l’axe des ordonnées sur la graduation 72, puis on regarde le point de la surface à la verticale du point de coordonnées (1,86 ; 72 ; 0). Par définition, sa cote (ou hauteur) est l’IMC de Monsieur B. H. O. qui se lit alors sur l’axe des cotes (graduations non représentées ci-dessous non plus, pour ne pas trop surcharger la figure). On peut regarder la scène sous plusieurs angles en utilisant le cliquer-droit-glisser de la souris :

Finalement l’angle le plus pratique pour regarder cette scène, c’est d’au-dessus, car dans ce cas on a un dessin plan, mais pour lire la hauteur du point d’abscisse 1,86 et d’ordonnée 72, on ne peut plus utiliser les graduations de l’axe des $z$ puisqu’on ne voit plus celui-ci, mais les lignes de niveau de la surface précédente. Alors on repère 1,86 sur l’axe des abscisses et 72 sur l’axe des ordonnées [1], puis on regarde la courbe (ce sont des paraboles) la plus proche du point obtenu, et on y lit l’IMC de Monsieur B. H. O. qui est toujours 21 :

La ressemblance avec ce tableau explique l’étymologie du mot abaque. Le fait que chaque zone de catégories d’IMC (normal, trop petit, trop gros) peut être coloriée dans une couleur différente et la rapidité de la construction graphique favorisent ce type de représentation car plus parlante, comparée par exemple à ce beau programme en JavaScript.

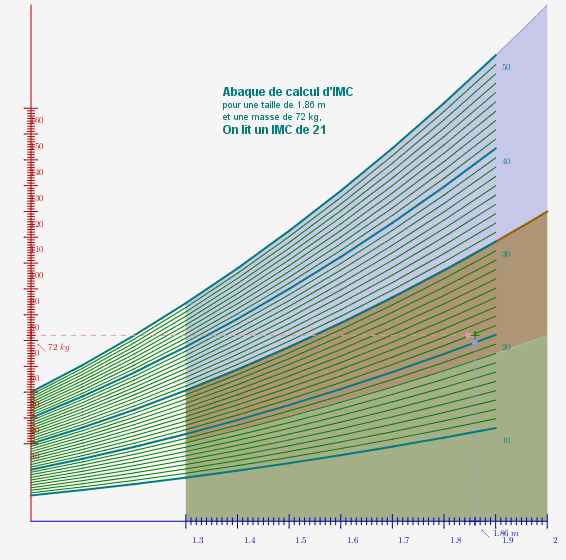
Si maintenant on gradue les axes de coordonnées en graduations logarithmiques, la définition de l’IMC devient $z=x-2y$ qui représente un faisceau de droites, plus faciles à construire et moins tassées que les paraboles précédentes. On a alors l’abaque suivant, qui s’utilise de la même manière que le précédent :

Cependant l’abondance de courbes, ou de droites, rend difficile la lecture de ce genre d’abaques. En utilisant la notion de dualité en géométrie projective, Maurice d’Ocagne a transformé ces abaques en ce qu’il a baptisé nomogrammes avec son système de coordonnées parallèles et dont on ne montre que deux exemples ci-dessous :

Nomogrammes

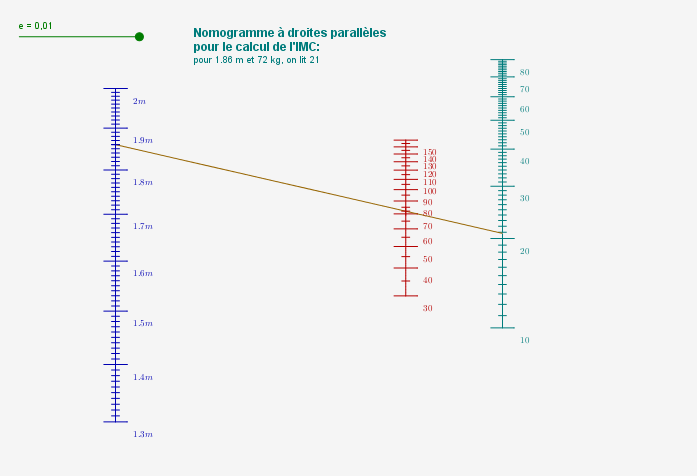
La duale de la figure précédente est formée de trois droites parallèles :

On repère les 1,86 mètres et 72 kilos sur les deux premières droites, et on mène par ces graduations une droite [2], qui coupe la troisième droite parallèle en un point correspondant à la graduation 21 : L’IMC de Monsieur B. H. O. est donc de 21.

Dans le cas des nomogrammes, les zones correspondant aux différentes catégories d’IMC sont des segments, non coloriés ci-dessous. Le coloriage a été fait sur le nomogramme ci-dessous basé sur deux arcs de paraboles gradués, l’un par la taille, l’autre par l’IMC, et une droite graduée par la masse :

En déplaçant le point bleu sur la graduation 1,86 et le point cyan sur la graduation 72, la droite formée par ces deux points coupe l’arc de parabole des IMC sur la graduation 21, ce qui confirme que l’IMC de Monsieur B. H. O. est bien 21.