Qu’est-ce qu’un booléen ?
C’est une variable qui ne peux prendre que deux valeurs : VRAI ou FAUX.
En Python, le type d’une telle variable est bool, les deux valeurs possibles sont True ou False.
Expressions booléennes
Une expression booléenne a deux valeurs possibles : True ou False.
Python attribue à une expression booléenne la valeur False si c’est :
– la constante False
– la constante None
– une séquence ou une collection vide
– une donnée numérique de valeur 0. Tout le reste vaut True.
>>> type(False)
<class 'bool'>
>>> type(True)
<class 'bool'>
>>> False
False
>>> bool(None)
False
>>> bool(' ')
True
>>> bool('')
False
>>> bool(0)
False
>>> bool(156.87)
TrueOpérateurs relationnels ou de comparaison
Ce sont les opérateurs == , != , > , >= , < et <=.
* Illustration pour x = 7 et y = 17
| Opérateur | Expression | Signification | Valeur |
| == | x == y | Égal | 0 (faux) |
| != | x != y | Non égal | 1 (vrai) |
| > | x > y | Plus grand que | 0 |
| < | x < y | Plus petit que | 1 |
| >= | x >= y | Plus grand ou égal à | 0 |
| <= | x <= y | Plus petit ou égal à | 1 |
| is | x is y | est le même objet | 0 |
| is not | x is not y | n’est pas le même objet | 1 |
Cela donne dans le shell de Python :
>>> x=7
>>> y=17
>>> x==y
False
>>> x!=y
True
>>> x>y
False
>>> x>=y
False
>>> x<y
True
>>> x<=y
True
>>> x is y
False
>>> x is not y
True
* Illustration avec deux chaînes de caractères
>>>a='encyclopédie1'
>>>b='encyclopédie2'
>>>a==b
False
>>>len(a)
13
>>>a[:12]==b[:12]
TrueExercices Python
1/ Écrire un programme dont la sortie dans le shell de Python est la suivante :
>>>Entrez un entier naturel : 45
>>>Entrez un second entier naturel : 215
>>>
>>> x==y a pour type <class 'bool'>
>>>
>>> x==y est un booléen : il est soit vrai, soit faux
>>>
>>>x est différent de y donc la valeur du booléen est : False2/ Écrire un programme qui dira si
– un nombre x appartient à l’intervalle [a, b]
– un nombre x appartient à l’intervalle ]a, b[ U [c, d]
– un nombre x appartient à l’intervalle [a, b[ ∩ ]c, d]
3/ Écrire un programme qui affiche Bon anniversaire ! si nous sommes à la date de votre anniversaire, Bonne journée sinon.
Les 3 opérateurs logiques
Les expressions avec un opérateur logique sont évaluées à True ou False.
* Le NON (négation, contraire)
p étant un booléen,
NON p = 1 - p
En Python, on appelle l’instruction not.
(NON p est noté en logique ¬p)
>>> 2<1
False
>>> not 2<1
TrueTable de vérité : retrouver celle de NON p à l’aide de Python.
| p | NON p | |
| VRAI | FAUX | |
| FAUX | VRAI |
Correction en Python :
>>> P=[True,False]
>>> for p in P:
print(p,not p)
True False
False True
* Le OU logique (disjonction)
p et q étant deux booléens,
p or q
vaut True si p vaut True. Si p est False, l’expression est évaluée à la valeur booléenne de q
(si p est faux, retourne q, sinon retourne p).
(p OU q est noté en logique p ∨ q)
>>> 8<9
True
>>> 2<1
False
>>> (8 < 9) or (2 < 1)
TrueRetrouver à l’aide de Python la table de vérité d’une disjonction :
| p | q | p OU q | |
| VRAI | VRAI | VRAI | |
| VRAI | FAUX | VRAI | |
| FAUX | VRAI | VRAI | |
| FAUX | FAUX | FAUX |
* Le ET logique (conjonction)
p and q
vaut False si p est False. Si p est True, l’expression est évaluée à la valeur booléenne de q
(si p est faux, retourne p, sinon retourne q).
(p ET q est noté en logique p ∧ q)
>>> 8<9
True
>>> 2<1
False
>>> (8 < 9) and (2 < 1)
False
>>> x=36
>>> (x > 13) and (x < 27)
False
>>> x=20
>>> (x > 13) and (x < 27)
TrueRetrouver à l’aide de Python la table de vérité d’une conjonction :
| p | q | p ET q | |
| VRAI | VRAI | VRAI | |
| VRAI | FAUX | FAUX | |
| FAUX | VRAI | FAUX | |
| FAUX | FAUX | FAUX |
Aller plus loin en logique : implication, équivalence et ou exclusif
L’implication logique p ⇒ q est le booléen : NON p OU q
– Dresser à l’aide de Python la table de vérité de l’implication logique.
– Écrire une fonction implique(p,q) en Python qui retourne NON p OU q, p et q étant deux booléens.
L’équivalence logique p ⇔ q est le booléen : (p ⇒ q) ET (q ⇒ p)
– Dresser à l’aide de Python la table de vérité de l’équivalence logique.
– Écrire une fonction equivalence(p,q) en Python qui retourne (p ⇒ q) ET (q ⇒ p), p et q étant deux booléens.
* Le OU exclusif (XOR) :
soit p, soit q, mais pas les deux à la fois.
Le OU exclusif (noté XOR ou ⊕) p XOR q est le booléen : (p OU q) ET NON (p ET q).
Retrouver à l’aide de Python la table de vérité du OU exclusif :
| p | q | p XOR p | |
| 0 | 0 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 |
Voir une application en cryptographie
Questions :
– Quel serait le message en français envoyé du futur dans le film « Le code Andromède » s’il était codé à l’aide de la clé de 7 bits K=1001110 et du OU exclusif ? [1]
– Écrire une fonction xor(p,q) en Python qui retourne soit p (sous-entendu p Vrai), soit q (sous-entendu q Vrai) mais pas les deux, p et q étant deux booléens.
Récapitulatif :
Voir sur Wikipédia l’article Fonction logique
Mini-projet
À rendre par groupe.
– Écrire un programme Python qui dresse les tables de vérité de NON p, p OU q, p ET q telles qu’elles sont affichées dans ce tableau :

NONp
|

pOUq
|
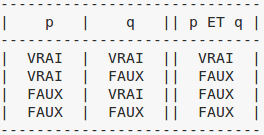
pETq
|
Annexe : formatage d’une chaîne de caractères : lire Apprendre à programmer avec Python3 de Gérard Swinnen page 158 : Formatage des chaînes de caractères.
– Découverte des propriétés de l’Algèbre de Boole
p et q sont deux booléens.
Démontrer à l’aide d’un programme Python que :
- Règles d’addition (le OU est noté +)
p + 0 = p
p + 1 = 1
p + p = p
p + NON p = 1 - Règles de multiplication (le ET est noté . )
p . 0 = 0
p . 1 = p
p . p = p
p . NON p = 0 - Commutativité
p . q = q . p - Associativité
p . ( q + r ) = p . q + p . r
- Les lois de MORGAN
p et q sont deux booléens.
Démontrer à l’aide d’un programme Python que :
NON (p OU q) = NON p ET NON q
NON (p ET q) = NON p OU NON q
- Vérifier que (p ⇒ q) et (NON q ⇒ NON p) ont même table de vérité.
- Tautologie
p, q, r sont trois booléens.
Vérifier que [(p ⇒ q) ET (q ⇒ r)] ⇒ [p ⇒ r] est toujours vrai.
C’est la base des raisonnements en chaîne en mathématiques.


Commentaires