Le combinateur Y de Curry est dit
- paradoxal (pour des raisons exposées plus bas) ;
- ou de point fixe : En effet, si on essaye de l’appliquer à une fonction g (l’œuf saumon), on a successivement :

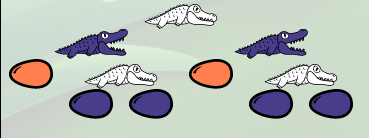

qui peut se résumer en Yg=g(Yg) :
- Yg est un point fixe de g.
- Lequel ?
- Un point fixe.
- Oui mais si g n’a pas de point fixe ?
- Yg est un point fixe de g, puisqu’on vous le dit !
- Même s’il n’y en a pas ?
- Même s’il n’y en a pas.
En fait, grâce à « leq » on peut définir des fonctions pour lesquelles la boucle induite par Y s’arrête, et ceci permet de définir par exemple la factorielle en λ-calcul.
Paradoxe de Curry
| Si cette phrase est vraie, alors 2+2=5 |
On rappelle que la fausseté de a⇒b équivaut à a∧¬b
- Si la phrase ci-dessus était fausse, alors
- elle serait vraie
- (et 2+2 ne serait pas égal à 5)
- Alors qu’elle soit vraie ou fausse, en définitive elle est vraie. Bon, c’est simple finalement, la phrase « si cette phrase est vraie alors 2+2=5 » ne peut pas être fausse, donc elle est vraie.
Oui, mais c’est une implication dont la prémisse est vraie (puisque la prémisse est la phrase même). Donc sa conclusion est vraie aussi : 2+2=5 cqfd
2+2=5 ???
Quoi ? C’est quoi cette histoire ?
Curry peut démontrer que 2+2=5 ?
Ah avec ces expériences nucléaires ils ont tout déréglé les saisons. Où va-t-on Mâme Michu ? Voilà que maintenant 2+2=5...
On l’aura compris, le paradoxe est autoréférentiel et provient du fait que s’il suffit qu’une implication suppose sa propre prémisse pour que la conclusion soit vraie, le résultat est paradoxal chaque fois que la conclusion est fausse, soit dans la moitié des cas.
Maintenant on remarque qu’à un moment du raisonnement ci-dessus, se trouve l’affirmation « si elle n’est pas fausse, c’est qu’elle est vraie ». Le paradoxe de Curry perd donc son caractère paradoxal en logique intuitionniste puisque cette partie du raisonnement est basée sur le principe du tiers exclu qui n’est pas adopté par la logique intuitionniste. Autre boucle autoréférentielle : La logique intuitionniste est de Brouwer, le célèbre auteur du théorème du point fixe : La boucle est bouclée !














Commentaires