Lorsque Dundee arriva dans le pays des alligators cannibales, il commença par vérifier son paquetage puis sans même se reposer, partit pour une exploration des environs. Sitôt qu’il se fût habitué aux moustiques, il découvrit le premier exemplaire d’une famille répandue dans la région :

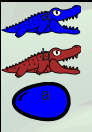
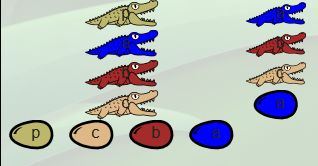
Cette famille est constituée du patriarche, dans une couleur (ici le bleu correspondant au type a), lequel veille sur un juvénile d’une autre couleur que lui (ici, en rouge correspondant au type b) et, via ce juvénile, sur un œuf de même couleur que le patriarche. Dans le jeu, cette famille peut s’obtenir à partir de la console, en cliquant sur « true ». Le langage de script de ce jeu décrit alors la famille par λa.λb.a ou toute autre combinaison de lettres à la place de a et b (du moment que ce sont des lettres différentes. Dundee comprit vite le comportement de la famille true en présence de deux sources de nourriture, par exemple deux œufs de couleurs respectives c et d (expression (λa.λb.a) c d dans le langage de script du jeu) :

L’alligator bleu commence par manger le premier œuf (c) ce qui a deux effets immédiats :

• il meurt d’indigestion et disparaît du tableau
• l’œuf bleu qu’il protégeait subit une mutation et devient un œuf identique à celui qui a été ingéré.

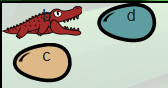
Mais le juvénile, devenu nouveau patriarche, a maintenant accès à la source de nourriture qui reste, l’œuf de type d, et ingère celui-ci, avant de mourir à son tour d’indigestion :

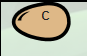
Dans ce cas, il n’y a pas eu de mutation génétique parce que l’ancienne couleur de l’œuf n’est pas la même que la couleur de son protecteur. Plus généralement, lors du décès du patriarche par indigestion, l’œuf que celui-ci gardait indirectement éclot, et produit une famille identique à celle que le patriarche vient d’ingérer. Dundee comprit alors

• qu’en réalité l’œuf ne changeait pas de couleur, mais subissait une éclosion qui révélait son nouveau contenu, qui est un œuf de la nouvelle couleur dans le cas présent
• que face à deux sources de nourriture, une famille de type true laissait toujours une copie de la première après son orgie cannibalistique.

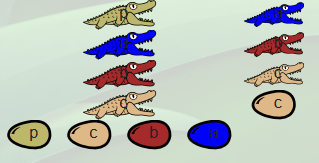
Plus loin, Dundee aperçut une autre famille d’alligators, dans laquelle l’œuf est de la même couleur que le juvénile : La famille false (notée λa.λb.b) :

Son comportement alimentaire n’est pas le même que celui de la famille true, à cause de la couleur de l’œuf que n’est pas la même. Mise en présence de deux œufs de type c et d,

au début il se passe la même chose qu’avec la famille true : L’alligator bleu mange l’œuf de type c et meurt d’indigestion :

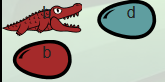
Mais cette fois-ci, comme l’œuf du bas n’est pas de la même couleur que l’ex patriarche, il ne se passe rien à son niveau. Du moins pour l’instant parce qu’une fois que le nouveau patriarche voit son repas, et comme il est de la même couleur que l’œuf qu’il protégeait, celui-ci va, après le décès de son gardien par indigestion, devenir ce que son protecteur a ingéré juste avant indigestion :

Plus généralement, une famille de type false, placée devant deux repas, devient non plus le premier d’entre eux (comme la famille true), mais le second.

Comme Dundee a aperçu ces deux familles d’alligators le premier jour (ou jour 1), au bout de la zone d’exploration, il les a baptisés « les bouts les 1 », anglicisé en « booléens »...

retour en haut des onglets

Le second jour de son exploration, Dundee a découvert une famille d’alligators dans le lac de la négation les Né-gators :

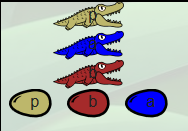
Cette famille a un comportement intéressant lorsqu’elle mange un booléen. Par exemple, située près d’une famille true :

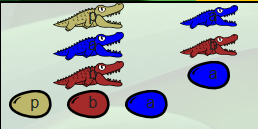
C’est le moment de (re)découvrir une autre règle du jeu : La règle de la couleur. Les alligators sont peut-être cannibales parce qu’il mangent des alligators (ou leurs œufs) mais pas ceux de la même couleur qu’eux. Alors les proies se comportent comme des caméléons qui changent de couleur quand ils ont peur. Ici les a deviennent des c et les b deviennent des d :

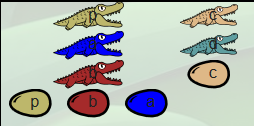
En fait λc.λd.c est autant une description du booléen vrai que λa.λb.a. Alors, l’alligator p dévore, des yeux puis pour de bon, toute la famille vrai qui est devant lui. Ce qui va évidemment le tuer d’indigestion et, comme il surmonte un œuf de la même couleur que lui, cet œuf va éclore et donner naissance à une nouvelle famille true :

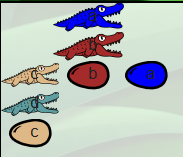
Les alligators adultes ont de plus en plus faim, mais il n’y a plus rien à manger devant eux. Par contre le jeune patriarche qui chapeaute la sous-famille true voit devant lui deux œufs (le b et le a) et mange le premier d’entre eux :

Ses deux gardiens ne pouvant le protéger de l’indigestion, il disparaît à son tour, laissant son protégé l’alligator d devant un œuf appétissant, qu’il dévore à son tour, avant de disparaître. Comme il ne surplombe aucun œuf de sa propre couleur, tout finit à ce point :

Ainsi, Dundee note dans son carnet ce fait intéressant :

Mais l’histoire ne s’arrête pas là : Lorsque la même famille né-gator mange une famille false il en résulte une famille true selon les étapes suivantes (extraits du carnet d’esquisses de Dundee) :

Les deux familles côte à côte :

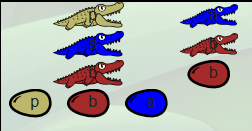
La même situation après renommage des éléments de la famille false (λa.λb.b devenu λc.λd.c) :

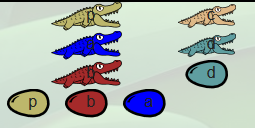
Puis après l’ingestion-indigestion par l’alligator p, de la famille false, et éclosion de l’œuf de la même couleur :

Après le repas-suicide de l’alligator c :

Puis celui de l’alligator d :

Effectivement le résultat final est une famille vrai. Ainsi, cette famille opère sur un booléen en le transformant en l’autre booléen, exactement comme le fait la négation en logique propositionnelle [3].

retour en haut des onglets

Dans la console du jeu, en cliquant sur « And » on voit λp.λq.p q p qui donne cette famille :

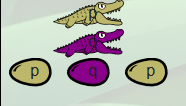
Elle est plus vorace que la famille né-gator, puisqu’elle mange deux booléens (l’un après l’autre). Par exemple, face à deux familles ( une true et une false, données par (λp.λq.p q p) (λa.λb.a) (λc.λd.d)) :

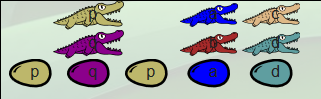
Comme d’habitude, l’alligator p est le premier à passer à table (et à disparaître). Les œufs qui portent sa couleur vont donc éclore en donnant naissance à deux familles true au complet :

L’alligator mauve va alors manger la famille false de droite, qui est la seule à sa portée. Il disparaît et l’œuf mauve éclot en donnant naissance à une nouvelle famille false :

On a alors une situation rare : Trois familles booléennes côte à côte (true, false, true). C’est la première qui va se régaler, d’abord en laissant son patriarche dévorer la famille false (ce qui fait naître une autre famille false placée sous sa protection) :

Puis en laissant le juvénile avaler la famille true restante :

Le résultat, stable, est une famille booléenne : Une famille false [4] λc.λd.d

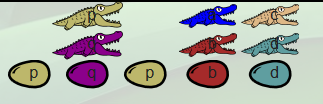
Ainsi, la famille and avale deux booléens et produit un booléen : C’est une opération. Dundee a consigné dans son carnet les résultats possibles :

situation de départ	résultat produit

C’est la version crocodilienne de la table de vérité de la conjonction, cette famille d’alligators implémente donc la conjonction booléenne...

La famille or (ou inclusif) ressemble à la famille and (onglet précédent). Pas étonnant puisqu’il s’agit là aussi d’un opérateur booléen :

Elle va donc elle aussi manger deux familles booléennes, comme par exemple une famile true et une famile false (script (λp.λq.p p q) (λa.λb.a) (λc.λd.d) après avoir renommé les variables de la famille false en c et d) :

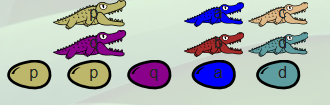
Mais cette fois-ci, après le repas crocodilo-cannibalistique, il reste cette famille :

Ce n’est pas une famille false comme en laissait l’opérateur and, mais une famille true reconnaissable à ce que l’œuf est de la même couleur que le patriarche et non celle du juvénile.

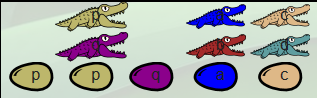
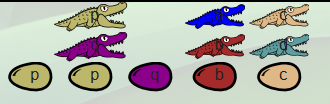
Après avoir passé quelques jours à se faire piquer par les moustiques étudier cette famille et ses mœurs alimentaires, Dundee a noté ceci dans son carnet :

situation de départ	restes des repas

On reconnaît là, la table de vérité de la disjonction inclusive, qui est donc représentée par cette famille.

Une expression représentant la disjonction exclusive est

(λm.λn.  m  ( (λp.λa.λb.p b a) n) n))

Voici cette famille, telle que découverte par Dundee :

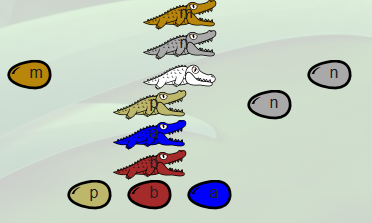
Et voici ce que Dundee a noté dans son carnet, sur cet opérateur :

situation avant repas	restes

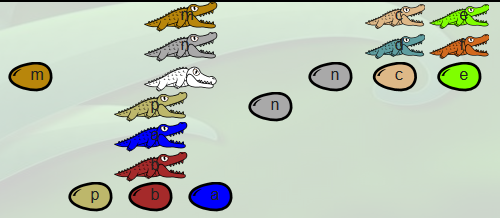
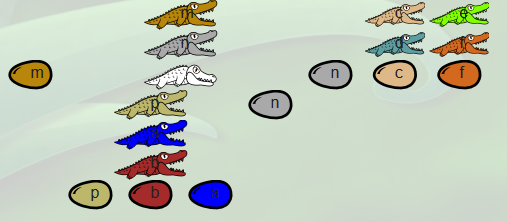
On reconnaît la table de vérité du ou exclusif.

retour en haut des onglets

En définissant m⇒n comme ¬m∨n, on a la λ-expression suivante :

λm.λn ((λp.λq.p p q)( (λp.λa.λb.p b a) m) n)

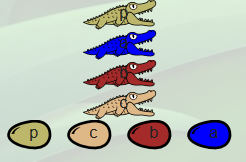
La famille représentée est celle-ci [5] :

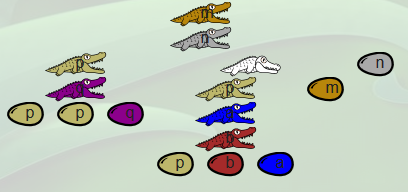
Dundee s’est beaucoup impliqué dans l’observation de cette famille, et voici ses carnets :

situation avant repas	restes des repas

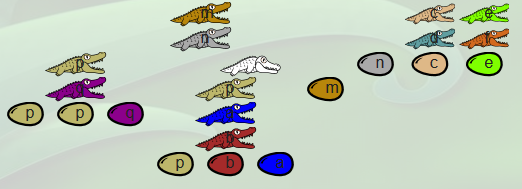
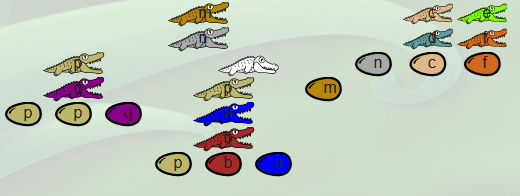
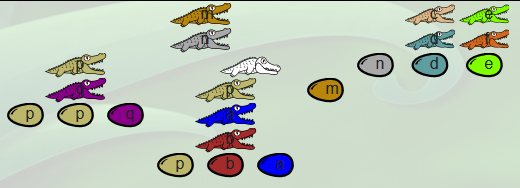
Avec l’interpréteur CoffeeScript ci-joint, on peut tester le script suivant :

affichage = (booleen) -> 
    booleen "2+2=4", "2+2=5"
vrai = (a,b) -> a
faux = (a,b) -> b
leContraireDe = (booleen) -> 
    (a,b) -> booleen b, a
laDisjonctionDe = (a,b) ->
    b b, a

implication = (a,b) -> 
    laDisjonctionDe (leContraireDe a), b

alert affichage implication vrai, vrai
alert affichage implication vrai, faux
alert affichage implication faux, vrai
alert affichage implication faux, faux

En fait, toute opération logique peut se définir à partir des opérations de base suivantes :

• la négation
• la conjonction
• la disjonction inclusive [6]

Mais à partir de la négation et l’implication aussi on peut définir les autres opérations logiques. Par exemple on peut définir la disjonction p∨q comme ¬p⇒q. On peut même définir la négation à partir de l’implication, ¬p étant un synonyme de p⇒⊥.

retour en haut des onglets