Description
Dans les années 1950, Carl Adam Petri, alors lycéen, a inventé ce genre de diagrammes pour résoudre des problèmes de stœchiométrie :
Il s’est servi de ces diagrammes lors de son travail de thèse, titré communication avec des automates : c’est d’informatique qu’il s’agit. La notion de réseau de Petri est très présente dans les travaux d’informatique portant sur des problèmes d’indécidabilité, notamment avec la notion d’interblocage. Ces objets sont suffisamment abstraits pour qu’on ait envie d’expérimenter leur découverte par la manipulation voire par l’enseignement kinesthésique.
Addition
Ce réseau de Petri a une particularité : chacune de ses deux transitions a exactement une entrée et une sortie, et ne fait donc transiter qu’un seul jeton à la fois. Par exemple si la première place (en haut à gauche) contient 3 jetons et que la seconde place (en bas à gauche) contient 2 jetons :
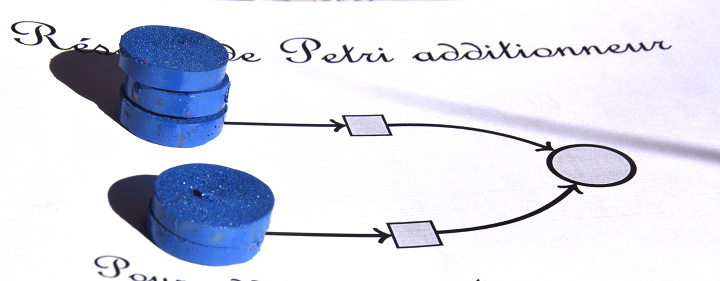
il est possible dans un premier temps de faire transiter un des 5 jetons vers la place de droite, en déclenchant une des deux transitions. Par exemple celle du haut :

Après on peut déclencher la même transition, ou l’autre, sans que cela influe sur le résultat final qui est celui-ci :
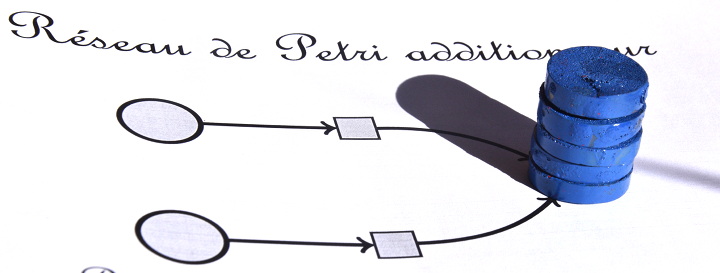
En fait, en notant h la transition du haut et b celle du bas, on peut avoir n’importe lequel de ces historiques :
bbhhh
bhbhh
bhhbh
bhhhb
hbbhh
hbhbh
hbhhb
hhbbh
hhbhb
hhhbbque l’on peut résumer en « la transition du haut a été activée exactement 3 fois et celle du bas, exactement 2 fois, dans n’importe quel ordre ». Dans tous les cas, le résultat final est que les 5 jetons sont groupés dans la place de droite : ce réseau de Petri a effectué l’addition 3+2=5.
Comme l’ordre dans lequel s’effectuent les transitions n’a pas d’influence sur le résultat, chacune des 10 histoires possibles est résumée dans un unique vecteur commutatif écrit (3,2). D’autres vecteurs seront vus dans les onglets suivants.
Duplication
Dans ce réseau de Petri, il n’y a qu’une transition, mais chaque fois qu’elle absorbe un jeton, elle en envoie 2, un dans chacune de ses places de destination.
Par exemple si au début il y a 3 jetons dans la place de départ (à gauche) :

à chaque fois qu’un des trois jetons est absorbé par la transition, un jeton apparaît dans chacune des deux places d’arrivée, ce qui fait qu’à la fin on a :

Ce réseau de Petri duplique donc (dans les deux places d’arrivée) les jetons qui étaient dans la place de départ.
Comme le réseau comporte 3 places, on peut représenter son état par un vecteur de dimension 3. En appelant z le nombre de jetons de la place de gauche, x et y les nombres de jetons des places en haut à droite, et en bas à droite, l’état initial est
(0,0,3)
et à chaque déclenchement d’une transition, l’état change, de la façon suivante :
(1,1,2)
(2,2,1)
(3,3,0) (état final)En fait, pour passer d’un état au suivant, on applique une translation dont le vecteur est
| 1 |
| 1 |
| -1 |
Ce modèle (additionner un vecteur tant qu’on peut le faire) s’appelle un VAS (« vector addition system » ou système d’addition de vecteurs). En effet sur certains réseaux de Petri, il y a plusieurs vecteurs possibles à additionner. Par exemple le réseau de Petri additionneur de l’onglet précédent a deux transitions, chacune avec son vecteur. Le VAS correspondant est
| -1 | 0 |
| 0 | -1 |
| 1 | 1 |
On concatène les deux vecteurs et le résultat (ci-dessus) est la matrice d’incidence du réseau de Petri. Comme le montre l’exemple ci-dessus
- le nombre de colonnes de la matrice est le nombre de transitions du réseau de Petri
- le nombre de lignes de la matrice est le nombre de places du réseau de Petri.
En fait, si on multiplie la matrice d’incidence par le vecteur commutatif (3,2), on obtient le vecteur (-3,-2,5) qui est précisément celui qu’on ajoute au vecteur intial (3,2,0) pour avoir le vecteur final (0,0,5). Ce résultat se généralise : le calcul matriciel permet de trouver rapidement l’état final d’un réseau de Petri. C’est comme si on remplaçait une suite de franchissements par un franchissement unique.
Multiplication par 2 ou 3
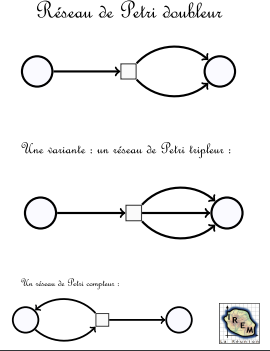
En assemblant en une seule place, les deux places du duplicateur, on obtient un réseau de Petri doubleur (ou multiplicateur par 2) :
Par exemple si au début on a 2 jetons dans la place de départ :

à la fin on en aura 4 (soit le double) dans la place d’arrivée :

Le réseau de Petri ne comportant qu’une transition, sa matrice d’incidence est donc un vecteur, cette fois-ci en dimension 2 :
| -1 |
| 2 |
Les états successifs du VAS sont les suivants :
(2,0) (état initial)
(1,2)
(0,4) (état final)En calculant le double du nombre de jetons sur la place de départ, additionné au nombre de jetons sur la place d’arrivée, on constate que
- 2×2+0=4
- 1×2+2=2+2=4
- 0×2+4=4
Cette quantité reste constante au cours de l’évolution du réseau de Petri : c’est un invariant du réseau. En appelant x et y les quantités de jetons sur les deux places, on a 2x+y=4 et la quantité 2x+y est invariante.
Un autre réseau (avec un arc de plus) effectue le triplement. Avec 2 jetons dans la place de départ au début :

on se retrouve avec le triple de 2 (soit 6 jetons) dans la place d’arrivée à la fin :

Le vecteur d’incidence de ce réseau de Petri est
| -1 |
| 3 |
Et la quantité 3x+y est invariante :
(2,0) 3×2+1×0=6 (état initial)
(1,3) 3×1+1×3=6
(0,6) 3×0+1×6=6 (état final)Ce réseau de Petri possédant un invariant, il est borné, c’est-à-dire que jamais le total des jetons ne dépassera 6 : il y en a successivement 2, puis 4, puis 6. En fait comme 3x+y=6, on a x+y=6-2x : la quantité totale de jetons est bornée par 6.
Pour le réseau de Petri duplicateur, x+y+2z est invariant et le réseau de Petri duplicateur est également borné. Pour le réseau de Petri additionneur, c’est x+y+z qui est invariant : la quantité totale de jetons est invariante sur ce réseau.
Division par 2
En inversant les flèches sur le réseau de Petri doubleur, on obtient un réseau de Petri diviseur par 2 :
Par exemple pour effectuer la division de 6 par 2, on commence par placer 6 jetons dans la place de gauche :
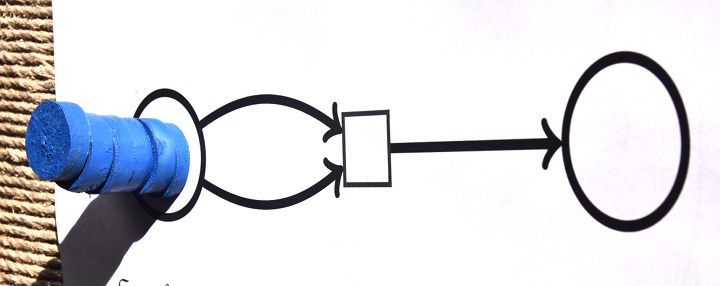
Ensuite on déclenche la transition :

Il reste 4 jetons à gauche et il y a un jeton à droite. Comme 4 est plus grand que 2, on peut encore déclencher la transition :

Et les 2 jetons restant à gauche permettent de déclencher une dernière fois la transition :
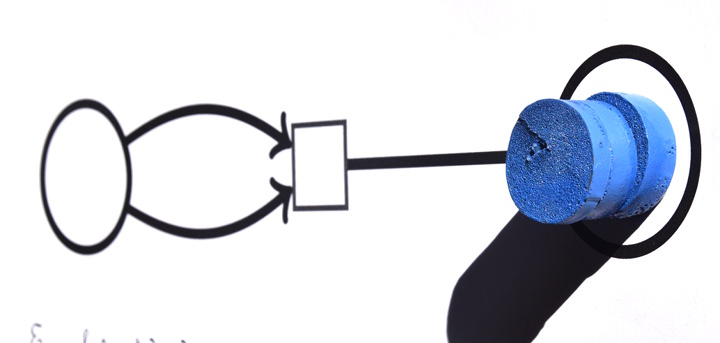
La transition ne peut plus être déclenchée parce qu’il n’y a plus de jeton en amont d’icelle (il faut au moins deux jetons) donc le calcul est terminé, et effectivement 3 est bien la moitié de 6.
Il s’agit d’une division euclidienne (avec reste éventuel). Par exemple comme il est interdit de couper les jetons en 2, si on divise 5 par 2 on aura successivement (5,0) :
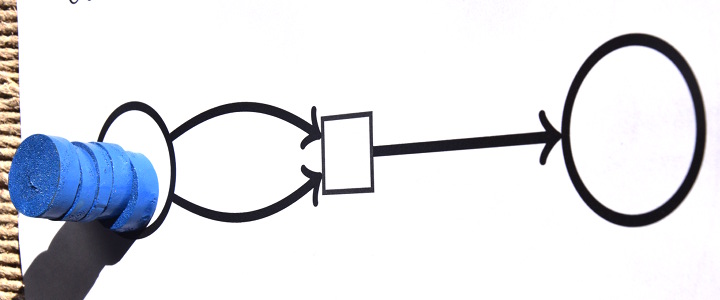
puis (3,1) :
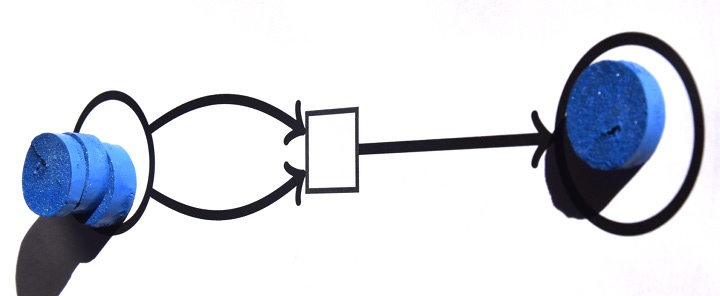
puis (1,2) :

et le calcul s’arrête là car pour déclencher la transition, il faut au minimum 2 jetons en amont, et il n’en reste plus qu’un. On lit à droite le quotient 2 et à gauche le reste 1.
Le vecteur d’incidence de ce réseau est
| -2 |
| 1 |
et x+2y est invariant (ce qui prouve qu’il s’agit bien d’une division euclidienne par 2).
En enchaînant des diviseurs par 2, on a un automate qui convertit en binaire :
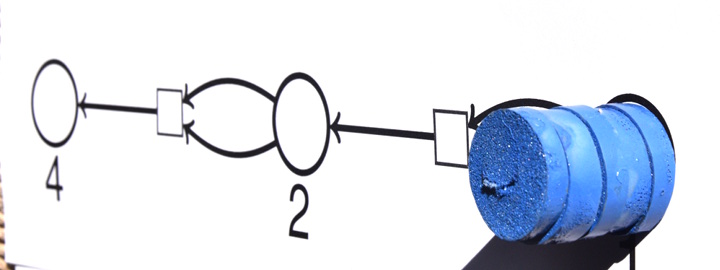
Pour obtenir l’écriture binaire de 5, on a placé 5 jetons dans la place de droite (valeur 1) et effectivement 5×1=5. Ensuite on peut déclencher la transition de droite ce qui transforme 5×1 en 3×1+1×2 :

puis on déclenche à nouveau cette transition pour obtenir une nouvelle écriture de 5 (1×1+2×2) :

Comme il ne reste plus qu’un jeton dans la place de droite (valeur 1) on ne peut plus déclencher la transition de droite. Mais la transition de gauche est maintenant active puisqu’il y a 2 jetons en amont de celle-ci. La déclencher revient à remplacer 2×2 par 1×4 :

Le calcul est maintenant terminé, et comme chaque place ne contient que 0 ou 1 jeton, l’écriture de 5 qu’on a obtenue est binaire (4+1 ou 101) :

La matrice d’incidence de ce réseau de Petri est
| -2 | 0 |
| 1 | -2 |
| 0 | 1 |
Et x+2×y+4×z est invariant, ce qui prouve qu’on obtient bien l’écriture binaire. Par exemple pour l’écriture de 5
état x+2×y+4×z
------------------------
(5,0,0) 5+2×0+4×0=5 état initial
(3,1,0) 3+2×1+4×0=5
(1,2,0) 1+2×2+4×0=5
(1,0,1) 1+2×0+4×1=5 état finalVoici la version awalé de ce réseau de Petri :
C’est le genre de calcul qui se font dans les marges de l’abaque binaire de Neper-Lucas, et l’abaque de Neper, utilisé pour la multiplication, est lui-même un réseau de Petri :
Toutefois ce réseau est peu pratique, car les places sont petites et nécessitent des jetons petits, donc difficiles à se procurer et à manipuler.
Minimum
Qu’est-ce qu’il se passe lorsque dans le réseau de Petri duplicateur, on inverse le sens des flèches ?
Par exemple si les deux places d’entrée (à gauche) contiennent respectivement x=5 jetons et y=2 jetons (et z=0 car on est dans l’état initial) :
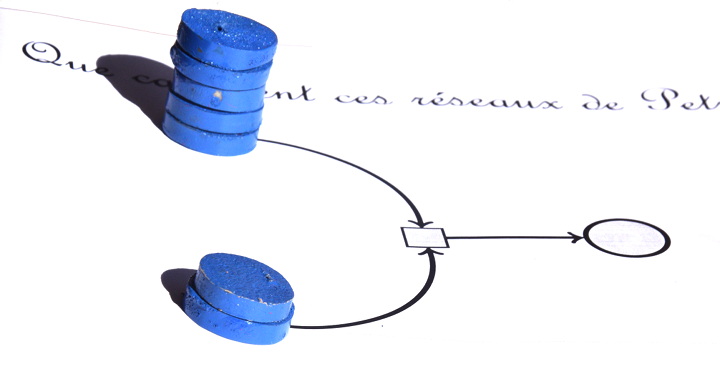
Les états successifs du VAS sont
(5,2,0) (état initial)
(4,1,1)
(3,0,2) (état final)
Le vecteur d’incidence est donc
| -1 |
| -1 |
| 1 |
Les deux quantités invariantes sont x+z et y+z (dans l’exemple ci-dessus, x+z=5 et y+z=2, on peut en déduire que x-y=3 et le réseau de Petri a effectué une soustraction : 5-2).
Ce réseau de Petri est plus mystérieux :

Avec au départ, x=2 et y=5 (et z=0 puisqu’on est dans l’état initial) on peut déclencher une première fois la transition :

puis une seconde et dernière fois :

En effet d’une part il n’y a plus de jeton dans x et la transition ne peut se déclencher que s’il y a suffisamment de jetons en amont, d’autre part il n’y a plus assez de jeton dans y (la transition consomme deux jetons de y).
Le vecteur d’incidence de ce réseau de Petri est
| -1 |
| -2 |
| 1 |
et le réseau possède deux invariants : x+z=2 et y+2×z=5. On en déduit que y-2x est également invariant : le réseau de Petri a soustrait le double de x à y (le résultat est dans y). Que se passe-t-il si x est plus grand que la moitié de y ?

Ici on a x=3 et y=4 (dont la moitié est effectivement plus petite que x). Après le premier déclenchement de la transition, on a le vecteur (x,y,z)=(2,2,1) :

Puis on réactive la transition une dernière fois et on a (1,0,2) :
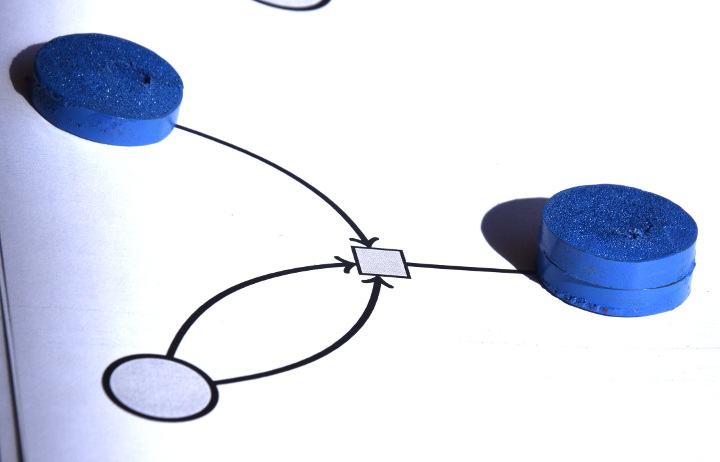
Le réseau de Petri a alors soustrait la moitié de y à x (résultat dans x).
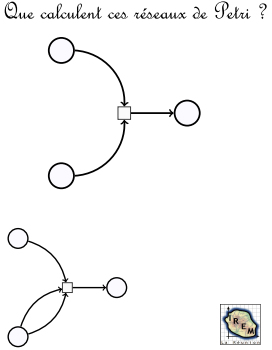
Il paraît peu naturel de dire que le résultat d’une opération est dans une place ou dans l’autre selon le cas, et la seule place qui ressemble à un résultat de calcul, est z. La question reste alors : que calcule ce réseau de Petri ?
En fait la réponse est relativement simple : le réseau de Petri calcule (dans z) le plus petit des nombres suivants :
- x
- la moitié entière de y (quotient euclidien de y par 2)
Binaire
Ce réseau de Petri est binaire, c’est-à-dire que chaque place contient au maximum un jeton :
Voici sa matrice d’incidence :
| 1 | 0 | -1 | 0 |
| -1 | 0 | 1 | 0 |
| 1 | -1 | -1 | 1 |
| 0 | 1 | 0 | -1 |
| 0 | -1 | 0 | 1 |
| 0 | 0 | 0 | 0 |
et les quantités invariantes sont (en appelant x, y, z, t, u les nombres de jetons dans les places alignées, de gauche à droite, et v le nombre de jetons en bas) :
- x+y
- y+z+t
- t+u
- v
En fait il n’y a qu’un jeton dans v, et ce jeton y reste toujours.
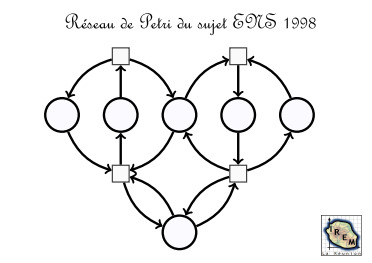
Ce réseau de Petri est issu de ce sujet de concours aux grandes écoles :
Dans le sujet de concours, le marquage initial du réseau de Petri est celui-ci :

On nomme a,b,c,d les 4 transitions, avec la convention suivante :
- a est en haut à gauche (nord-ouest)
- b est en haut à droite (nord-est)
- c est en bas à gauche (sud-ouest)
- d est en bas à droite (sud-est)
Alors dans l’état initial S0 on voit que les transitions b (nord-est) et c (sud-ouest) sont coloriées en vert : cela signifie qu’elles peuvent être déclenchées, mais ni a ni d ne peut être déclenché.
Si, dans l’état S0, on déclenche c, on passe à ce nouvel état S1 :
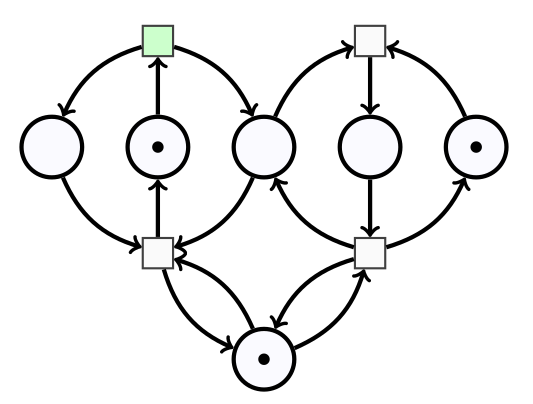
dans lequel seule la transition a peut être déclenchée. Si on la déclenche le réseau retourne dans l’état S0.
Si, par contre, dans l’état S0, on déclenche la transition b, le réseau passe dans cet état S2 :
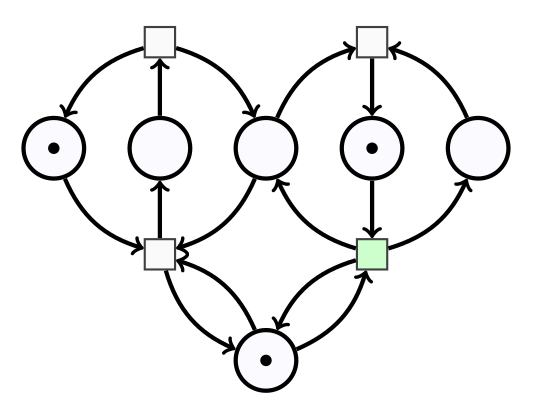
dans lequel seule la transition d peut être déclenchée. En la déclenchant, le réseau revient à l’état S0.
Toute cette histoire se résume dans ce graphe (en fait c’est un automate) :
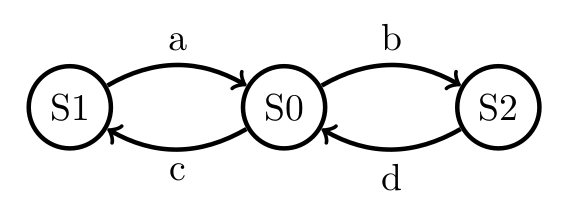
On appelle graphe de couverture le graphe des états accessibles à partir de l’état intial du réseau de Petri. Le graphe de couverture dépend du marquage initial. Dans le réseau de Petri ci-dessus, il y a d’autres états possibles (d’autres marquages) mais aucun d’entre eux n’est accessible à partir de l’état S0.
Un autre sujet de concours a porté sur les réseaux de Petri : agrégation de mathématiques 1997 :
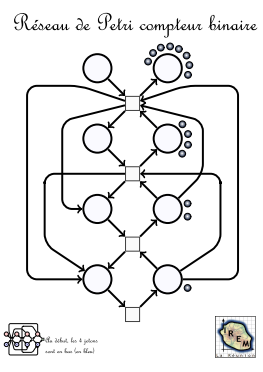
Un autre exemple de réseau de Petri binaire est ce compteur binaire :
Par exemple à ce stade du comptage, les jetons de l’avant (de droite à gauche) représentent le nombre 0101 soit 5 en binaire.
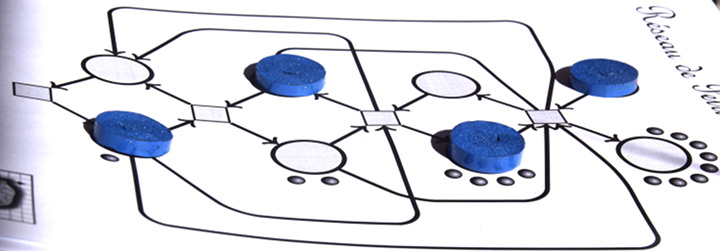
On peut imaginer que les billes de devant sont des lampes sensibles à la proximité d’un jeton, et s’allument (uniquement s’il y a un jeton pas loin). Alors on voit que 5 lampes sont allumées (en rouge) :
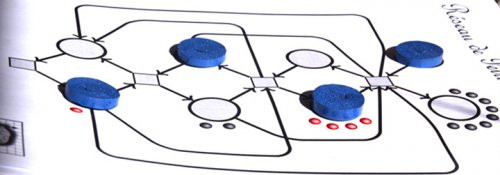
ce qui signifie que la représentation binaire 0101 est bien celle de 4+1=5.
Voici la matrice d’incidence de ce réseau de Petri (de - ou de haut en bas - pour les places du haut, de gauche à droite - ou de bas en haut - pour celles du bas et de droite à gauche pour les transitions) :
| 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 |
Il y a 4 invariants : les nombres totaux de jetons dans deux places à la verticale. Par exemple, tout à droite, ou bien il y a un jeton en bas, ou bien il y en a un en haut, mais pas les deux. Donc le nombre total de jetons est invariant et égal à 4.
Voici un autre compteur, unaire et non borné :

Il ressemble à un diviseur par 2, mais une des flèches a été inversée. Ce qui fait qu’à chaque déclenchement de son unique transition, un seul jeton est absorbé mais deux jetons sont injectés, l’un dans la place d’arrivée (à droite) et l’autre revient au départ :
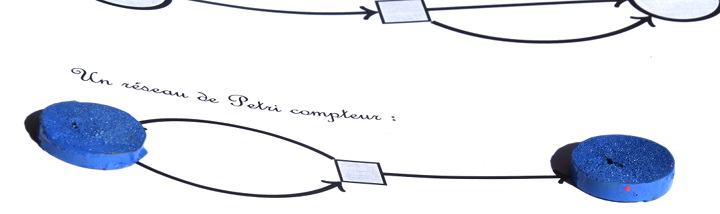
ce qui permet de redéclencher la transition :
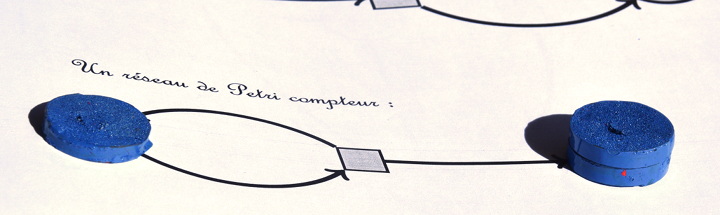
et encore une fois :
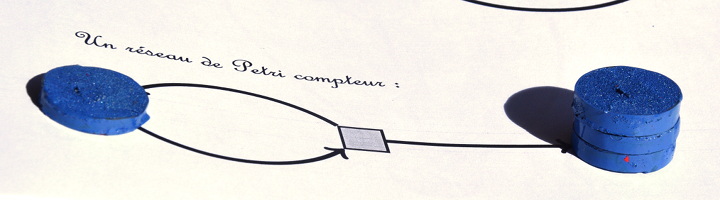
et encore :

et encore :
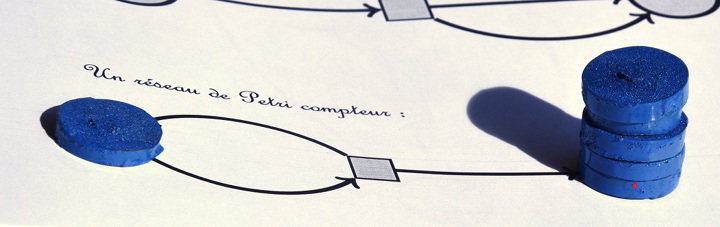
et ainsi de suite : ce réseau de Petri n’est pas borné. Il compte le nombre de fois que la transition a été déclenchée. D’ailleurs la transition consomme le jeton de gauche mais juste après, le réinjecte à gauche. Le vecteur d’incidence de cette transition est donc
| 0 |
| 1 |
et il n’y a pas d’invariant.

Lorsqu’un réseau de Petri est binaire, on peut remplacer les jetons par des pions plus en hauteur, et lorsqu’une partie d’un réseau de Petri est binaire, on utiise de préférence un pion pour montrer la différence par rapport aux jetons empilables. C’est ce qu’on fera pour le réseau de Petri multiplicateur, dont l’un des jetons joue un rôle spécial.
Nim
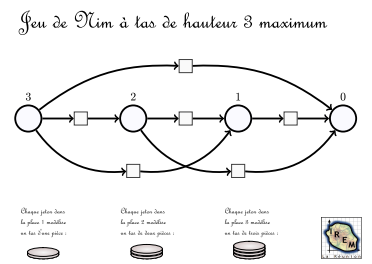
Ce réseau de Petri, tout comme le compteur binaire, modélise quelque chose : un jeu de Nim à tas de taille 3 maximum :
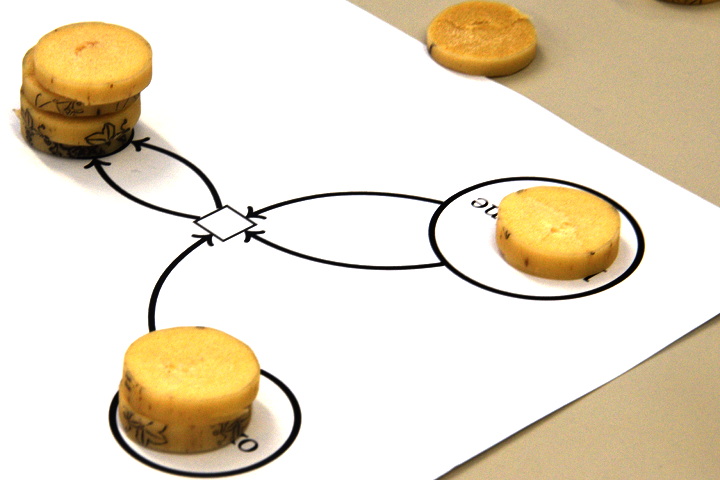
Par exemple si on joue à Nim avec deux tas, l’un de 3 pièces (en rouge), l’autre de 2 pièces (en bleu) :

alors le coup consistant à retirer une pièce du tas de 3, revient à bouger le jeton (rouge) qui est dans la place « 3 pièces » et le mettre dans la place « 2 pièces » :

Remontrons cela avec les tas de pièces rouges, et en même temps leur modélisation sur le réseau de Petri (en bleu). Un tas de 3 pièces est modélisé par un jeton dans la place de gauche (laquelle représente les tas de 3 pièces, ici il n’y en a qu’un), et un tas de 2 pièces est modélisé par un autre jeton, dans la seconde place en partant de la gauche (elle modélise les tas de 2 pièces) :

Alors le retrait d’une pièce, du tas de 3, revient à transformer ce tas en un tas de 2, ce qui se modélise par une transition : le jeton représentant un tas de 3 bouge pour la place des tas de 2 :
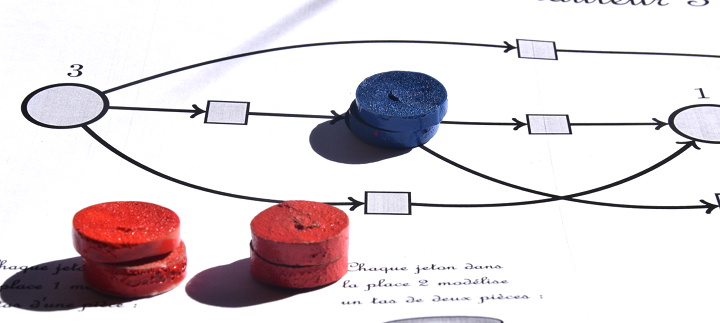
La matrice d’incidence de ce réseau est
| -1 | 0 | 0 | -1 | 0 | -1 |
| 1 | -1 | 0 | 0 | -1 | 0 |
| 0 | 1 | -1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 |
et la quantité totale de jetons x+y+z+t est invariante.
En fait chaque transition ayant exactement une entrée et une sortie, ce réseau de Petri est un automate.
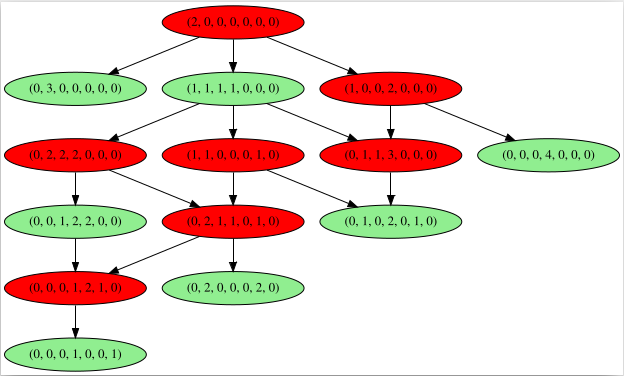
Le graphe de couverture donne alors une stratégie gagnante à ce jeu de Nim :
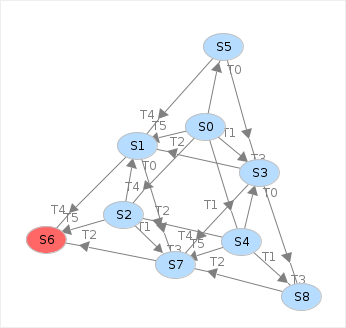
Pour décrire les états, il suffit de préciser, pour chaque jeton, s’il est en x, en y, en z ou en t :
S0: (x,y) état initial
S1: (y,t)
S2: (x,t)
S3: (y,z)
S4: (x,z)
S5: (y,y)
S6: (t,t) état final (interblocage)
S7: (z,t)
S8: (z,z)Chaque arc indique le déclenchement d’une transition qui fait aller d’un état à un autre. Par exemple la présence d’un arc entre S0 et S5 signifie qu’il est possible d’aller de l’état S0 = (1,1,0,0) à l’état S5=(0,2,0,0) en déclenchant la transition T0 (celle de gauche). Pour obtenir la stratégie gagnante à ce jeu, on colorie les sommets du graphe de couverture, par exemple avec Nirina974 :

La stratégie gagnante consistant à aller vers un sommet vert, la transition vers S5 était donc la meilleure possible : on se retrouve avec 2 tas de 2 pièces et à partir de là, il suffit d’imiter les coups de l’adversaire pour gagner à coup sûr.
Voici le graphe de couverture, au format Nirina974 :
Multiplication
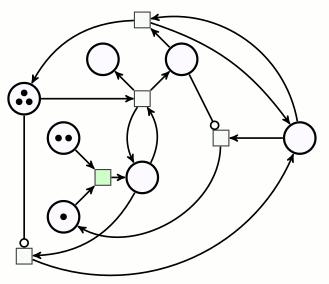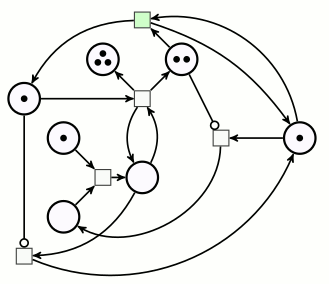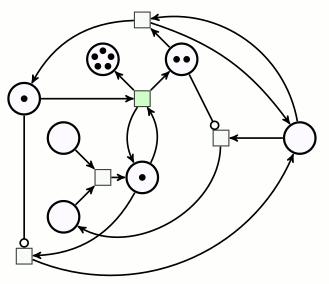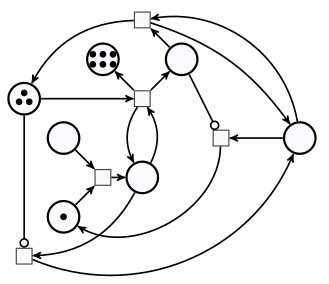
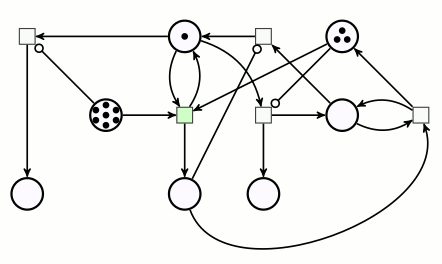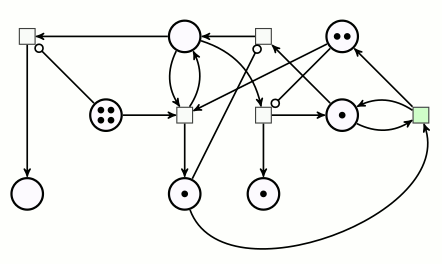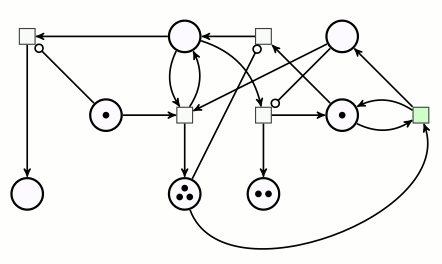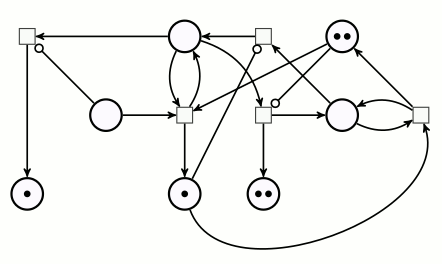
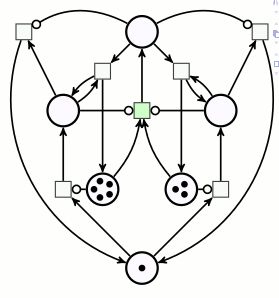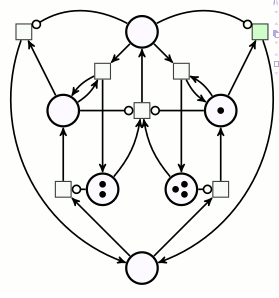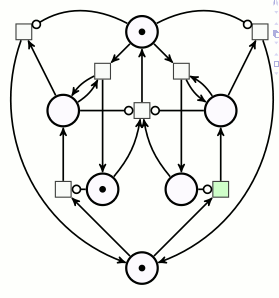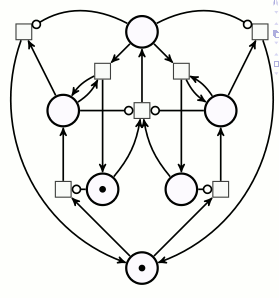
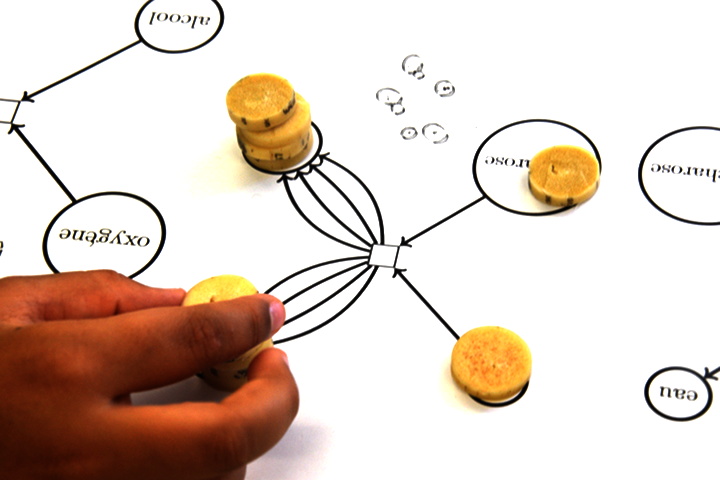
Ce réseau de Petri comprend deux arcs inhibiteurs :
On reconnaît un arc inhibiteur au fait que la pointe de flèche y est remplacée par un petit cercle.
Les transitions correspondantes ne peuvent être déclenchées que s’il y a suffisamment de jetons en amont, sauf sur l’arc inhibiteur, où, au contraire, il ne faut pas qu’il y ait de jeton.
Le réseau est doté de deux catégories de places :
- les deux places de gauche et celle qui est tout en bas constituent un sous-réseau de Petri binaire : aucune ne contiendra plus d’un jeton à la fois (on représentera ce jeton solitaire par un pion d’aspect différent des autres jetons).
- Les quatre autres places sont comme celles des réseaux de Petri du début, les nombres de jetons posés dessus représentent des variables entières.
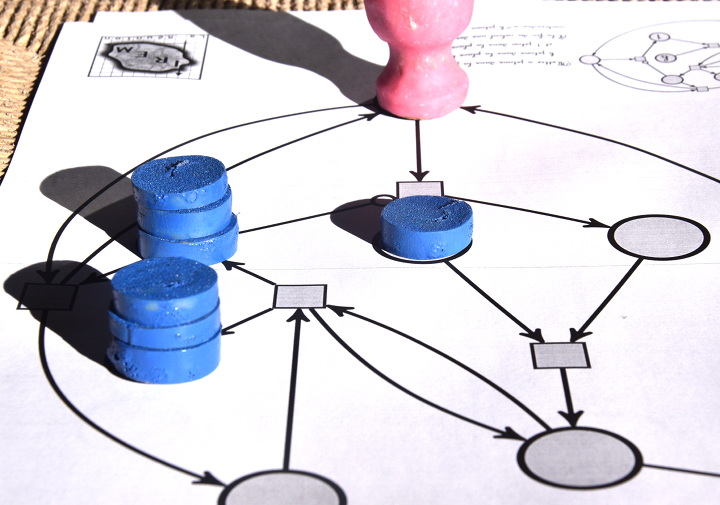
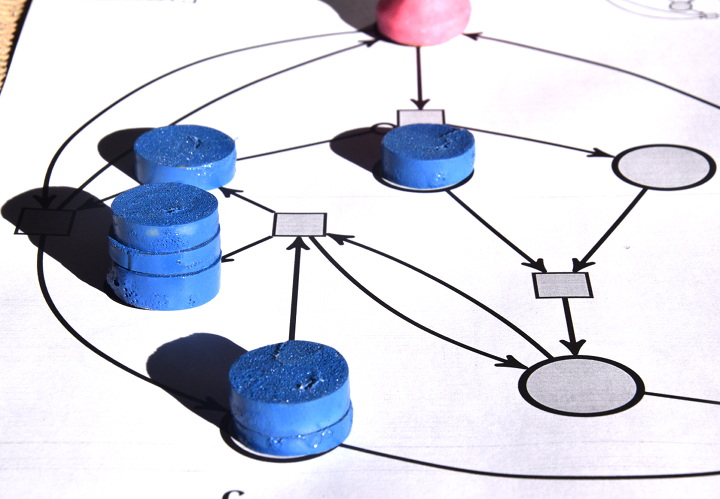
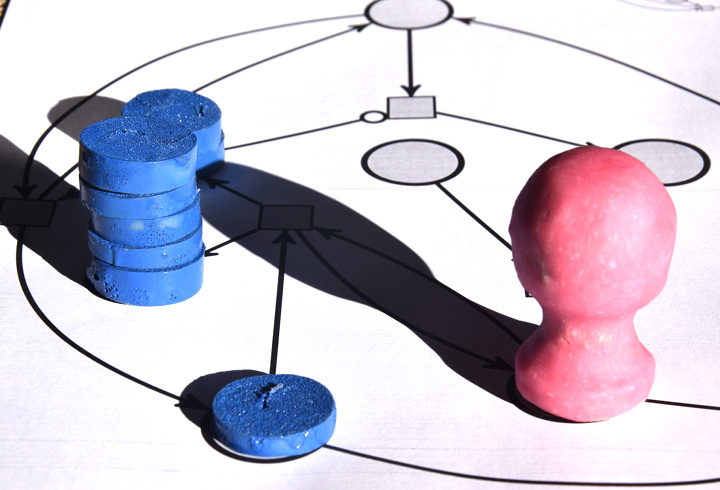
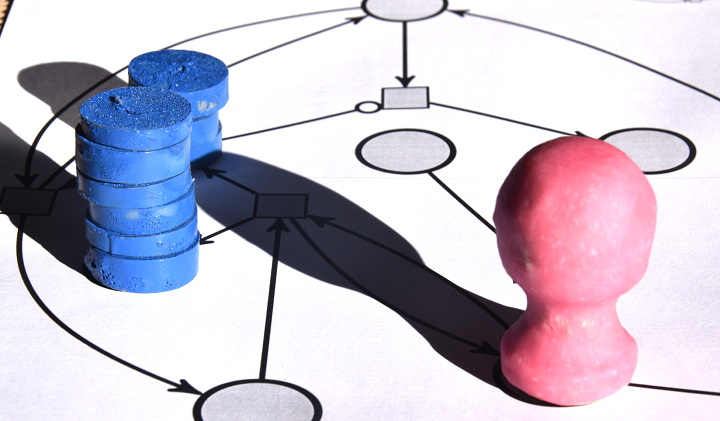
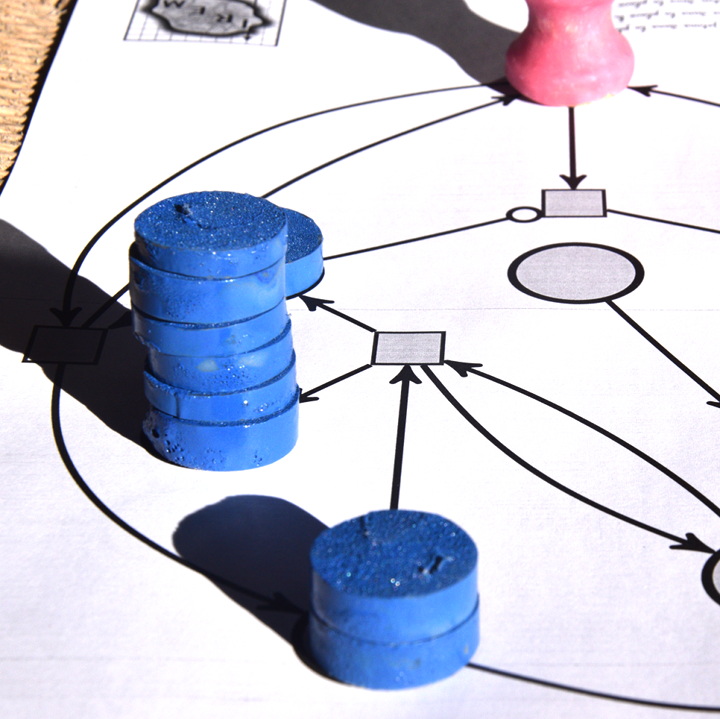
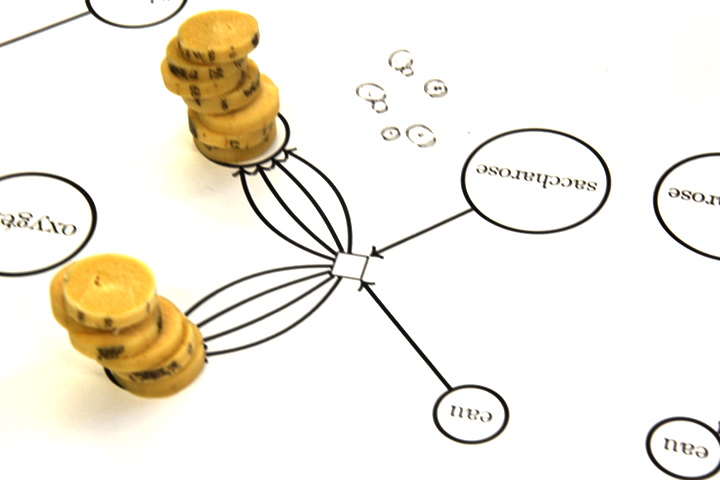
Pour effectuer la multiplication de 3 par 2, on dispose 3 jetons sur la place du multiplicande, et 2 jetons sur la place du multiplicateur. Le démarrage du calcul se fait en ajoutant un pion sur une place signifiant « on est au début d’une décrémentation-addition » :
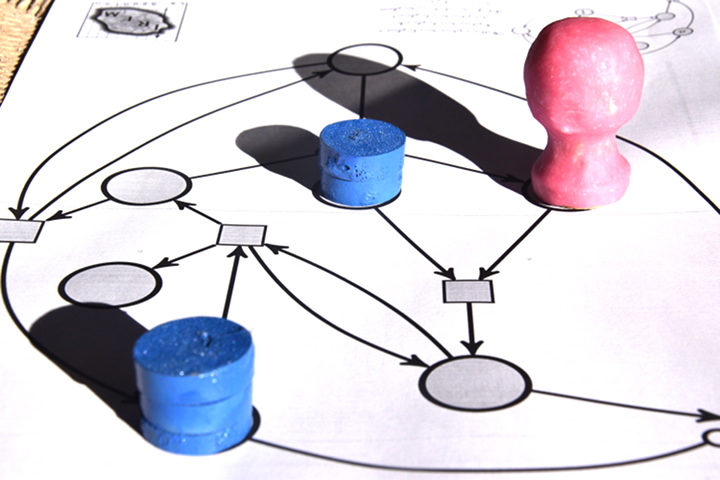
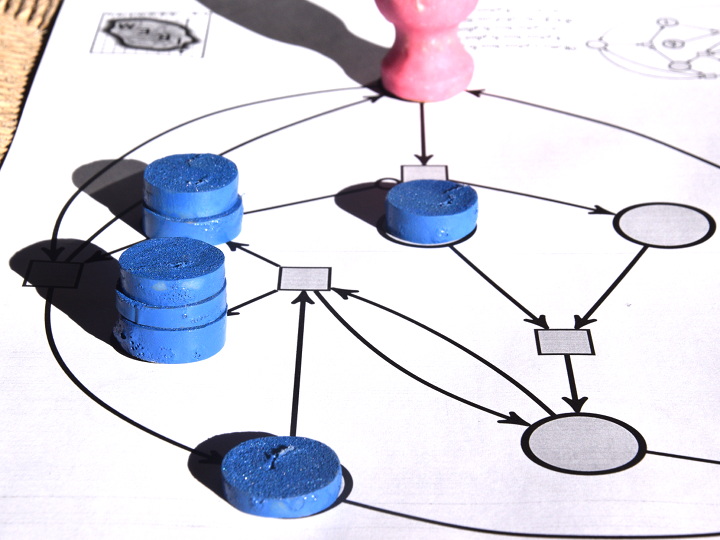
La suite sera assez longue donc articulée par phases : chaque phase correspond à une position du pion rose sur le réseau de Petri.
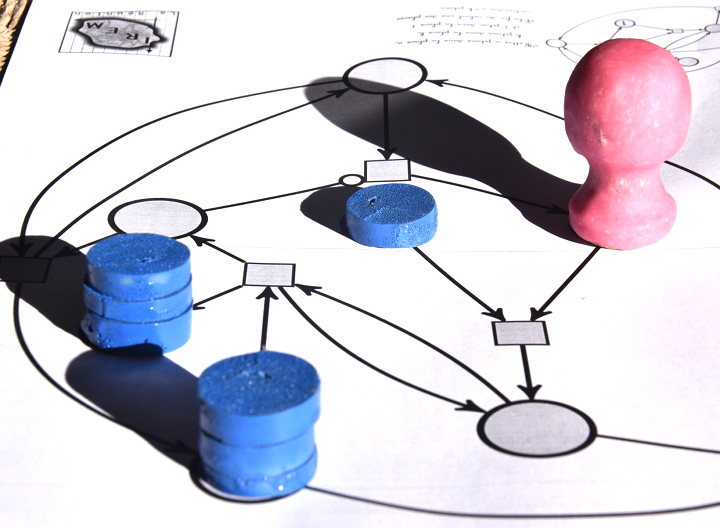
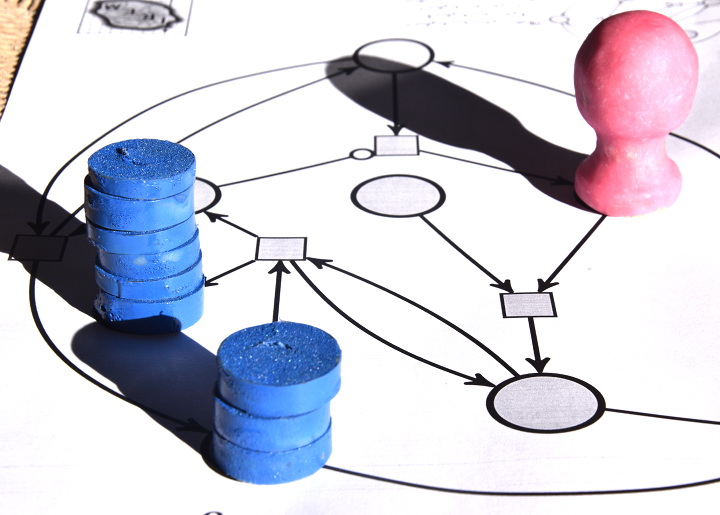
Plus aucune transition ne peut être déclenchée parce qu’aucune d’entre elles ne dispose de suffisamment de jetons en amont, donc le calcul est terminé. Comme il y a 6 jetons sur la place d’arrivée, on voit bien que 3×2=6. Concrètement, à moins de disposer de jetons très plats (pièces de monnaie ?) on ne peut pas effectuer de grandes multiplications sur ce réseau de Petri. Par exemple la multiplication 4×3, outre qu’elle dure plus longtemps, aboutit à un tas de 12 jetons, qui est instable de par sa hauteur.
On constate sur les arrêts sur image ci-dessus, que chaque fois que le pion est revenu au départ,
- le multiplicateur est diminué d’une unité,
- le produit est augmenté de 3 unités (plus généralement, du multiplicande).

De fait, ce réseau de Petri effectue une addition itérée avec mémorisation d’un facteur, ce que Conway appelait multiplication non destructrice. On peut étendre ce réseau pour effectuer d’autres opérations, utilisant la multiplication itérée.
Ce réseau de Petri possède deux invariants :
- la quantité totale de jetons sur les trois places où évolue le pion, est égale à 1 : cela signifie que seul le pion évolue sur ces trois places,
- la quantité totale des jetons sur les places du multiplicande et du produit partiel est constante (égale à 3 par exemple). Cela implique que le multiplicande est toujours à sa place à la fin du calcul.
Division
Ce réseau de Petri calcule une division euclidienne (le reste et le quotient sont dans les deux places du bas quand le pion est dans la place en bas à gauche) ; ci-dessous la division de 7 par 3 donne le reste 1 et le quotient 2 :
Un clic sur l’image animée ci-dessus permet de télécharger le réseau de Petri au format pdf.
pgcd
De façon similaire, ce réseau de Petri à 4 arcs inhibiteurs implémente l’algorithme d’Euclide :
En effet il représente sous une forme graphique le « on soustrait toujours alternativement le plus petit du plus grand » prôné par Euclide dans le livre VII de ses
éléments :


Il ne s’agit finalement que d’une version itérée du réseau de Petri de l’onglet minimum.
Jeu à 2 joueurs
Ce jeu avait déjà été proposé lors d’animations (fête de la science, semaines des maths) :
Mais cela avait révélé qu’il est complexe et même des lycéens l’avaient trouvé fatigant.
En numérotant les places de haut en bas et de droite à gauche (idem pour les transitions), la matrice d’incidence de ce réseau est
| -1 | -1 | -2 | 0 | 0 | 0 |
| 2 | 1 | 0 | -1 | 0 | 0 |
| 0 | 1 | 0 | -1 | -1 | 0 |
| 0 | 1 | 3 | 0 | -2 | 0 |
| 0 | 0 | 0 | 1 | 0 | -1 |
| 0 | 0 | 0 | 0 | 2 | -2 |
| 0 | 0 | 0 | 0 | 0 | 1 |
- Avec un seul jeton au départ, le graphe de couverture comporte 4 sommets dont 2 aboutissent à la fin du jeu. La stratégie gagnante consiste à jouer la transition de gauche qui bloque le réseau de Petri (et à qui perd gagne, jouer la transition du milieu oblige l’adversaire à jouer la dernière transition, bloquante) :
Le vecteur (0,0,0,2,0,0,0) été colorié en vert parce que le joueur A veut y aller : aucune transition n’est active avec ce vecteur et le jeu est terminé. Si A avait joué la transition du milieu, le vecteur (0,1,1,1,0,0,0) aurait permis le déclenchement de la transition en bas à gauche, aboutissant à (0,1,0,0,0,1,0) et au blocage du réseau de Petri (sur la victoire de B). A n’a donc pas intérêt à jouer la transition du milieu et le vecteur (0,1,1,1,0,0,0) a donc été colorié en rouge.
- Avec 2 jetons au départ le graphe comporte 14 sommets dont 5 sont des positions de fin de jeu. En particulier celui qui joue en premier dispose d’une stratégie gagnante rapide en jouant la transition de droite (dessinée à gauche ci-dessous) qui bloque immédiatement le réseau de Petri.
La coloration du graphe a été faite avec la technique évoquée dans cet article et comme pour le cas à 1 jeton au départ, la stratégie gagnante consiste à toujours aller vers un vecteur vert. Comme le vecteur initial est rouge, cela signifie que le joueur qui joue en premier dispose d’une stratégie gagnante. Est-ce que c’est toujours le joueur qui joue en premier, qui gagne ?
- Avec 3 jetons au départ le graphe comporte 35 sommets dont 9 sont des fins de jeu :
Ici le sommet du haut est vert, ce qui signifie que quoi que joue le premier joueur, le second disposera d’une stratégie gagnante. C’est donc le second joueur qui gagne.
- Avec 4 jetons au départ (cas évoqié dans le livre page 141) le graphe comporte 83 sommets dont 16 sont des positions finales (réseau de Petri bloqué). Le vecteur (4,0,0,0,0,0,0) est rouge ce qui signifie que là, le joueur qui joue en premier gagne le jeu (s’il joue au mieux) :
- Avec 5 jetons au départ il ne reste plus que 172 sommets. Là c’est le joueur qui joue en deuxième, qui dispose d’une stratégie gagnante :
- Avec 6 jetons dans la place de départ avant de jouer, le graphe de couverture comporte 329 sommets. La stratégie gagnante est pour le joueur qui joue en premier :
- Avec 7 jetons au départ, la stratégie gagnante est pour le joueur qui joue en ... euh je sais pas, les calculs sont vraiment très longs. Le script Python pour dessiner le graphe est celui-ci :
from graphviz import Digraph
def sommevec(u,v):
return tuple([u[k]+v[k] for k in range(len(u))])
def positif(v):
return all(v[k]>=0 for k in range(len(v)))
transitions = [(-2,3,0,0,0,0,0),(-1,1,1,1,0,0,0),(-1,0,0,2,0,0,0),(0,-2,-1,0,2,0,0),(0,0,-1,-1,0,1,0),(0,0,0,0,-2,-1,1)]
v = (7,0,0,0,0,0,0)
dico = {}
vus = []
explorer = [v]
while len(explorer):
s = explorer.pop(0)
if s not in vus: vus.append(s)
for t in transitions:
u = sommevec(s,t)
if positif(u):
if s in dico and u not in dico[s]:
dico[s].append(u)
else:
dico[s] = [u]
if u not in vus:
explorer.append(u)
verts = []
rouges = []
for v in dico.values():
for s in v:
if s not in dico.keys() and s not in verts:
verts.append(s)
for layer in range(8):
for s in dico:
if any(t in verts for t in dico[s]):
if s not in rouges:
rouges.append(s)
for s in dico:
if all(t in rouges for t in dico[s]):
if s not in verts:
verts.append(s)
print(len(verts),len(rouges),len(dico))
g = Digraph(format='svg',strict=True)
for s in verts:
g.node(str(s),style='filled',fillcolor='lightgreen')
for s in rouges:
g.node(str(s),style='filled',fillcolor='red')
for s in dico:
for t in dico[s]:
g.edge(str(s),str(t))
g.render('petria7c')Jeu en ligne
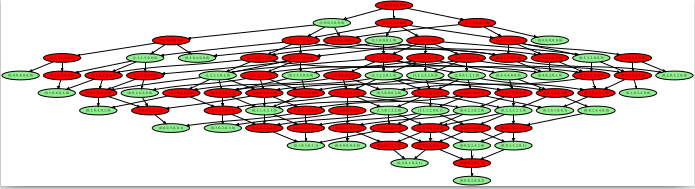
Dans le livre (page 149) est présenté un autre jeu sur réseau de Petri, auquel on peut jouer en ligne. Le graphe de ce jeu est surprenamment complexe :
Le vecteur de départ étant rouge, la stratégie gagnante est pour le joueur qui joue en premier. À partir de la position de départ
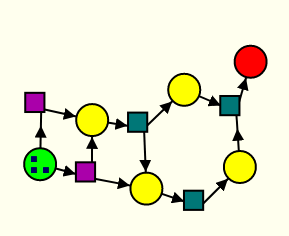
il a intérêt à jouer la transition du bas :
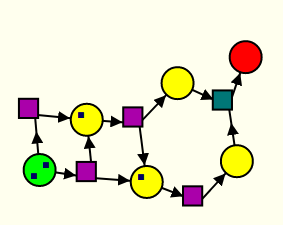
Sinon, en jouant la transition du haut :
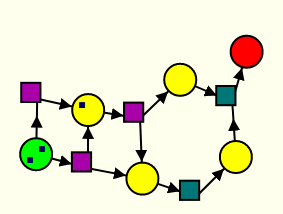
il aurait permis au second joueur d’aboutir à cette situation, gagnante pour le second joueur :

4e-3e
Les élèves du collège Michel Debré, malgré la brièveté de l’intervention, ont montré parfois des capacités impressionnantes en modélisation et en émission de conjecture.
L’occasion s’est présentée également d’évoquer la modélisation des échanges commerciaux internationaux par des réseaux de Petri : les jetons n’étant pas partageables entre les transitions, chaque place représente une ressource dont la quantité disponible est limitée, et chaque transition représente une entreprise ou un pays, qui, s’il prélève le jeton, en prive les autres transitions, ce qui est potentiellement source de conflits.
Doubleur
Avant de démarrer l’activité, on a peu d’idée de la quantité de jetons nécessaire à la fin :

Les élèves ont souvent besoin de manipuler pour comprendre qu’il y aura production de jetons.
Même en se contentant de seulement 4 jetons avant l’expérience, on en a tout de même 8 à l’arrivée :


Le réseau tripleur aussi pose des problèmes de compréhension : il y a écrit tripleur alors on met 3 jetons au départ :
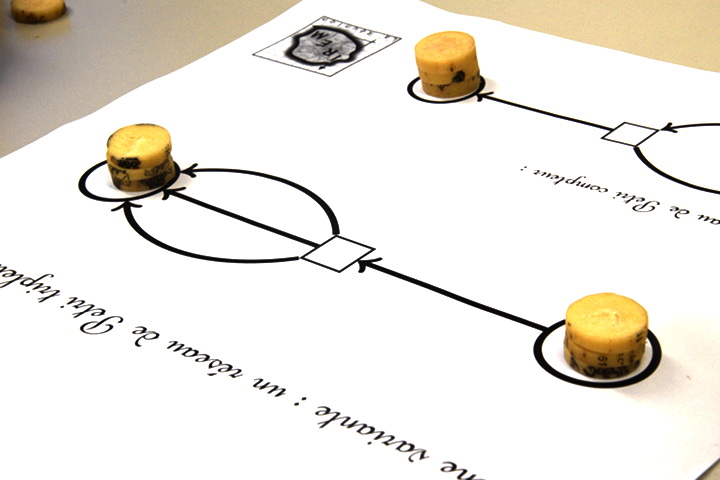
Clonage
Le réseau duplicateur met en œuvre une certaine virtuosité, à cause du fait que pour chaque jeton absorbé il y a 2 jetons injectés. On commence par prendre un jeton de la place de départ, puis le glisser vers la transition :

puis, comme il manque un jeton, on en prélève un dans la réserve, on le pose sur une des places d’arrivées

puis dans le même mouvement on pose l’ancien jeton dans l’autre place d’arrivée :

Par contre la verbalisation est difficile. Souvent on entend « ça a doublé le nombre de jetons » sans préciser l’équirépartition.
Addition
Le réseau additionneur permet une accélération dans la manipulation. Pour activer la transition de droite, on fait glisser un jeton depuis la place en amont de la transition vers la transition

puis comme la transition ne produit qu’un jeton, on continue à le déplacer vers la place d’arrivée.

On finit par comprendre que chaque transition est simplement traversée par un jeton.
L’additionneur est l’occasion d’introduire la notion de graphe de couvrement, avec des arcs entre les vecteurs qui peuvent être atteints les uns à partir des autres, par activation d’une des transitions.
Le graphe a la forme d’une grille, esquissée ici par une élève de 3e :

Chaque flèche vers la droite est la translation de vecteur (-1,0,1) et chaque flèche vers le bas est la translation de vecteur (0,-1,1). Ces deux translations donnent au graphe une allure de pavage.
Soustraction
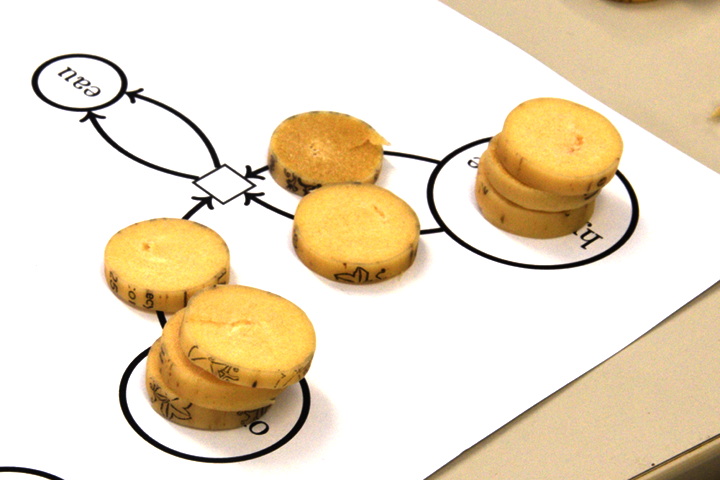
Au début on essaye avec autant de jetons dans chacune des places de départ :

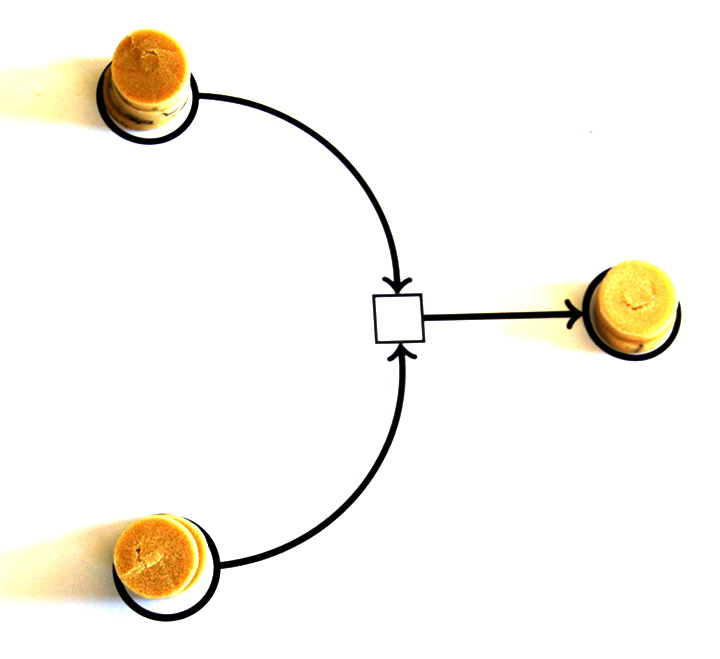
Par exemple s’il y avait deux jetons dans chacune des places on aboutit à ceci :

Dans ce cas particulier, on aboutit rapidement à une conjecture sur la moitié :

Pour émettre des conjectures, il est plus intéressant de généraliser. Par exemple avec 4 jetons et 2 jetons au début on aboutit à cette situation :

Et avec 4 jetons et 5 jetons au début on a

et à la fin, 4 jetons dans la place d’arrivée (et il reste un jeton dans une des places de départ).
Pour aider à l’émission de conjecture, et en même temps mettre en place un travail collaboratif, un tableau des valeurs possibles à l’arrivée a été commencé :
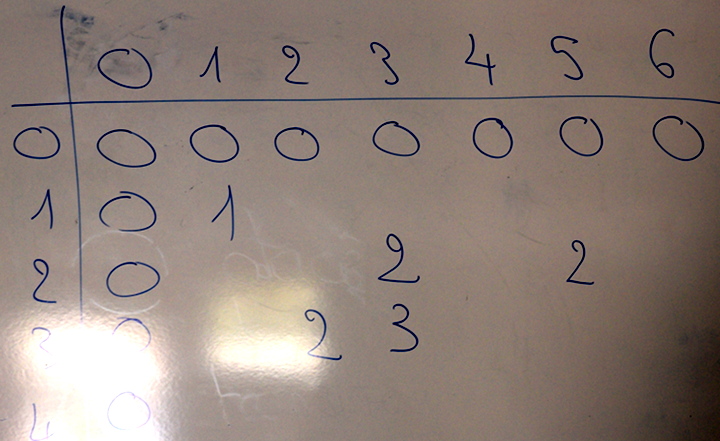
avec un degré d’avancement plus ou moins élevé selon les groupes :

Une aide à l’émission de conjecture (et à la preuve) est la notion d’invariant. Comme support de recherche, il a été demandé de tracer le graphe de couvrement (liste des vecteurs successifs) :
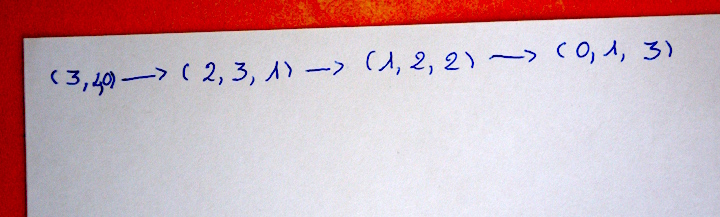
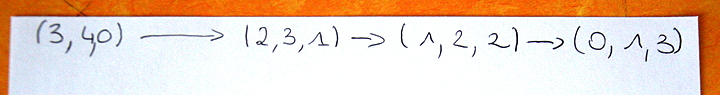
puis de chercher un invariant (de même valeur sur tous les vecteurs de la liste).
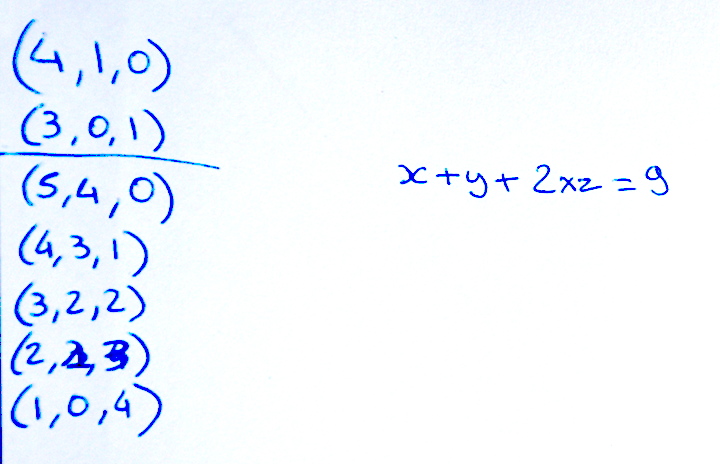
L’invariant x+y+2z n’a pas été trouvé spontanément, faute de temps. L’exercice est intéressant mais nécessite une longue préparation en amont (initiation aux réseaux de Petri).
Avec une situation de départ symétrique, une conjecture a également été émise sur le réseau mystérieux :

6e-5e
Au collège Antoine-Soubou, certains groupes ont pu rester un peu plus longtemps et cela a permis de mieux gérer les phases de l’expérimentation et d’obtenir des productions d’élèves particulièrement intéressantes.

marquage
L’exercice de marquage initial du réseau de Petri permet de se familiariser avec les jetons (masse, porosité, empilement), ceci avant même que l’on parle de transition.
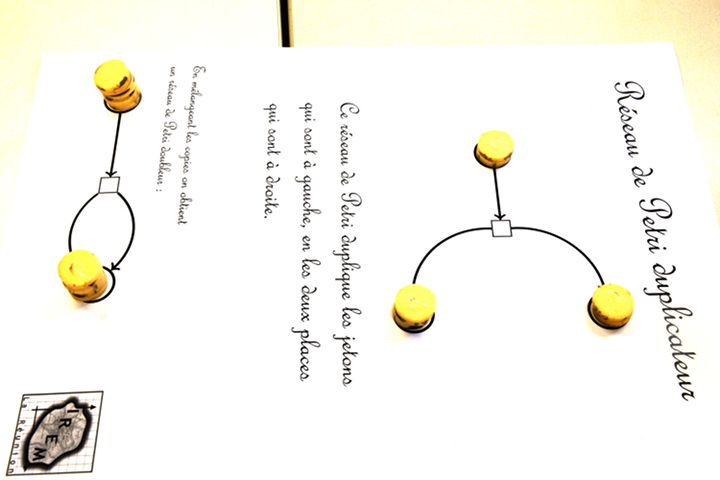
L’idée de mettre plus d’un jeton dans une place n’est pas spontanée :
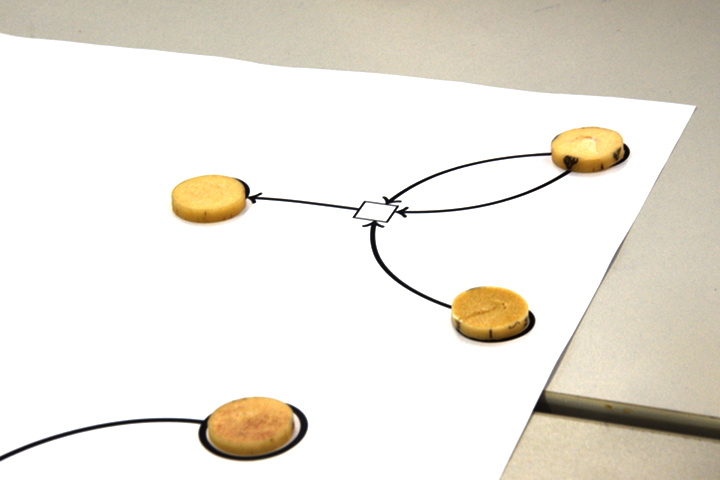
À ce stade les élèves manifestent un goût certain pour la symétrie :
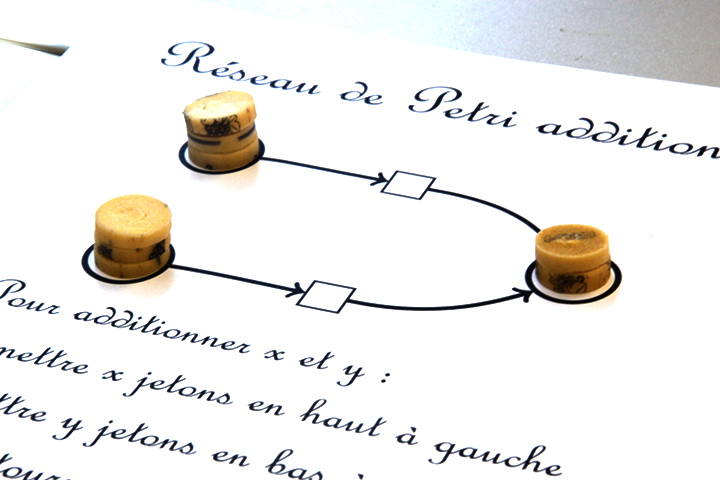
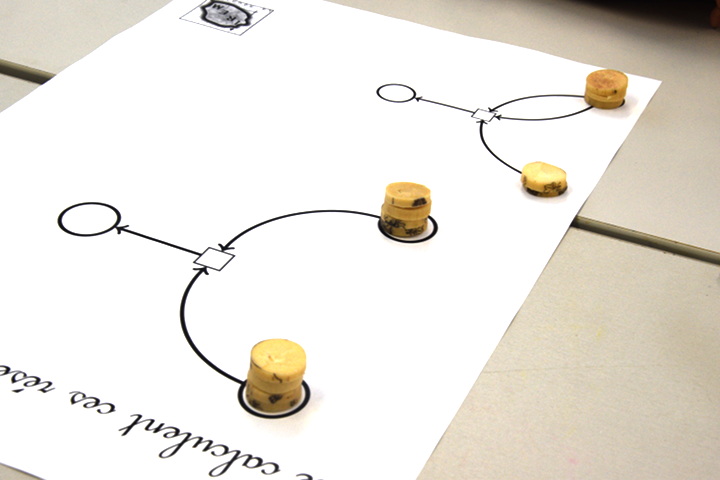




Cette étape permet d’avoir une connaissance tactile du réseau et ensuite il est expliqué
- que pour poser un calcul, on ne met pas de jeton dans les places dites finales (dont aucun arc n’émane)
- comment fonctionne une transition
double
Pour utiliser le réseau doubleur, à chaque fois qu’on a amené un jeton vers la transition, il est nécessaire de puiser dans la réserve car on a besoin d’un second jeton pour finir la transition
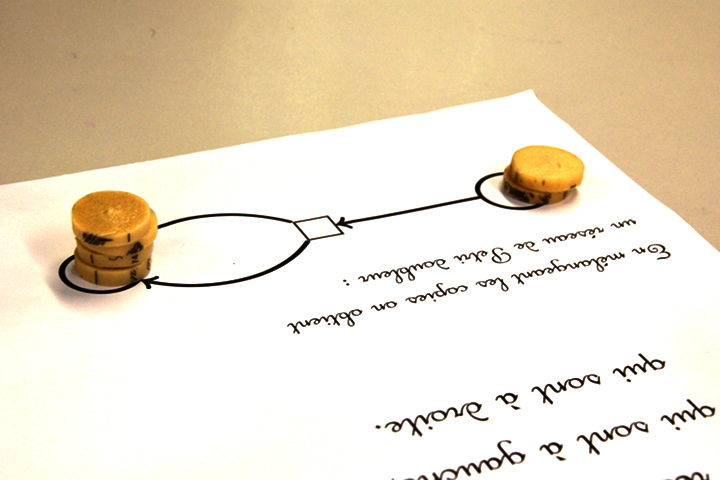
À la fin le nombre de jetons à l’arrivée est donc pair :

Ce qui permet de rapidement voir les erreurs :


(4 jetons dans la place à droite, qui devrait compter un multiple de 3)
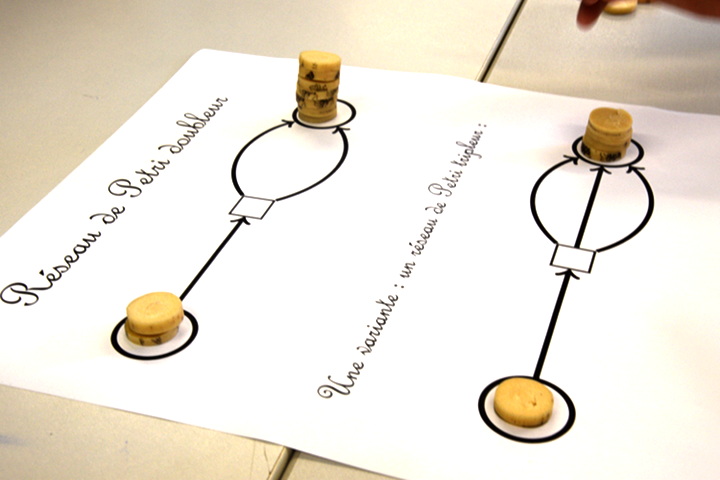
D’autres erreurs fréquentes sont les transitions commencées alors que la transition précédente n’est pas encore finie :


moitié
Dans le réseau de Petri diviseur par 2, il faut, à chaque activation de la transition, attraper 2 jetons

Avec de l’entraînement on peut les déplacer en même temps :

Parfois quand on a fini il reste un jeton dans la place de départ :

La construction d’un nuage de mots est un exercice intéressant car il révèle la nature du réseau sémantique des élèves : un groupe n’a pas pensé au mot « moitié » :
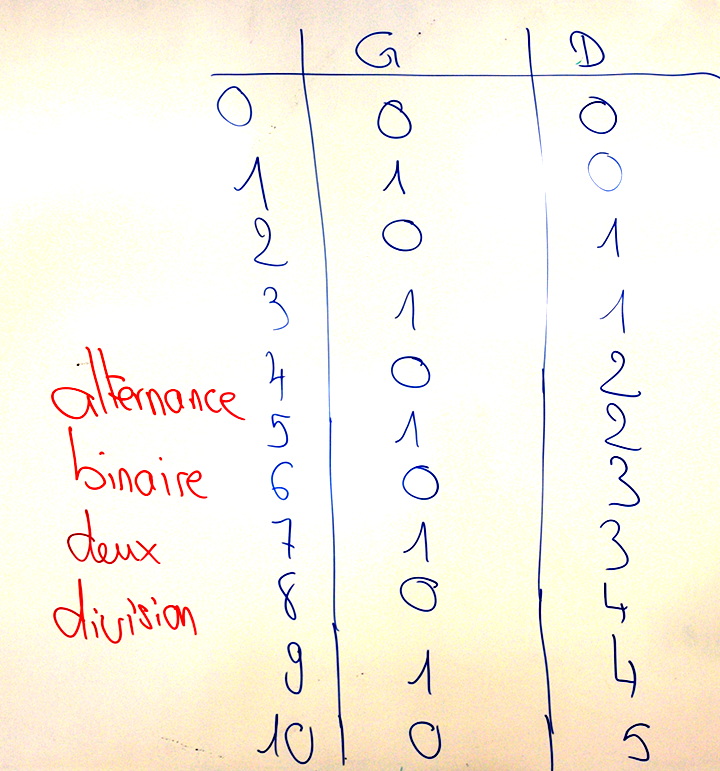
mais le mot « binaire » revient régulièrement :

Noter que pour le réseau soustraction-minimum, les mots ont été plus difficiles à trouver (verbalisation plus difficile) :

La question avait été « quels sont les mots que cette situation (le tableau de nombres) vous évoque ? ».
Dessin
Un groupe de 6e a offert le plus beau des cadeaux qu’on pouvait imaginer dans ce domaine : les élèves ont inventé leur propre réseau de Petri.
Duplicateur :

Triplicateur :
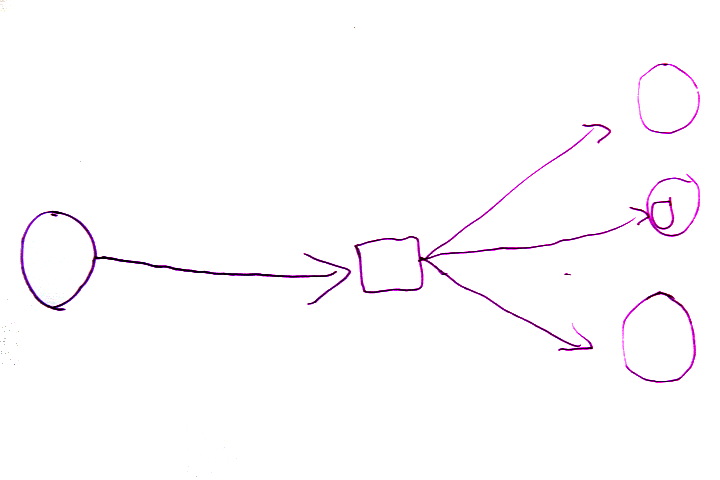

Triplicateur étendu :


Simulateur de big bang :
zéro transition :

une transition :
deux transitions :
trois transitions :

six transitions :

et ce chef-d’œuvre :
par la suite complété :
CM1-CM2
L’activité fait beaucoup travailler le comptage (des arcs, des jetons) et le calcul mental (combien de jetons aurait-on sur le réseau de Petri tripleur, si on avait posé 7 jetons au départ ?).
Le plus fascinant des réseaux de Petri en CM1 c’est celui qui ne s’arrête jamais (infini potentiel) :
tripleur
La verbalisation et le travail collaboratif se mettent vite à l’œuvre avec ce réseau. Un seul jeton est absorbé par la transition :

mais la transition produisant 3 jetons, il en manque deux, à prélever dans la réserve. C’est là qu’on s’y met à plusieurs :

Après il suffit d’empiler ces trois jetons sur la place d’arrivée :
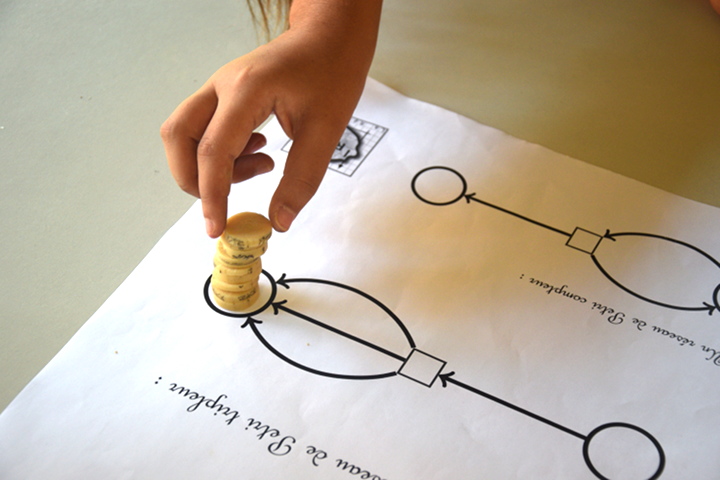
Addition
En CM1, le passage rapide du jeton au travers d’une transition simple, n’est pas automatique. Il y a un petit temps d’arrêt du jeton sur la transition :

Par contre le fait qu’on a le choix entre les deux transitions, apparaît vite. Ici il y a eu changement de transition par rapport à la photo précédente :

Lorsque les deux places de départ sont vides, le calcul est terminé, sur la somme des deux nombres de départ :
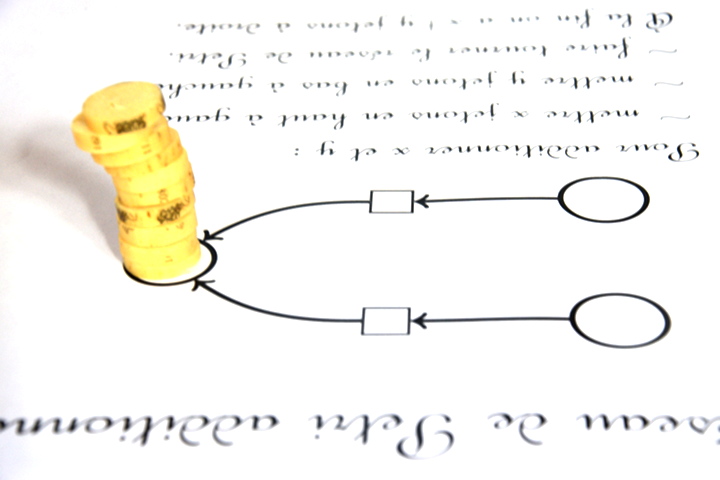
Soustraction
La transition a absorbé deux jetons (un de chaque place de départ) mais n’en produira qu’un. Il faut donc enlever (pour le remettre dans la réserve) un des deux jetons qui sont actuellement sur la transition :

Pour le réseau mystère c’est pareil : la transition absorbe 3 jetons et n’en produit qu’un. L’un des 3 jetons est déjà parti dans la réserve, un autre est en cours de retrait (ça va très vite) :

Ensuite le jeton restant va à l’arrivée :

Le goût pour la symétrie est présent dès le cours moyen :

Moitié
Le diviseur par 2 absorbe deux jetons à chaque transition :

Cela permet du collaboratif, les élèves bougeant les deux jetons en même temps (la transition a été comprise). Puis une élève enlève le jeton de trop (la division n’en produisant qu’un) tandis que l’autre amène le jeton restant à l’arrivée :

La division de 5 par 2 donne 2 comme quotient mais avec un reste de 1 (CM2) :
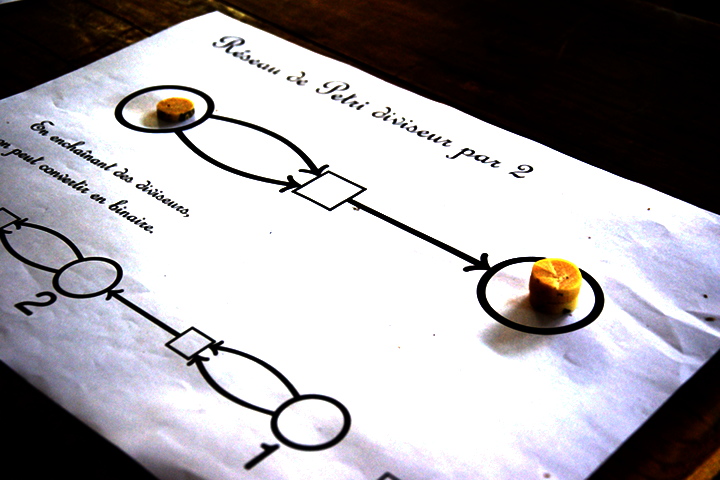
Cette division est douteuse : il devait y avoir beaucoup de jetons au départ :

Binaire
L’impatience de Maxime (CM1) a mené celui-ci à faire des conversions en binaire avec la chaîne de divisions par 2. Par exemple pour écrire 7 en binaire, il met 7 jetons au départ puis en amène 2 sur la transition :

Il retire l’un des deux d’une main et en même temps amène l’autre sur la place 2 :

Et il recommence (ça va très vite et pourtant il explique) : retrait de 2 jetons depuis la place 1 et prélèvement d’un des deux pour la réserve,

À ce stade il y a 3 jetons dans la place 1 et 2 jetons dans la place 2. Maxime et ses camarades ont compris qu’il y a un choix : continuer avec 2 des 3 jetons de la place 1, ou vider la place 2. Maxime choisit de changer de transition et vide la place 2 pour la place 4 (où aboutit un jeton). Puis il ne reste qu’une transition activable, ce qui fait passer à 1 le nombre de jetons restants en place 1 et ramène un autre jeton en place 2 :
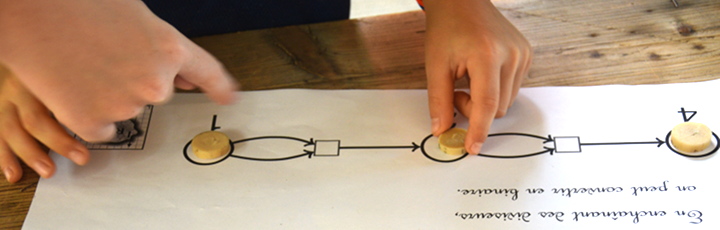
L’écriture binaire de 7 est donc 111.
Celle de 2 est 010 :

Trois, en binaire, s’écrit 011 :
Quelques minutes ont suffi à Maxime pour écrire en binaire tous les nombres de 1 à 7.
Ces activités sont intéressantes parce que le sujet (réseaux de Petri) n’est connecté de façon évidente à aucune notion vue au programme, et elles peuvent donc être traitées indépendamment de la progression. Elles sont fortement basées sur la manipulation et peuvent donc même servir à introduire des notions vues plus tard en cours (infini potentiel, algorithme d’Euclide, vecteurs, équations à plusieurs inconnues...). Elles sont ludiques donc susceptibles d’intéresser tous les élèves (et leurs enseignants). Elles favorisent le lien social via la travail collaboratif (on ne joue pas l’un contre l’autre mais seul ou collaborativement). Mais elles sont chronophages et il aurait fallu bien plus de temps que la demi-heure allouée pour permettre aux élèves de jouer vraiment (et pas seulement apprendre la règle du jeu). Un temps long consacré à ces activités serait cependant bien moins efficace qu’une séquence pédagogique en plusieurs séances (club durant l’année, voire les années) allant de la découverte du jeu en CM1 (voire avant, à expérimenter) jusqu’à sa modélisation Python en terminale.
Il est important de favoriser l’activité « nuage de mots » et surtout la création de réseaux de Petri comme le montrent les exemples faits en 6e ci-dessus.


























Commentaires