Note après la publication de la version 3.5
Cet article a été écrit en septembre 2009. Depuis avril 2010 et la version 3.5, les scripts peuvent être inclus dans la figure.
Le contenu de cet article présente les bases des CarScript, mais on profitera des classeurs et des scripts dans les figures en consultant aussi ce lien qui contient plus de 50 scripts dont ceux de cet article
Cet article est rédigé à la fois pour présenter les possibilités des CaRscripts de CarMetal, mais aussi pour être utilisée en parallèle avec le logiciel CaRMetal dans sa version 3.1.1 ou ultérieure. C’est la raison pour laquelle les premiers onglets ne contiennent aucun applet java mais seulement des copies d’écran. Les scripts sont présentés à la fois en copie d’écran et en code à copier-coller dans l’éditeur, en général dans un bloc dépliable à cliquer. Les derniers onglets proposent les résultats obtenus en manipulation directe.
Si des figures sont nécessaires à l’utilisation d’un script, elles sont téléchargeables en fin d’article. Les figures produites le sont aussi. L’article est structuré en onglets selon l’organisation suivante :
Introduction : Découverte de l’interface. Présentation de l’organisation possible de ses scripts. L’intérêt des Carscripts.
Construction : Sur l’exemple élémentaire de l’orthocentre d’un triangle, nous abordons l’utilisation des outils comme fonction ou comme procédure.
Tournesol : Une première boucle d’abord statique en javascript « pur » puis ensuite avec une dimension dynamique en CarScript. Premières explorations de la syntaxe.
Euler : Mise en place d’un algorithme universel pour la méthode d’Euler, avec une fonction CaRMetal comme paramètre. Second niveau d’exploration de la syntaxe.
Toile : La toile d’araignée des suites récurrentes. Application des connaissances développées aux deux onglets précédents. Nouvel exemple de script générique applicable à toutes les fonctions.
Syntaxe : Un premier bilan de ce qui a été fait jusqu’ici est résumé dans cet onglet. C’est aussi l’occasion de proposer d’autres explorations sur la syntaxe.
Manipulations : Les figures précédentes, finalisées dans des applets.
L’expérience en formation (PDF téléchargeable en fin d’article) montre que la réalisation à la main de toutes les figures de ces onglets prend un peu moins de 3 h. Le copier coller des scripts comme proposé ici fait largement gagner du temps. Mais se tromper sur la syntaxe fait réfléchir aussi ...
Introduction
1. Découverte de l’interface - Organisation des scripts
Dans le menu principal de CaRMetal si on clique sur Javascript/ ouvrir l’éditeur de script , on a à sa disposition l’interface suivante :
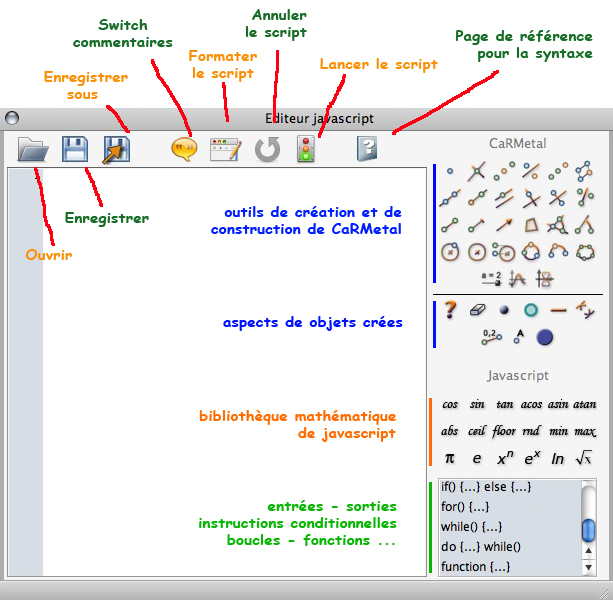
La fenêtre d’édition est surmontée d’une barre d’icones :
- un premier groupe de trois icones pour l’ouverture et l’enregistrement de scripts
- un deuxième groupe de 4 icones composé
- d’un switch « commentaire » qui transforme un texte en commentaire ou l’inverse
- d’un outil de formatage du script
- d’une annulation (multiple) de l’exécution des scripts
- d’un bouton de lancement du script
- une dernière icone renvoie à l’aide en ligne, actuellement en anglais. Rappelons qu’à la page de présentation de ce dossier sur les CarScripts, Alain Busser propose un manuel de référence de 56 pages qui reprend l’aide en ligne largement illustrée d’exemples que l’on peut utiliser par copier coller.
Déjà les habitués du javascript apprécieront les points 3 et 4 du deuxième groupe d’icones.
La partie droite est divisées en trois parties. Bien entendu, toutes les fonctions de la bibliothèque mathématique sont disponibles ainsi que toutes les instructions usuelles du javascript, les boutons correspondent aux plus usuelles pour une utilisation au lycée.
Si on le souhaite on peut copier le code proposé ci-dessous pour l’exécuter. Mais, pour cet exemple, il est plus intéressant de cliquer soi-même sur les boutons de l’éditeur pour voir son fonctionnement. Nous laissons au lecteur le soin d’imaginer ce que fait le script avant de le lancer.
for (i=0; i<20; i++){
x=2*Math.cos(Math.PI*i/10);
y=2*Math.sin(Math.PI*i/10);
p=Point(x,y);SetHide(p,true);
c=FixedCircle(p,2);
SetColor(c,"green");
}On note en particulier que les items disponibles proposent en général une interaction implicite avec la figure. Si vous cliquez sur les icones de l’éditeur, vous devez ajuster les variables. Par exemple l’item de cercle fixe (FixedCircle) propose par défaut un point (éventuel) de la figure comme centre.
Tout ceci sera largement détaillé à l’onglet suivant.
Organisation de ses scripts
Cette partie est réservée à une seconde lecture, lors d’une utilisation intensive des scripts. Il s’agit d’organiser ses scripts dans des dossiers. Pour cela on observe que tant que l’on n’a pas défini un dossier de script, le menu javascript est le suivant :
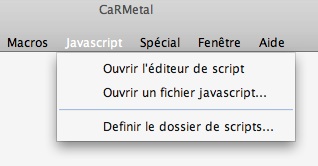
On peut alors préparer un dossier de script, dans lequel on peut ajouter des dossiers internes (modifiables ensuite comme on le souhaite bien entendu. Et une fois que ce dossier a été choisi, le menu javascript s’enrichit de ces dossiers, éventuellement imbriqués :
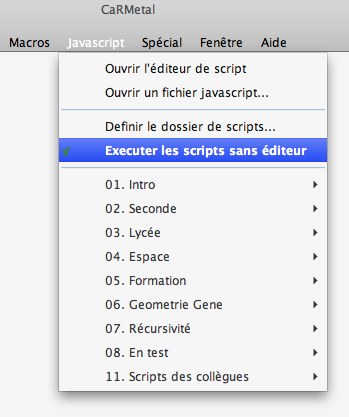
Construction
2. Un premier script géométrique - Approche fonctionnelle et procédurale
Commençons par construire, en script, l’orthocentre d’un triangle
a) Prendre trois points (en cliquant sur l’icône point). Ils se présentent sous la forme fonctionnelle :

c’est à dire que Point est une fonction qui renvoie une variable JavaScript de type chaine de caractère r dont le contenu est le point (pour une première représentation). Les coordonnées ne sont qu’une initialisation.
b) Renommer les variables a, b et c. Puis exécuter ce script. Vérifier que l’on peut déplacer les points produits et, par clic-droit sur les points, qu’ils ne se nomment pas du tout a, b, et c, ni A, B, et C, mais probablement P1, P2, P3 (nommage interne par défaut).
c) Poursuivons en créant les côtés du triangle
Avant cela on peut annuler le lancement du premier script (mais on peut le faire juste avant de le lancer à nouveau par la suite). On utilise l’icône de segment qui produit une ligne comme

où E et K, entre guillemets, sont des noms de points éventuels de la figure, mis par défaut au hasard, sans rapport avec la figure. On modifie cette ligne en mettant à la place de ces noms de points , les variables JavaScript précédentes, sans guillemets, pour obtenir (utiliser le copier-coller) :

On peut à nouveau lancer le script (après avoir annulé l’effet du précédent) et vérifier qu’en déplaçant les points le segments se comportent comme attendu. Annuler à nouveau le script pour continuer.
d) construction des hauteurs et de l’orthocentre
On poursuit par l’utilisation de l’icône perpendiculaire. On remplace donc une expression générique de type

par les trois hauteurs, exprimées en fonction des variables JavaScript de la figure (indiquer d’abord la droite ou le segment, puis le point)

Et on termine par l’intersection en modifiant ce que donne l’icône d’intersection par
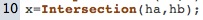
On a donc construit l’orthocentre d’un triangle en 10 étapes à partir d’une feuille blanche.
Lancer le script pour vérifier que l’on obtient ce qui était prévu et que la figure suit bien la manipulation directe sur les trois points de base. Vérifier ensuite que les perpendiculaires ont des noms internes au logiciel (perp1, etc).
Approche fonctionnelle et approche procédurale
On remarquera que ce script n’utilise que des variables JavaScript pour construire la figure. Les items utilisés sont alors des fonctions JavaScript qui renvoient un nom de variable (en fait toujours une chaine de caractère). On peut remarquer que l’on engage le même processus quand on écrit « soit d1 la parallèle à d passant par A » : on y sous entend que d1 est une droite et que A est un point, et l’on utilise le noms des objets pour les désigner.
La principale différence avec les textes des programmes de construction est que les points de la figure ne s’appellent pas a, b, c ni les droites hA, hB, hC. Ce type de script (fonctionnel) invite à une certaine distance par rapport aux objets qui sont tout de suite des variables. On peut considérer cela formateur, et aller dans ce sens, en favorisant ce type de scripts pour les constructions géométriques. On peut aussi juste n’y voir qu’une pratique naturelle d’un langage de programmation.
D’autres y trouveront un prétexte pour refuser cette approche, jugée assez éloignée d’une certaine pratique de classe. Il est alors intéressant de voir que les mêmes outils fonctionnels permettent d’avoir une approche uniquement procédurale, plus proche de la description des programmes de construction (de type chek list).
En effet les fonctions géométriques des Carscripts autorisent de nommer les objets. On peut donc travailler sur une figure géométrique dynamique où les points sont explicitement nommés. Par ailleurs il n’est pas nécessaire d’avoir cette approche fonctionnelle des objets géométriques (u=Point( …)). Les fonctions géométriques ajoutées au JavaScript se comportent aussi comme des procédures.
Reprenons le même script avec une approche purement procédurale :
Les points sont nommés : A, B et C sont les noms des points dans la figure, de même pour les segments. Ceux-ci sont définis directement par les noms des points.

On peut lancer ce premier script. A nouveau, les noms des points ne sont pas affichés, mais par un clic droit on peut vérifier qu’ils s’appellent bien A, B, et C. Pour voir les noms des points, il faudrait ajouter l’instruction

D’une manière générale, ce qui est entre guillemets se réfère directement à des objets de la figure.
Poursuivrons dans ce style procédural :
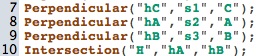
Les hauteurs s’appellent hA, hB, et hC comme on peut le vérifier en lançant le script (faire clic-droit sur les hauteurs pour voir les noms)
Dans cette approche les fonctions géométriques de JavaScript se comportent comme des procédures. On utilise alors les noms effectifs des objets produits par les outils antérieurs pour préciser sur quels objets s’opère la procédure. La démarche est de fait plus opérationnelle et la précédente clairement plus conceptuelle.
Bien-sûr, il est possible de mélanger les deux approches, par exemple une écriture comme u= Point(« A », 4, 2) est valide : on comprend bien que la rencontre des deux approches va permettre une souplesse particulièrement riche, surtout dans des boucles comme nous allons le voir dans le prochain onglet.
Premier exercice d’application
Ajouter au script précédent le cercle circonscrit au triangle (avec son centre) et le centre de gravité, puis tracer la droite d’Euler. Jouer avec les couleurs pour mettre les droites de type différent dans des couleurs différentes. Les couleurs de base sont par défaut « blue », « red », « green », « brown », « cyan », « black ».
Autre exercice d’application
éventuellement pour une seconde lecture ... même si le code est proposé.
Nous allons faire, dans un cas simple, une figure déjà construite à cette page dans un contexte un peu plus riche, pour illustrer que l’outil de cercle de rayon fixe est en fait un outil de cercle de rayon fonctionnel.
On se donne un cercle $c_1$ de centre $O_1$ et un point intérieur $O_2$. Par un point M appartenant au cercle $c_1$ on veut construire un triangle MNP dont $c_1$ est le cercle circonscrit et $O_2$ le centre du cercle inscrit. Autrement dit MNP est inscrit dans $c_1$ et circonscrit à $c_2$. La figure de départ est donc la suivante :

On notera$s_1$ le segment $[O_1O_2]$ qui, même s’il n’est pas indispensable, est pratique pour avoir la distance entre les deux points : dans CaRMetal, le nom d’un segment est aussi une variable qui contient sa longueur.
Et le résultat, déjà utilisé pour présenter l’outil cercle fixe est rappelé en commentaire introductif de ce CarScript :
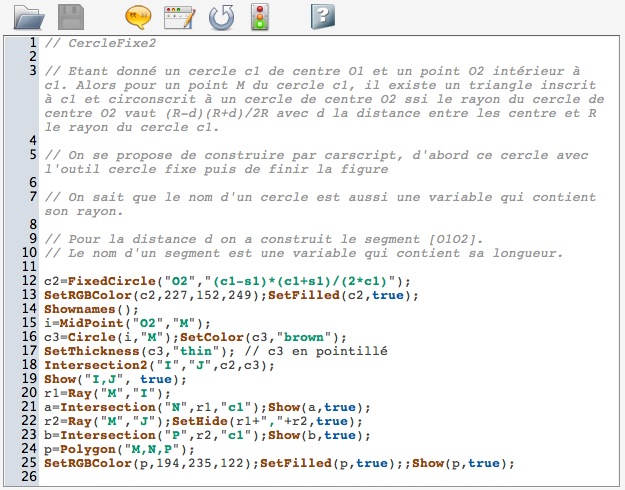
On remarquera que le cercle fixe a pour rayon une expression CaRMetal qui utilise à la fois les variables $c_1$ et $s_1$. On aurait pu aussi prendre une expression de CaRMetal pour calculer la distance entre les deux centres et utiliser cette expression. Les outils appelés sont ceux du logiciel ainsi on n’est pas surpris que la demi-droite d’origine M passant par I coupe le cercle $c_1$ en le point cherché (P) et non pas M, car c’est le comportement ("intelligent", ie qui correspond à l’engagement direct attendu) du logiciel.
Le CarScript donne la figure suivante :
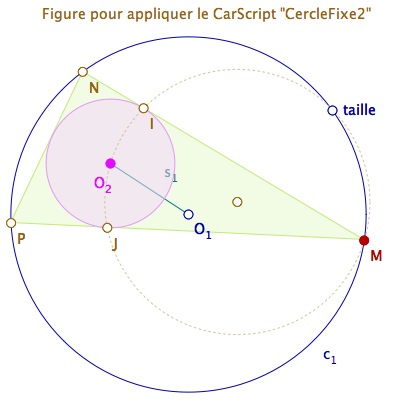
Bien entendu, le script n’apporte rien de plus que les possibilités de constructions usuelles, dans le cas précis de cette figure, mais il montre comment prendre et traiter les données d’une figure.
Remarquons tout de même que ce script est, en fait, un programme de construction classique appliqué à des donnes qui correspondent aux hypothèses. Le langage étant élémentaire - même s’il est en anglais - on peut envisager de travailler parfois les programmes de constructions en classe avec cet outil, par exemple pour valider des productions d’élève lors d’un bilan d’activité.
Tournesol
3. Une première boucle - Du statique au dynamique (a)
Utilisation des boutons de l’éditeur pour la bibliothèque Math de JavaScript
Dans cet onglet, nous allons faire tout d’abord un script que l’on peut qualifier d’une certaine façon de statique, puis le transformer en une figure réellement dynamique. Quitie à apprendre un outil, autant le faire en faisant de belles figures, ici nous allons faire le coeur d’un tournesol : on dessine une suite de points $P_k$ en coordonnées polaire, avec un rayon $r=c \sqrt(k)$ et un angle $t=i \theta_0$ où $\theta_0$=137,5°, angle de base (approximation de $\frac{2\pi}{1+\Phi}$) sur lequel nous allons mettre une variation bien entendu. On notera que c’est un vocabulaire (coordonnées polaires) et un contexte (suites) accessibles en 1°S. L’idée est de faire un travail sur les boucles qui a un résultat graphique attrayant. Par ailleurs, c’est un (micro-bout d’) algorithme utilisé dans les logiciels d’animation (on peut télécharger ce livre - abop.pdf 240 pages 17 Mo - et voir les pages du fichier pdf 112 et suivantes).
3.a. Version javascript
On utilise bien entendu les fonctionnalités de l’éditeur de script de CaRMetal, en particulier pour appeler les fonctions trigonométriques que nous n’avons pas à taper.
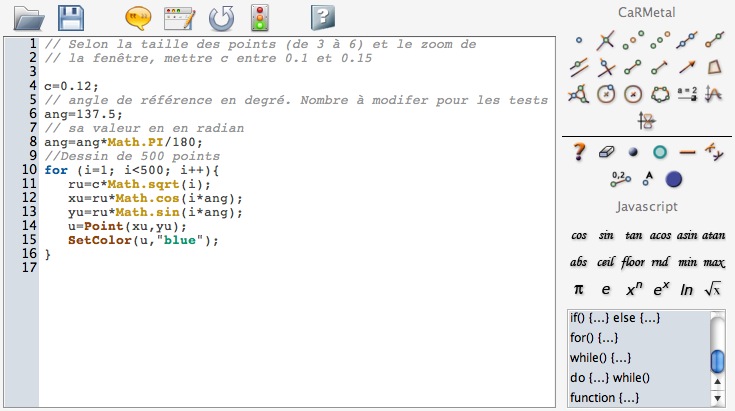
Ce qui donne le dessin suivant

déjà sympathique pour un premier essai.
Copier le script
// Selon la taille des points (de 3 à 6) et le zoom de
// la fenêtre, mettre c entre 0.1 et 0.15
c=0.12;
// angle de référence en degré. Nombre à modifier pour les tests
ang=137.5;
// sa valeur en en radian
ang=ang*Math.PI/180;
//Dessin de 500 points
for (i=1; i<500; i++){
ru=c*Math.sqrt(i);
xu=ru*Math.cos(i*ang);
yu=ru*Math.sin(i*ang);
u=Point(xu,yu);
SetColor(u,"blue");
}Remarquer que la sélection du pointeur fait surligner tous les points : chaque point produit est modifiable à la souris, on n’a fait que les initialiser à la position voulue. En particulier cliquer sur un point pour voir ses coordonnées : elles sont numériques. Nous avons fait un dessin. C’est en ce sens que l’on peut dire que la figure n’est pas dynamique car, même si on peut déplacer chaque point, on a pas produit une figure qui n’a d’autre cohérence d’ensemble que ce dessin produit. On se propose d’améliorer cela.
Mais avant quelques commentaire sur ce premier script :
La programmation en JS ressemble à celle d’une calculatrice, on utilise des variables, d’abord ru (pour éviter deux fois ce calcul), puis xu et yu, ce qui permet de placer un point. Il a fallu écrire l’angle en radian pour utiliser les lignes trigonométriques usuelles.
Après l’avoir annulé, on peut relancer le script en prenant d’autres valeurs pour l’angle de référence (137,6° ou 136,3°).
Dans une boucle, on évite de nommer le point de manière non indexée à l’indice (ie on évite d’écrire u=Point("A",xu,yu)) sinon le nom se duplique et CaRMetal produit des noms de points étoilés A, A*, A** etc ... ce qui devient vite ingérable comme dans l’exemple de ce bug (que chacun fait un jour) :

3.b. Version Carscript
On souhaite désormais transformer ce dessin en une figure dynamique où, par exemple, l’angle sera modifiable par un curseur. Cela veut dire que l’angle est un paramètre de chaque point et qu’il doit être conservé, comme variable, afin que chaque point réagisse au déplacement du curseur. Il faut donc une approche différente.
Comme on l’a laissé entendre un peu plus haut, à propos des noms de points, JavaScript communique avec CaRMetal par des chaines de caractères. Les paramètres dynamiques des objets (ici simplement les coordonnées des points) sont transmis au travers des chaines de caractères qui utilisent les fonctionnalités mathématiques du logiciel et les variables propres à la figure. C’est la gestion complexe de tout cet environnement qui apporte une véritable nouveauté en géométrie dynamique.
Il faut alors transmettre les variables JavaScript autrement. Elle seront transmises par leur contenu : si k est une variable (par exemple de boucle), pour la transmettre à CaRMetal on utilisera son contenu _k. Pour une variable de boucle _k est seulement sa valeur numérique, mais le contenu d’une variable peut être plus riche – et en particulier dynamique - c’est pour cela qu’on évite de parler de transmission de la valeur. Voyons ce que cela donne pour le tournesol dynamique.
Commencer par créer un curseur d’expression, nommé ang qui ira de 135 à 140 selon la démarche suivante (d’abord dans l’onglet "Construction" de la palette d’outils).

Puis on lui applique le script suivant (commenté plus bas) :

ce qui donne :
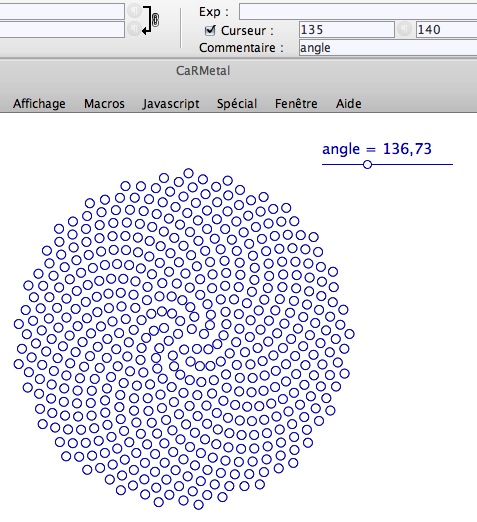
– les coordonnées du point construit sont passées dans deux chaines de caractères.
– les variables JavaScript c et i sont passée par contenu _c et _i dans les chaines.
– dans les chaines de caractères, nous sommes dans CaRMetal, et pas en JavaScript :
– les fonctions sont celles de CaRMetal : sqrt et pas Math.sqrt,
– cos et sin sur un angle en degré car c’est le fonctionnement de CaRMetal (ce serait rcos et rsin pour les angles en radian)
– la variable de la figure ang est utilisée comme telle, multipliée par _i.
Copier le script
c=0.12;
for (i=1; i<500; i++){ u=Point("_c*sqrt(_i)*cos(_i*ang)","_c*sqrt(_i)*sin(_i*ang)");
}Clic-droit sur un point pour voir ses coordonnées : elles ne sont plus numériques mais bien algébriques, fonction de la variable ang.

On peut aussi choisir d’augmenter la taille des points, comme ici :

On a utilisé une approche fonctionnelle pour le point avec la variable u. Cela n’était pas nécessaire bien entendu. Mais c’est utile si on veut faire varier les couleurs des points sans avoir à les nommer : une fois le script précédent testé, rajouter dans la boucle cette ligne pour la couleur :

Ce qui donne ceci :
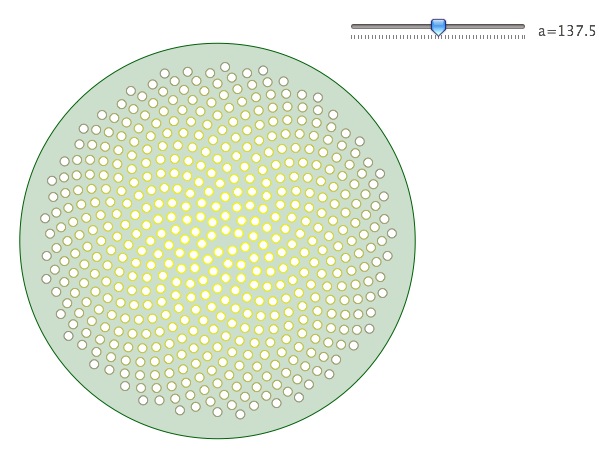
Remarque à propos du curseur système de l’illustration
Plus haut on a invité à l’utilisation d’un curseur d’expression plutôt qu’un controle système comme dans cette illustration. Il n’y a pas de différence, sauf un petit bug (pour le moment en 3.1.1 qu’il faut connaître : quand on utilise un curseur système il faut éviter d’interrompre inopinément un script long alors que c’est sans effet sur une expression. Quand on débute ; selon les machine, on peut ne pas voir que le script continue de s’exécuter et l’arreter avant la fin.
Les points ont tous la même taille mais la saturation jaune au centre donne un effet de flou gaussien qui modifie la vision et peut faire croire que les points au centre sont plus gros.
Copier le script
// Selon la taille des points (de 3 à 6) et le zoom de
// la feuille, mettre c de 0.1 à 0.15
c=0.12;
for (i=1; i<500; i++){ u=Point("_c*sqrt(_i)*cos(_i*ang)","_c*sqrt(_i)*sin(_i*ang)");
SetRGBColor(u,250-Math.round(i/5),250-Math.round(i/5),Math.round(i/4));
}On peut s’essayer à d’autres variantes sur les couleurs entre respectant qu’elles doivent aller de 0 à 255 bien entendu.
Pour terminer avec tournesol, signalons un article (savant) sur la question de Xavier Caruso sur cette page (dans Autres articles (publié dans RMS)
Résumé de ce qui a été vu dans cet onglet
• Les informations dynamiques, dépendant des données de la figure, se transmettent toujours dans une chaine de caractère.
• À l’intérieur d’une chaine, la programmation utilise les expressions usuelles de CaRMetal.
• On passe les variables javascript par leur contenu (par exemple une valeur numérique dans le cas d’une boucle), on utilise une syntaxe spécifique : la variable k est utilisée dans une chaine par l’expression _k.
• Toutes les fonctions géométriques de CaRMetal rajoutées au javascript renvoient une chaine de caractère : le nom de l’objet.
Il reste encore une fonctionnalité importante à découvrir, ce que nous allons faire au travers d’une autre civité de 1°S : la primitivation par le méthode d’Euler
Documents joints
-
- TP Apprentissage CarScripts
- Reprend l’essentiel de cet article pour une utilisation en formation continue
Erreur d’exécution plugins/auto/sarkaspip/v4.1.0/noisettes/document/inc_images_jointes.html




Commentaires