Construction du nombre en λ-calcul

mercredi 27 mai 2015
par  Alain BUSSER , Florian TOBÉ

La théorie des systèmes dynamiques, qui souvent concerne les systèmes dynamiques discrets par l’application de Poincaré, étudie les propriétés de l’orbite d’un objet dans une action de groupe (mathématiques). Par exemple, les itérées de la fonction successeur qui à x associe x+1, transforment le nombre 0 en l’ensemble des entiers naturels (l’orbite de 0). L’idée de considérer non l’orbite par l’action du groupe (ici un semi-groupe, N), mais plutôt le (semi-)groupe lui-même, est à l’origine de la représentation des entiers dans le λ-calcul (Kleene et Church).

On peut donc voir dans les entiers de Church une manière de représenter les nombres non plus comme des objets mais comme des actions. Et comme on le verra, la subitisation peut s’expliquer par la nécessité d’utiliser un itérateur pour des nombres suffisamment grands avec le classement suivant des entiers :

  • zéro (apparaît tardivement)
  • un (et son contraire « plusieurs »)
  • deux
  • trois
  • beaucoup (c’est-à-dire atteignables par l’itérateur)

Systèmes dynamiques discrets

Un exemple de système dynamique simple et typique est le système non chaotique suivant :

  • on choisit un nombre de départ (par exemple 255/256)
  • on l’élève au carré (c’est-à-dire qu’on le transforme par la fonction « élévation au carré »)
  • on recommence
  • et encore
  • et encore...

Ce système dynamique est assez simple à programmer en Sophus :

graine = new Variable 255/256
4.foisFaire ->
    élever graine, auCarré
    montrer graine

En le faisant tourner, on a les affichages (arrondis) suivants :

nombre de répétitions résultat
1 0,992
2 0,984
3 0,969
4 0,939

Et si préfère aller plus vite en construisant l’orbite et en n’affichant que celle-ci à la fin, on modifie le script en conséquence, en modélisant l’orbite comme un tableau dans lequell on empile au fur et à mesure les valeurs successives de la graine :

graine = new Variable 255/256
orbite = [graine.valeur]
10.foisFaire ->
    élever graine, auCarré
    orbite.empiler graine.valeur
montrer orbite

On peut voir ce système dynamique de deux manières différentes :

  1. L’orbite de 255/256 est un ensemble dénombrable, muni d’une relation d’ordre (l’inverse de l’ordre naturel), d’une addition ($\left( \left( \frac{255}{256}\right )^{2^a}\right) ^{2^b}=\left( \frac{255}{256}\right )^{2^{a+b}}$) etc, est un modèle de l’arithmétique (isomorphe à N) ;
  2. L’ensemble des itérées de la fonction « carré » est un semi-groupe isomorphe à N

Or le second modèle est non seulement plus simple que le premier, mais également indépendant de la valeur initiale de la graine (si celle-ci vaut 1, la suite est constante et ne peut plus être en bijection avec N). Il est même indépendant de la fonction que l’on itère et ne nécessite plus que celle-ci soit bijective, chaotique ou pas chaotique.

Une façon simple de représenter les entiers comme orbite d’un système dynamique est de prendre pour fonction à itérer, la fonction « successeur » (ou toute fonction de la forme x+C qui donne une suite arithmétique) :

graine = new Variable 0
orbite = [0]
10.foisFaire ->
    incrémenter graine
    orbite.empiler graine.valeur
montrer orbite

Ou une fonction linéaire, donnant alors une suite géométrique (dans ce cas l’isomorphisme avec N est exponentiel, ça illustre d’autres chapitres des mathématiques) :

graine = new Variable 100
orbite = [graine.valeur]
10.foisFaire ->
    diminuer graine, de, 2, pourcents
    orbite.empiler graine.valeur
montrer orbite

En fait même lorsque la suite n’est pas monotone, c’est une suite donc son image est isomorphe à N ; ici les itérées de la fonction cosinus :

graine = new Variable 0
orbite = [graine.valeur]
10.foisFaire ->
    mettreDans graine,cos graine.valeur
    orbite.empiler graine.valeur
montrer orbite

Peano

Les axiomes de Peano construisent les entiers à partir de 0 et la fonction successeur. Avec alcoffeethmique on peut programmer quelque chose comme ceci :

succ = (x) -> x+1
un = succ 0
deux = succ un
trois = succ deux
affiche trois

Alors, en notant s la fonction successeur, on prédéfinit 0 (comme fait ci-dessus) et on définit les autres par

  • 1 = s(0)
  • 2 = s(1)=s(s(0))
  • 3=s(s(s(0)))

Et ainsi de suite : On reconnaît bien là une représentation en base 1, le nombre n étant représenté par n fois la letrre s :

succ = (x) -> x+1
un = succ 0
deux = succ succ 0
trois = succ succ succ 0
affiche trois

Les entiers de Church consistent essentiellement à généraliser cette notation à d’autres fonctions que la fonction sucesseur. Ce qui va être fécond, puisque par exemple on peut calculer une addition dans l’arithmétique de Peano :

succ = (x) -> x+1
pred = (x) -> x-1
addition = (x,y) ->
    if y is 0
        x 
    else 
        succ addition x, pred y
affiche addition 3, 4

On peut aussi définir la multiplication :

succ = (x) -> x+1
pred = (x) -> x-1
mult = (x,y) ->
    if y is 0
        0 
    else 
        x + mult x, pred y
affiche mult 3, 4

Ces définitions sont utiles pour démontrer les propriétés de ces opérations, comme par exemple leur commutativité. On constate qu’elles font toutes deux usage du fait que seul 0 n’a pas de prédécesseur.

Russel

Dans les Principia mathematica, Whitehead et Russel modélisent les entiers par des ensembles (ou plus précisément leurs cardinaux), sur l’équivalence que voici :

  • 0 = {}
  • 1 = { 0 } = { { } }
  • 2 = { 0, 1} = { { },  { { } } }
  • 3 = { 0, 1, 2 } = {  { } ,  { { } }, { { },  { { } } } }

etc.

On voit donc là encore une numération unaire à l’œuvre, mais le nombre $n$ n’est pas représenté par $n$ accolades ouvrantes, mais par $2^{n}$ accolades ouvrantes.

Noter que, alcoffeethmique gérant les ensembles, on peut retrouver les notations ci-dessus avec ce script :

zero = new Ensemble []
un = new Ensemble [zero]
deux = new Ensemble [zero,un]
trois = new Ensemble [zero,un,deux]
affiche trois

Et afficher mieux les entiers ainsi construits peut se faire par les cardinaux :

zero = new Ensemble []
un = new Ensemble [zero]
deux = new Ensemble [zero,un]
trois = new Ensemble [zero,un,deux]
affiche trois.cardinal()

Cela sera utilisé plus bas pour les reconnaisseurs d’entiers (ou de cardinaux) en λ-calcul.

Représentation

Ainsi, le nombre n supérieur à 1 est représenté en λ-calcul par la fonctionnelle qui, à toute fonction f, associe sa n-ième itérée :

  • 1 associe à f, la fonction f elle-même ;
  • 2 associe à f, la fonction f∘f
  • 3 associe à f, la fonction f∘f∘f

Etc. Church ne définissait pas le nombre 0, mais la théorie des systèmes dynamiques définit un prequel à cette suite : La fonctionnelle qui, à une fonction f, associe l’identité. Avec les notations du lambda-calcul, on note λx.x l’identité et λf.F la fonctionnelle F. Alors

  • 0 associe à f, la fonction qui à x associe x : λf.λx.x
  • 1 associe à f, f elle-même, c’est—à-dire λx.f(x) ce qui donne λf.λx.f(x) [1]
  • 2 associant à f, f∘f soit la fonction qui, à x, associe f(f(x)), soit λx.f(f(x)), est représenté par la λ-expression λf.λx.f(f(x))

Le nombres allant de 0 à 5 sont stockés dans le jeu des alligators sous forme de λ-expressions. Il suffit de faire apparaître le clavier puis cliquer sur une des touches numériques. Chaque λf est alors représenté par un alligator de couleur marron, et chaque λx par un alligator bleu. Alors λf.λx.x est dessiné sous la forme d’un alligator marron surmontant un alligator bleu surmontant un œuf bleu :

Le nombre 1 ressemble au nombre 0 à ceci près que comme on a remplacé x par f(x) on rajoute, devant l’œuf bleu, un œuf marron :

Pour le nombre 2 on rajoute un autre œuf marron devant le premier œuf marron. Mais alors doit-on interpréter le résultat comme f(f)(x) ou comme f(f(x)) ? Le deuxième évidemment mais il a fallu rajouter autour de f(x) des parenthèses, qui sont représentées par un alligator blanc au-dessus de f(x) :

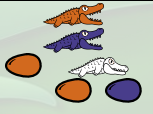
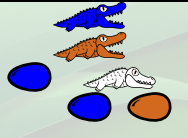
Plus généralement le nombre n est représenté par n œufs marron dans une configuration similaire à celle ci-dessus : Surmonté de n-1 alligators blancs, le dernier ayant un œuf bleu à manger, le tout surmonté d’un alligator marron et d’un alligator bleu. Le nombre 3 :

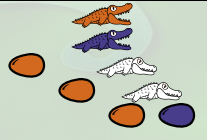
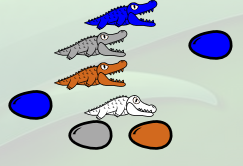
Le nombre 4 :

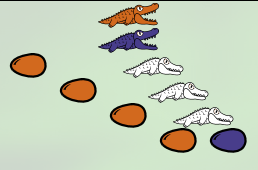
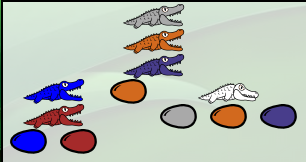
Le nombre 5 avec ses 5 œufs marron :

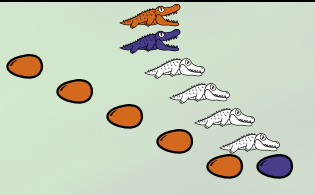
Pour entrer le nombre 8, il suffit donc de mettre dans le clavier la λ-expression suivant puis de la dessiner :

λf.λx.(f(f(f(f(f(f(f(f x))))))))

On peut aussi par exemple multiplier 4 par 2, en effet il est possible d’effectuer des calculs par le λ-calcul : Voir les onglets suivants.

revenir aux onglets

Successeur

Puisqu’un entier n est représenté par la fonctionnelle qui, à f, associe la n-ième itérée de f, le successeur est la fonctionnelle qui, à une telle fonctionnelle, associe la fonctionnelle qui, à f, associe f∘n. Cette fonctionnelle se note

λn.λf.λx.f (n (f x))

et sa représentation dans le marais des alligators est celle-ci :

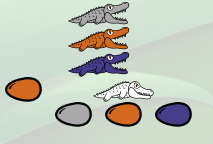
Voici par exemple comment le λ-calcul permet de vérifier que le successeur de 4 est bien 5 :

On entre les expressions correspondant au successeur et à 4 (on a renommé les x en y et les f en g dans l’expression du successeur) :

λn.λg.λy.g (n g y)

λf.λx.(f(f(f(f x))))

La lambda-expression à réduire est juste leur concaténation :

(λn.λg.λy.g (n g y))  (λf.λx.(f(f(f(f x)))))

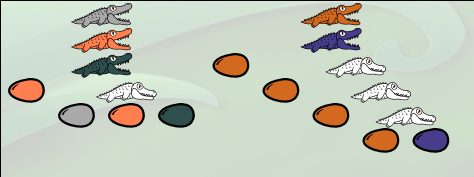
L’alligator gris a toute la famille représentant le nombre 4 devant lui. Il va donc la dévorer, et l’œuf gris étant en-dessous de lui va éclore en donnant un clone de toute la famille :

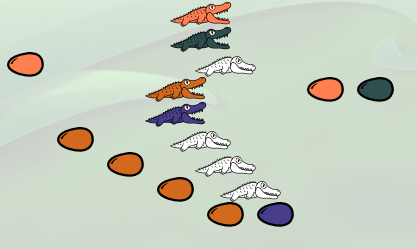
On constate que, suite à une indigestion, l’alligator gris a disparu. L’expression obtenue est alors

λg.(λy.(g (λf.(λx.(f(f(f(f x ))))) g y)))

La suite de l’histoire va être l’ingestion par l’alligator marron, de l’œuf saumon qui est devant lui. Il surmonte 4 œufs marron, donc chacun va virer au saumon, donnant l’expression suivante :

λg.(λy.(g (λx.(g(g(g(g x )))) y )))

On voit maintenant 5 œufs saumon qui représentent le successeur de 4 :

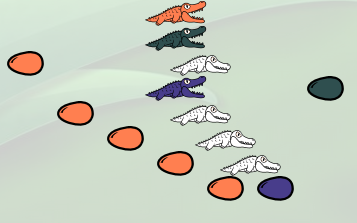
Ensuite l’alligator bleu va manger l’œuf foncé qui est devant lui. Ce qui aura pour effet de transformer l’œuf bleu qui est en-dessous de lui, en œuf foncé : en mourant d’indigestion il laisse le nombre 5 comme on l’a vu dans l’onglet précédent :

λg.(λy.(g (λx.(g(g(g(g x)))) y)))

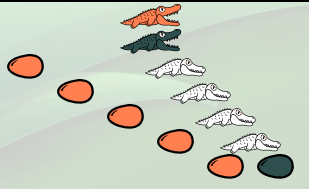
Le même genre de manip avec le jeu des alligators permet de vérifier que le successeur de 0 est 1, que le successeur de 1 est 2 etc, et surtout, pourquoi.

revenir aux onglets

Addition

Puisque 3 est représenté par f(f(f(x))) et 4 par f(f(f(f(x)))) alors leur somme s’obtient en remplaçant le x de 3 par 4. En langage croco ça donne ça :

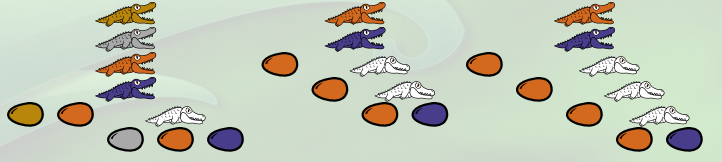
La λ-expression correspondante est

(λm.λn.λf.λx.m f (n f x)) (λf.λx.(f(f(f x)))) (λf.λx.(f(f(f(f x)))))

L’addition se fait comme ceci :

  • L’alligator λm (tout en haut à gauche) va manger la famille 3 (au milieu). Pour cela un renommage est nécessaire, en changeant les x et f en des a et b ; autrement dit, toute la famille change de couleur, suite à la peur, et devient rouge et bleue :

Puis l’alligator l’ingurgite et l’œuf tout à gauche éclot, donnant naissance à toute une famille représentant le nombre 3 (et au passage il disparaît du tableau, étant devenu inutile) :

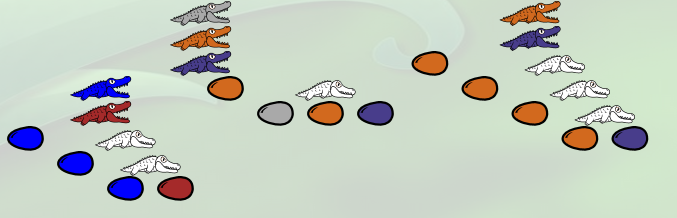
La λ-expression est devenue

λn.(λf.(λx.(λa.(λb.(a(a(a b)))) f (n f x)))) λf.(λx.(f (f (f (f x)))))

Maintenant c’est l’alligator gris qui va manger la famille 4, et celle-ci aussi, de peur, va changer de couleur (des c et des d à la place des f et des x) :

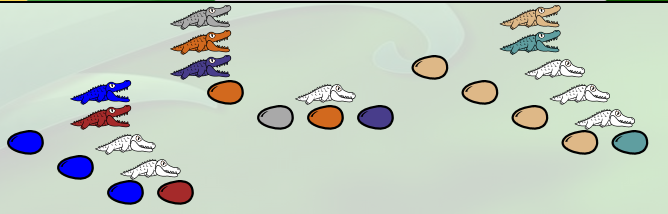
L’œuf gris va alors donner naissance à une famille « 4 » :

La λ-expression est maintenant devenue

λf.(λx.(λa.(λb.(a(a(a b)))) f (λc.(λd.(c(c(c(c d))))) f x)))

En fait, les familles 3 et 4 ont été déplacées et il y a maintenant 3 œufs bleus et 4 œufs couleur de sable. Mais si on regarde bien, les alligators de la même couleur qu’œufseux s’apprêtent chacun à manger un œuf orange, ce qui aura pour effet de colorier les œufs bleus et sable en orange et de les regrouper en une seule famille, c’est ainsi que l’addition sera faite.

D’abord c’est l’alligator bleu qui passe à table (et disparaît) :

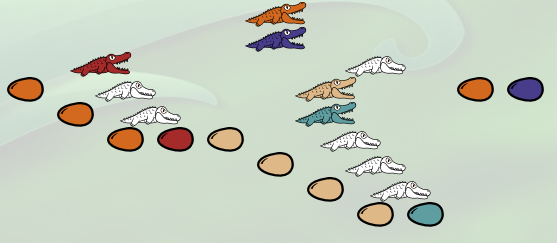
L’expression est devenue

λf.(λx.(λb.(f (f (f b))) (λc.(λd.(c(c(c(c d))))) f x)))

Puis le rouge :

En laissant l’expression

λf.(λx.(f (f (f (λc.(λd.(c(c(c(c d))))) f x)))))

Puis l’alligator couleur de sable :

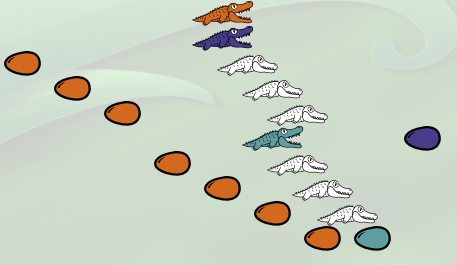
L’expression est alors

λf.(λx.(f(f(f(λd.(f(f(f(f d)))) x)))))

L’alligator cyan va maintenant manger un œuf bleu. Mais comme il n’y a qu’un œuf cyan en-dessous, celui-ci donne une copie de l’œuf bleu (et l’alligator cyan va juste disparaître du tableau de chasse) :

C’est bien une représentation du nombre 7, comme on peut le vérifer en comptant les œufs oranges ou en lisant la λ-expression obtenue :

λf.(λx.(f(f(f(f(f(f(f x))))))))

(là ce sont les « f » qu’il faut compter).

Remarque

La façon normale d’utiliser l’opérateur « plus » est de la faire suivre de deux numéraux de Church, comme l’a fait ci-dessus avec 3 et 4. Mais si on ne met que le numéral 1, on définit la fonction qui, à un numéral n, associe n+1, c’est-à-dire son successeur. Cela permet de retrouver l’opérateur « successeur » vu à l’onglet précédent.

Donc « plus un » s’écrit en λ-calcul

(λm.λn.λf.λx.m f (n f x)) (λf.λx.(f x))

et se dessine

Voici comment se déroule sa λ-réduction : Tout d’abord l’alligator brun va manger la famille « 1 » (qui va au passage changer de couleur). Comme pour toute addition, la famille « 1 » est maintenant protégée par l’alligator gris :

Le résultat provisoire s’écrit

λn.(λf.(λx.(λa.(λb.(a b)) f (n f x ))))

Ensuite l’alligator bleu va gober l’œuf orange ce qui va avoir pour effet de changer la couleur de l’œuf bleu en orange :

La λ-expression est maintenant devenue

λn.(λf.(λx.(λb.(f b) (n f x))))

Il reste encore une simplification possible : L’alligator acajou peut manger la famille à sa droite, la plaçant ainsi à droite de l’œuf orange :

On obtient bien la λ-expression « successeur » vue à l’onglet précédent, qui est, pour rappel

λn.(λf.(λx.(f (n f x))))

revenir aux onglets

Multiplication

Si 3 est représenté par g(g(g(x)))) et 4 par f(f(f(f(x)))) alors on multiplie 3 par 4 en remplaçant, chaque fois qu’elle apparaît, la lettre g par f(f(f(x)))) dans l’expression représentant 3. C’est donc juste une question de règles de réécriture. La fonctionnelle réalisant cette réécriture est

(λm.λn.λf.m (n f))

(m et n sont des entiers de Church et f la fonction à itérer m×n fois)

En langage crocodilien, il se représente ainsi :

Pour multiplier 3 par 4, on ouvre la console puis on clique successivement sur « MULT », « THREE » et « FOUR », ce qui donne la λ-expression suivante :

(λm.λn.λf.m (n f)) (λf.λx.(f(f(f x)))) (λf.λx.(f(f(f(f x)))))

Graphiquement :

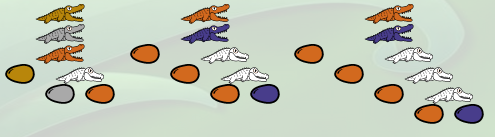
On peut, à l’aide du clavier, anticiper sur les recoloriages qui seront nécessaires, en renommant certaines variables ; l’expression devenant

(λm.λn.λf.m (n f)) (λg.λy.(g(g(g y)))) (λh.λz.(h(h(h(h z)))))

Soit, graphiquement :

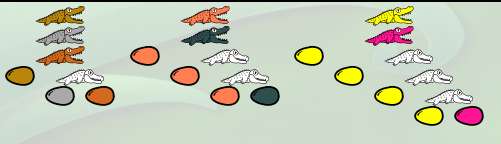
La première modification sera faite par l’alligator kaki, qui va, en substance, déplacer la famille 3 (saumon et sapin) sous la protection de son enfant orange (l’œuf kaki en-dessous de l’enfant orange, va éclore en donnant une copie de la famille « 3 ») :

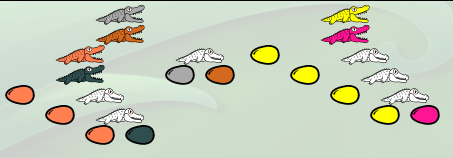
La λ-expression est alors devenue

λn.(λf.(λg.(λy.(g(g(g y)))) (n f))) λh.(λz.(h(h(h(h z)))))

Le suivant à satisfaire sa fin inextinguible est l’alligator gris, qui va lui aussi (parce qu’il y a un œuf gris en-dessous de lui) mettre (une copie de) la famille « 4 » sous l’alligator marron :

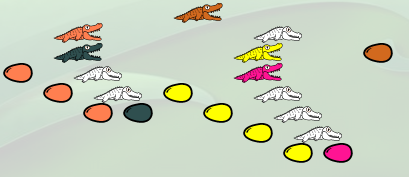
On obtient alors la λ-expression

λf.(λg.(λy.(g(g(g y)))) (λh.(λz.(h(h(h(h z))))) f))

Tout est maintenant en place pour que la multiplication puisse se faire : On voit que l’alligator de couleur saumon va manger la famille représentant le nombre 4, et comme cet alligator surmonte 3 œufs de couleur saumon, chacun d’entre eux va éclore donnant naissance à (une famille comportant) 4 œufs jaunes, ce qui dans les faits, effectuera le produit de 3 par 4. Le mot clé est « chaque » qui est à la base de l’idée de multiplication.

Une fois le repas effectué, il y a bien 12 œufs jaunes :

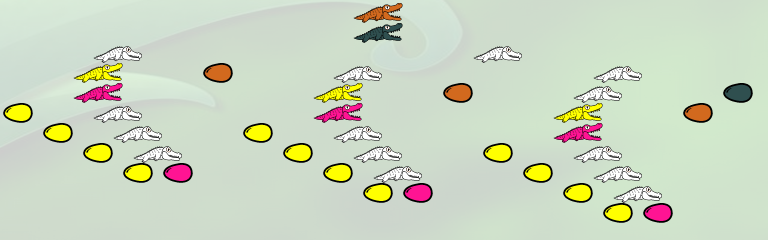
La λ-expression est maintenant devenue

λf.(λy.((λh.(λz.(h(h(h(h z))))) f) ((λh.(λz.(h(h(h(h z))))) f) ((λh.(λz.(h(h(h(h z))))) f) y))))

Le produit étant effectué, il ne reste plus que des simplifications à effectuer, notamment sous forme de regroupements. Tout d’abord l’alligator jaune de gauche va manger un œuf marron ce qui aura pour effet de colorier en marron les 4 œufs jaunes de gauche :

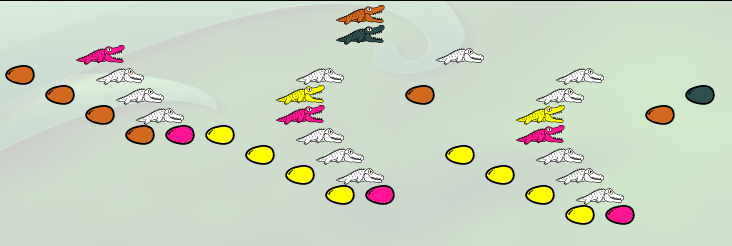
Après avoir enlevé les parenthèses devenues inutiles (ce qui s’est manifesté par le décès d’un alligator albinos), la λ-expression est devenue

λf.(λy.(λz.(f(f(f(f z)))) ((λh.(λz.(h(h(h(h z))))) f) ((λh.(λz.(h(h(h(h z))))) f) y))))

Ensuite l’alligator rose rapatrie les 8 œufs restants (avec leurs familles respectives) sous la protection de son enfant :

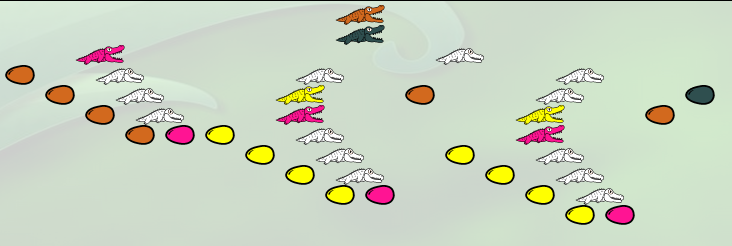
La λ-expression s’est alors provisoirement compliquée :

λf.(λy.(f(f(f(f(λh.(λa.((h(h(h(h a))))) f) (λh.(λa.((h(h(h(h a))))) f) y)))))))

L’alligator jaune de gauche ayant un œuf marron devant lui, et 4 œufs jaunes en-dessous de lui, va recolorier en marron ces œufs jaunes :

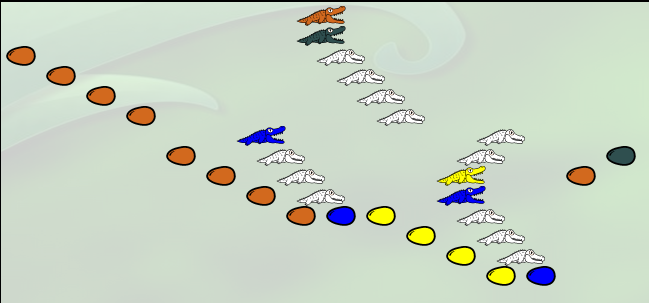
Pour l’instant la λ-expression est devenue

λf.(λy.(f(f(f(f(λa.(f(f(f(f a)))) ((λh.(λa.(h(h(h(h a))))) f) y)))))))

Puis c’est le tour de l’autre alligator jaune :

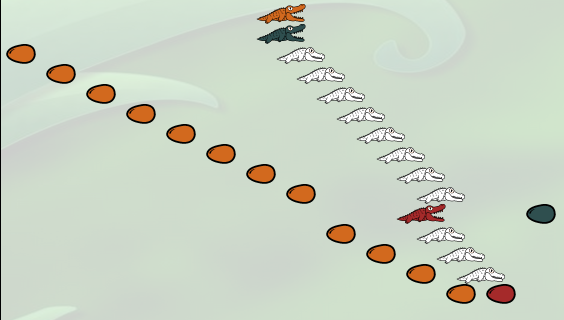
La λ-expression est maintenant devenue

λf.(λy.(f(f(f(f(f(f(f(f(λb.(f(f(f(f b)))) y))))))))))

Il ne reste alors qu’une simplification à faire : Le repas de l’alligator acajou (b) qui va disparaître en mangeant un œuf sapin alors qu’il n’y a pas d’œuf de sa couleur pour prendre le relais. Le résultat représente le nombre 12 puisqu’il y a 12 œufs marron :

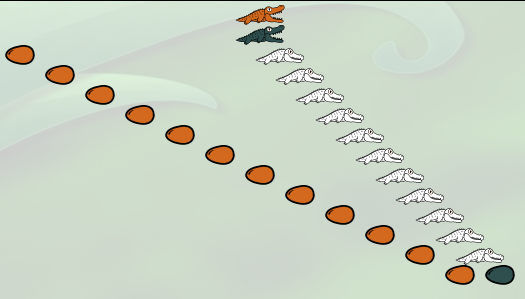
Cela se confirme en comptant les « f » dans la λ-expression obtenue :

λf.(λy.(f(f(f(f(f(f(f(f(f(f(f(f y)))))))))))))

Carrés parfaits

Comme le carré d’un entier a est défini comme le produit de ce nombre par lui-même, on peut définir en λ-calcul la fonction « carré » à l’aide des opérations suivantes :

  • Cliquer sur λa pour définir le nom de la variable dont on va définir le carré ;
  • Cliquer sur « MULT » pour choisir le produit de deux nombres entiers ;
  • entrer a (premier facteur) et encore a (second facteur)

On obtient alors la fonction qui, à a, associe son carré, sous forme d’une λ-expression :

λa. (λm.λn.λf.m (n f)) a  a

Elle se dessine ainsi :

Cette fonction, bien que plutôt simple, peut encore être simplifiée (ou si on préfère, redéfinie). Pour voir ça, il suffit de cliquer sur l’animation jusqu’à ce que la population se stabilise, on a alors la garantie qu’elle ne peut plus se simplifier.

La première étape sera déterminée par l’alligator marron (« m ») qui va absorber le premier œuf bleu, ce qui aura pour effet de le déplacer en bas à gauche :

La première simplification donne ce résultat :

λa.(λn.(λf.(a (n f))) a)

Mais ce n’est pas fini ! Le second œuf bleu est juste devant l’alligator gris qui va donc à son tour le déménager vers le bas :

L’expression une fois simplifiée est

λa.(λf.(a(a f)))

Ah tiens : C’est le nombre 2. Ainsi, on vient de découvrir qu’en λ-calcul, la fonction « carré » est le nombre 2. Qui l’eût cru ? Bien, alors, pour calculer le carré de 5, il suffit de cliquer sur « two » puis « five » et de lancer le λ-calcul sur le résultat obtenu !

Dans le dernier onglet, on va λ-abstraire le procédé pour définir la fonction « puissance » très brièvement en λ-calcul.

revenir aux onglets

Soustraction

La soustraction est beaucoup beaucoup plus compliquée que l’addition, en fait elle est même plus compliquée que la multiplication. C’est le premier mystère du λ-calcul, le second étant qu’au contraire l’exponentiation est nettement plus simple que la multiplication. Cela est dû à ce que la composition des fonctions permet facilement d’ajouter des choses, mais pas d’en enlever (même si des simplifications sont possibles en λ-calcul).

Alors pour soustraire y à x, on peut utiliser une définition récursive du genre

  • si y =0, x-y=x
  • sinon x-y=pred(x)-pred(y)

Il faut donc définir une fonction « prédécesseur ». C’est là que ça devient plus difficile...

On peut définir le prédécesseur à partir du successeur avec cet algorithme (à tester sous alcoffeethmique :

succ = (n) -> n+1
pred = (n) ->
    [dernier,courant] = [0,0]
    until courant is n
        [dernier,courant] = [courant,succ(courant)]
    dernier
affiche pred 2

Pour définir le prédécesseur, on va donc travailler sur des paires du type (n,n+1) (ou (dernier, courant) ci-dessus) et choisir le premier élément de la paire dès que le second est égal à x.

On en arrive donc à devoir définir une nouvelle notion a priori étrangère à l’arithmétique : La notion de paire. Voici, extraite de la console du jeu, une belle paire [2] :

Il faut donc 3 alligators pour faire une paire ! En fait le premier joue le rôle de sélecteur (entre le premier élément de la paire et le second élément de la paire) et les deux autres sont les variables constituant la paire. La λ-expression est

(λx.λy.λz.z x y)

Pour faire une paire (a,b), on place donc cet opérateur suivi de a et de b :

Si maintenant on place devant cette paire l’opérateur

(λp.p (λx.λy.x))

pour obtenir

(λp.p (λx.λy.x))( (λx.λy.λz.z x y) a b)

on a ceci :

Qui évolue jusqu’à la population ne comportant que a : L’opérateur choisit le premier élément d’une paire, il s’appelle donc « first ».

Si maintenant on place devant la belle paire, l’opérateur

(λp.p (λx.λy.y))

qui donne la situation

(λp.p (λx.λy.y))( (λx.λy.λz.z x y) a b)

Celle-là par contre évolue vers l’œuf b seul : L’opérateur choisit donc le second élément de la belle paire, et s’appelle donc « second ».

Ensuite, pour passer de (a,b) à (b,a+1), on applique l’opérateur « second » et l’opérateur « succ » aux deux éléments de la belle paire. Mais on le fait dans une boucle, et il reste à voir comment on boucle dans le λ-calcul, et là encore on a une sacrée surprise : De même que 0 et « faux » sont codés de la même manière,

En λ-calcul, une boucle est réalisée par la fonctionnelle « si...alors...sinon »

Le codage est

(λp.λa.λb.p a b)

Et voici le portrait de l’itérateur en λ-calcul :

Il ne paye pas de mine mais fait des miracles :

  • p est un entier de Church, codant le nombre d’itérations à effectuer
  • a est l’opération à itérer (ici, remplacer (n-1,n) par (n,n+1) comme on l’a vu)
  • b est l’état initial (ici la paire (0,0) qui va évoluer au cours de l’itération).

On constate que si p vaut 0, on peut l’interpréter comme « faux » et l’itérateur n’itère pas, renvoyant b, ce qui est bien ce qu’on attend d’un test « ifthenelse » dans le cas où le booléen est évalué à faux : On a alors le « else ». Par contre si p vaut « vrai », l’itérateur n’itère pas mais renvoie a, ce qui le transforme donc en test. C’est donc la nature de ce qu"on soumet à l’itérateur qui fait de lui un itérateur ou un test.

La fonction « prédécesseur » est effectivement basée sur un itérateur, comme le montre son portrait :

Calculer le prédécesseur de 5 avec les crocodiles est une bonne occasion de voir une boucle tourner.

Finalement, en faisant λm.λa. (a pred) m avec la fonction pred précédente, on obtient le soustracteur en λ-calcul :

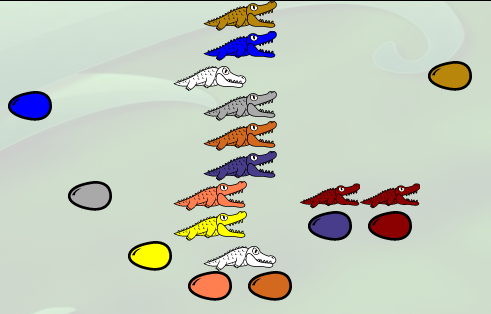
Il consiste à appliquer a fois la fonction « prédécesseur » à m pour soustraire a à m :

soustraction  = (m,a) ->
    m-- for k in [0...a]
    m
affiche soustraction 5, 3

revenir aux onglets

Comparaison

La soustraction vue à l’onglet précédent est définie pour tout couple d’entiers naturels, même si le second entier est plus grand que le premier. Dans ce cas, la soustraction donne 0. Ceci permet de définir un opérateur de comparaison entre entiers naturels :

  • si a est plus petit que b , a-b=0 d’après ce qui précède ;
  • si a est égal à b, là aussi, a-b=0 ;
  • si a est plus grand que b, a-b est strictement positif, en tous cas, non nul.

La relation d’ordre est donc évaluée en comparant à 0 la différence a-b. Ce qui utilise la comparaison à 0, qui est une fonction mixte, puisqu’elle associe un booléen à un entier. Elle est formée de deux familles côte à côte (mais la première ne mange pas la seconde, comme on le verra ci-dessous) :

En fait elle agit en se faisant manger par un numéral, et ce faisant elle provoque une réduction des œufs de cette famille jusqu’à ce qu’il n’en reste plus qu’un, au sein de la moitié gauche de la famille de départ, qui représente le booléen « faux ». Sauf si le numéral est nul, auquel cas la réduction ne peut avoir lieu et renvoie le booléen « vrai » qui est la moitié droite de la famille ci-dessus.

Voyons comment la famille « 3 » digère ce convertisseur booléen :

La famille « 3 » est donc à gauche, et l’alligator du haut s’apprête à manger la famille « faux » qui fait la moitié gauche du prédicat :

Comme il y a 3 œufs de même couleur que lui, ils vont éclore avec pour résultat de créer trois copies de cette famille « faux ». L’essentiel est qu’il y en a au moins une :

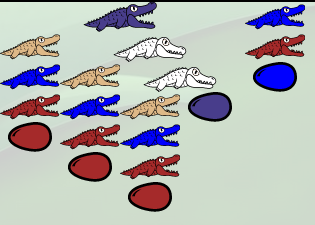
Maintenant l’alligator du haut va absorber la famille « vrai » à droite, ce qui va la déplacer là où est l’œuf bleu foncé. L’important est que cette famille « vrai » sera à portée de gueule d’alligator, sans œuf pouvant éclore pour la reproduire.

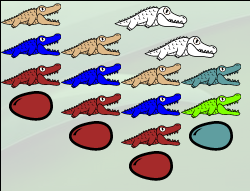
Maintenant c’est l’hécatombe : L’alligator en haut à gauche a presque tout le monde à portée de repas et va dépeupler sévèrement le paysage, d’autant qu’il n’y a pas d’œuf de sa couleur pour reproduire ces éléments. En plus lui aussi va disparaître d’indigestion, ne laissant que la famille « false » qui est en-dessous de lui. Or il se trouve effectivement que « 3=0 » est faux.

Avec n’importe quel autre entier non nul on aurait le même résultat. Voilà maintenant ce qui se passe avec 0 :

Comme il n’y a pas d’œuf de sa couleur, l’alligator en haut à gauche va purement et simplement éradiquer la famille « faux » qui est au milieu :

L’ingestion par l’alligator en haut à gauche produit essentiellement un nettoyage qui ne laisse que la famille « true » survivante. Et effectivement, « 0=0 » est une tautologie.

Voici le test de nullité complet avec ses variables anonymées :

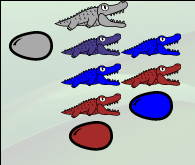
On le revoit dans les trois premières colonnes de la comparaison de deux entiers :

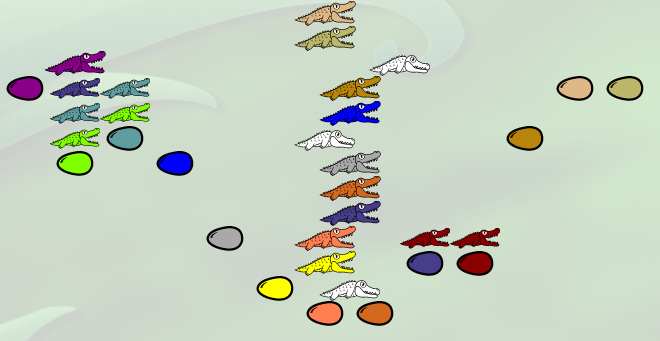
Les deux œufs à droite (protégés par les deux alligators du haut) sont les entiers à comparer. Au milieu, on reconnaît la soustraction. Ce test dit donc bien que a est inférieur à b lorsque a-b est nul.

revenir aux onglets

Puissance

On a vu en bas de l’onglet « multiplication » qu’un nombre étant une fonctionnelle, peut être appliqué à un nombre. Par exemple, en appliquant la fonctionnelle « 2 » au numéral « 3 », on élève celui-ci au carré.

On peut inverser les rôles et appliquer la fonctionnelle « 3 » au numéral « 2 » pour élever 2 au cube. La λ-expression est, au départ,

(λf.λx.(f(f(f x)))) (λg.λy.(g(g y)))

Et lorsque chacun des alligators λf (en marron) et λx (en bleu) absorbe le numéral 2, ils doublent le nombre d’œufs qui sont en-dessous d’œufseux, totalisant ainsi 8 œufs dès la deuxième opération :

 (λf.λx.(f(f(f x)))) (λg.λy.(g(g y)))
 λx.(λg.(λy.(g(g y))) (λg.(λy.(g(g y))) (λg.(λy.(g(g y))) x)))
 λx.(λy.((λa.(λb.(a(a b))) (λa.(λb.(a(a b))) x)) ((λa.(λb.(a(a b))) (λa.(λb.(a(a b))) x)) y)))

Le calcul ne se finit réellement qu’au bout de 18 opérations de simplification (renommage, déplacement et suppression de parenthèses inutiles) pour aboutir au nombre 8.

En fait, si 3 est représenté par la fonctionnelle qui, à g, associe g∘g∘g, en l’appliquant à 2 (fonctionnelle qui, à f, associe f∘f) on a une nouvelle fonctionnelle, qui, à f, associe f∘f∘f∘f∘f∘f∘f∘f, c’est la manière dont fonctionne l’application d’une fonctionnelle à une fonction (ou une fonctionnelle), qui est différente de la composition (c’est le piège). Autrement dit, l’élévation de b (un entier de Church) à la puissance e (pareil) se fait en λ-calcul par e(b) : Difficile d’imaginer plus simple. C’est le second mystère du λ-calcul (le premier étant la complexité de la soustraction) : L’extraordinaire simplicité de l’exponentiation. Pour faire de e(b) une fonctionnelle, on le précède des déclarations de variables b et e, et on a finalement la λ-expression

(λb.λe.e b)

Qui se dessine

(l’exposant en vert, la mantisse en acajou)

On peut donc calculer une puissance en appliquant cet opérateur à deux entiers de Church, par exemple pour calculer le cube de 3, on fait « pow » « three » « three » ce qui donne

(λb.λe.e b) (λf.λx.(f(f(f x)))) (λf.λx.(f(f(f x))))

et produit, au bout d’un temps assez long [3], le numéral 27.

Mais on peut généraliser, en définissant une fonction sur les numéraux, qui, à un entier n, associe nn. On fait « λn », puis « pow » puis « n » et encore « n ». On a alors la définition de la fonction nn :

λn. (λb.λe.e b) n  n

Elle a de l’allure :

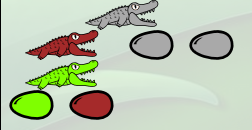
Mais au premier coup d’œil, on constate que l’alligator acajou (λb) a des envies d’omelette avec ces œufs gris devant lui. On peut donc simplifier la fonction « n puissance n » :

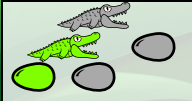
La λ-expression la définissant devient

λn.( λe.(e n ) n )

Mais puisque n est élevé à sa propre puissance, l’exposant est-il réellement nécessaire ? Non puisque l’alligator (vert) se retrouve maintenant face à un œuf gris, ce qui va déménager l’œuf gris en bas à droite et faire disparaître l’alligator vert (indigestion), et tout ce qui était vert va disparaître :

  • l’alligator parce qu’il va mourir d’indigestion
  • l’œuf parce qu’il éclot en donnant naissance à un œuf gris :

La λ-expression définissant n<sup<n est donc tout simplement

λn.( n n )

En fait c’était prévisible, puisqu’on a vu que pour élever un numéral n à sa propre puissance, il suffit de l’appliquer à lui-même et c’est exactement ce que fait cette λ-expression.

Maintenant pour calculer le cube de 3 on peut appliquer cette expression au numéral 3 :

λa.( a a )  (λf.λx.(f(f(f x))))

Le résultat est bien 27 (après moultes simplifications) :

C’est maintenant que ça devient délirant : Puisque nn est une fonctionnelle qu’on n’aplique qu’à une seule fonction, on peut l’appliquer à elle-même (après changement de variable pour mieux comprendre ce qui se passe) :

λa.( a a )  λb.( b b )

Et ce qui se passe quand on essaye de réduire cette expression est ... intéressant :

Il y a des λ-expressions qui, lorsqu’on essaye de les simplifier, deviennent de plus en plus compliquées (surpopulation chez les crocodiles, voir par exemple le combinateur Y), mais celui-là ne converge pas, sans pour autant diverger. Il rappelle un peu le paradoxe du menteur.

La fonction nn est notée ω en λ-calcul et l’expression obtenue en l’appliquant à elle-même est notée Ω=ω ω

revenir aux onglets

Théorie de la subitisation

On définit, en λ-calcul, des fonctions knower qui reconnaissent le cardinal d’un ensemble. On a besoin de fonctions gérant les listes de noms :

  • index calcule la position d’un nom dans le dictionnaire noms ;
  • suivant renvoie le nom suivant un nom donné dans le dictionnaire ;

Mais aussi de fonctions sur les ensembles :

  • estSingleton reconnaît si l’ensemble ne contient qu’un élément (distingue l’unité du pluriel) ;
  • estDoubleton distingue le cas particulier où l’ensemble contient exactement deux éléments ; en effet cette sorte d’ensemble saute aux yeux (subitisation) ;
  • estTripleton distingue une autre catégorie de pluriel avec le nombre 3, reconnu plus vite que les nombres qui lui sont supérieurs.

Essayer le script suivant dans alcoffeethmique, avec des ensembles de diverses tailles, et les différents « knowers » pour voir l’effet obtenu.

noms = ["un","deux","trois","quatre","cinq","six","sept","huit","neuf","dix","onze","douze","treize","quatorze","quinze"]
index = (nom) ->
    (i for i in [0..noms.length-1] when noms[i] is nom)[0]
suivant = (nom) ->
   noms[index(nom)+1]
estSingleton = (ensemble) ->
    ensemble.cardinal() is 1
estDoubleton = (ensemble) ->
    ensemble.cardinal() is 2
estTripleton = (ensemble) ->
    ensemble.cardinal() is 3
# reconnaît l'unité
oneKnower = (S) ->
    if estSingleton(S)
        "un"
    else
        undefined
# reconnaît la dualité
twoKnower = (S) ->
    if estSingleton(S)
        "un"
    else
        if estDoubleton S
            "deux"
        else
            undefined
# reconnaît la trialité
threeKnower = (S) ->
    if estSingleton(S)
        "un"
    else
        if estDoubleton S
            "deux"
        else
            if estTripleton S
                "trois"
            else
                undefined
# reconnaît les nombres par cardinaux
cpKnower = (S) ->
    if estSingleton S
        "un"
    else
       suivant cpKnower (new Ensemble [S.tirerAuSort()]).complémentDans S
affiche cpKnower new Ensemble [1..5]

En rajoutant à la fin les instructions suivantes on constate qu’il faut environ autant de temps pour reconnaître 3 par comptage ou par subitisation :

boucle = -> cpKnower new Ensemble [1,2,3]
subit = -> threeKnower new Ensemble [1,2,3]
affiche chronomètre boucle
affiche chronomètre subit

On a en effet quelque chose comme ceci :

reconnaisance par boucle reconnaissance par subitisation
19 µs 17 µs

Les temps sont très comparables (et même parfois le premier est inférieur au second). Pour comparaison, la reconnaissance de 15 est du même ordre de durée que celle de 3, comme le montre la variante suivante :

boucle = -> cpKnower new Ensemble [1..15]
affiche chronomètre boucle

En fait, même avec un ensemble de taille un milliard, il faut toujours à peu près le même temps donc JavaScript n’est pas adapté pour ce genre de mesure, ou alors il faudrait compter le nombre d’appels récursifs à cpKnower (on peut les afficher dans la boucle). Ainsi, la reconnaissance de 3 par cpKnower fait 3 appels à cpKnower, alors que threeKnower n’est appelé qu’une fois, et prend donc a priori trois fois moins de temps.

Autres constructions

Avec un test de comparaison d’entiers, des paires (d’entiers par exemple), des itérations/tests, on peut aller plus loin. Toutefois la relative lourdeur des résultats donne la préférence à un autre outil, plus concis que les alligators. alcoffeethmique sera choisi ici. D’ailleurs

  • le premier langage de programmation basé sur le λ-calcul est Lisp pour lequel les entiers, et même les réels, sont des « atomes » ;
  • Haskell aussi a des entiers prédéfinis, ce qui améliore la concision et l’efficacité.

Division entière

On peut définir le quotient entier par la propriété archimédienne des entiers. Cela donne ce script (utilisant la comparaison et la soustraction construites plus haut) :

quotient = (n,d) ->
    if n<d then 0
    else 1+quotient n-d, d 
affiche quotient 22, 7

Une fois ce quotient entier défini, le reste euclidien se calcule avec lui et d’autres opérations déjà construites ci-dessus :

quotient = (n,d) ->
    if n<d then 0
    else 1+quotient n-d, d 
reste = (n,d) ->
    n-d*quotient n,d
affiche reste 22, 7

Entiers négatifs

Un entier relatif est une paire d’entiers naturels. On considère comme égaux des entiers comme (5,3) ou (7,5) ou (22,20) ou (2,0) (égaux à 2). Les entiers naturels sont donc des relatifs (a,b) tels que a est supérieur ou égal à b.

On peut définir des fonctions

  • relatif convertissant un entier naturel en sa représentation relative ;
  • opposé calculant l’opposé d’un entier relatif
  • afficher donnant la valeur affichée d’un entier :
    • si cet entier est naturel, soustraire le second élément du premier
    • sinon faire la soustraction inverse et précéder d’un signe « moins »
relatif = (n) ->
    [n,0]
opposé = (z) ->
    [z[1],z[0]]
afficher = (z) ->
    affiche z[0]-z[1]
afficher opposé relatif 3

Un test pour savoir si un entier est naturel peut aussi être déduit des constructions précédentes :

estNaturel = (z) -> 
    z[0] >= z[1]
affiche estNaturel relatif 3

Définition de l’addition des relatifs :

relatif = (n) ->
    [n,0]
opposé = (z) ->
    [z[1],z[0]]
afficher = (z) ->
    affiche z[0]-z[1]

somme = (z1,z2) ->
    [z1[0]+z2[0],z1[1]+z2[1]]

a = relatif 5
b = opposé relatif 3
afficher somme a, b

Définition de la soustraction :

relatif = (n) ->
    [n,0]
opposé = (z) ->
    [z[1],z[0]]
afficher = (z) ->
    affiche z[0]-z[1]

différence = (z1,z2) ->
    [z1[0]+z2[1],z1[1]+z2[0]]

a = relatif 5
b = opposé relatif 3
afficher différence a, b

Définition de la multiplication :

relatif = (n) ->
    [n,0]
opposé = (z) ->
    [z[1],z[0]]
afficher = (z) ->
    affiche z[0]-z[1]

produit = (z1,z2) ->
    [z1[0]*z2[0]+z1[1]*z2[1],z1[1]*z2[0]+z1[0]*z2[1]]

a = relatif 5
b = opposé relatif 3
afficher produit a, b

La division peut être implémentée avec des tests sur les signes respectifs du numérateur et du dénominateur, et la règle des signes accompagnée de la division entière construite dans l’onglet précédent.

quotientNaturels = (a,b) ->
     troncature a/b
abs = (z) ->
    if z>=0 then z
    else -z
signeproduit = (a,b) -> a*b>=0
quotientRelatifs = (n,d) ->
    q=quotientNaturels abs(n), abs(d)
    if signeproduit n,d then q
    else -q
affiche quotientRelatifs -22,-7

Fractions et autres

Une fraction aussi peut être représentée par une paire d’entiers. Pour la simplifier on a besoin du pgcd qui se calcule par l’algorithme d’Euclide avec des tests et boucles déjà construits. Voici un exemple fait en classe. Avec alcoffeethmique on peut regarder le code source :

  • créer une fraction a
  • afficher a
  • afficher la liste de tous les x de a (ce qu’on peut faire avec x for x of a) ; constater qu’il y a « plus » dedans ;
  • afficher a.plus pour voir comment les fractions sont additionnées :
a = new Fraction 3,2
affiche a
affiche (x for x of a)
affiche a.plus

Les réels ne peuvent être représentés en machine donc on se contente de fractions. Les complexes peuvent aussi être représentés comme paires de fractions par exemple, avec les opérations sur paires. Noter que les complexes aussi sont dans alcoffeethmique, et on peut les explorer avec ce genre de script :

z = new Complexe 2,-1
affiche z
affiche z.fois


[1] à ne pas confondre avec λf.f qui est l’identité

[2] D’après Philippe Bouvard, elle proviendrait de Loches...

[3] Le navigateur Chrome est vivement recommandé pour ce genre d’expérience risquée...


Commentaires

Logo de eti
jeudi 29 avril 2021 à 12h45 - par  eti

Bonjour, même si je n’ai pas cherché à comprendre les crocodiles, j’ai enfin compris la représentation des nb entiers et du successeur. Bravo, malgré plusieurs cours, pdf et page web, c’est la première fois que c’est clair en terme de signification et de calcul. Merci