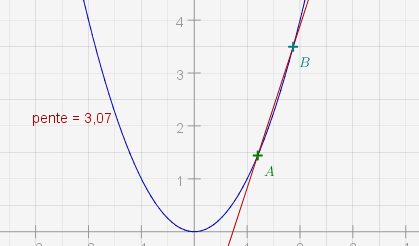
La manière classique utilisée pour « montrer » un nombre dérivé est l’utilisation sous un logiciel de géométrie dynamique, de ce genre de construction, où lorsqu’on approche B de A, on constate une convergence du coefficient directeur vers une valeur limite que l’on définit ensuite comme étant f’(a) :
Ensuite le programme recommande, non de supplanter, mais de supplémenter, cette manipulation par une activité algorithmique. L’algorithme est de ce genre :
h prend 0,001
entrer a, b et leurs images
tant que b>a faire
enlever h à b;
recalculer f(b);
recalculer la pente;
fin tant que
afficher la penteMais au début ça va trop lentement (b est trop éloigné de a) et à la fin ça va trop vite (plus b est proche de a, plus h est important par rapport à b-a). Pour améliorer l’algorithme, on peut faire parcourir les puissances de 10 (ou autre nombre positif) par h (par exemple 0,1 puis 0,01 puis 0,001 etc.). Bref, au lieu que b-a suive une progression arithmétique de précision constante, on peut lui faire suivre une progression géométrique de précision croissante.
Or les langages tels c++, Java, JavaScript ou Xcas ont une syntaxe de boucle complexe mais puissante (c’est le cas de le dire !) qui facilite nettement le calcul de progressions géométriques. Par exemple, pour calculer les puissances de 2 inférieures à un million en JavaScript, il suffit d’entrer
for(p=1;p<=1000000;p=2*p){...}Pour voir ce que cela donne dans l’exemple présent, il suffit de consulter le CaRScript de la figure ci-dessus (en cliquant sur « modifier » dans le menu qui apparaît quand on sélectionne le script, avec l’icône représentant un script).
Ce TP bicéphale est donc parfaitement réalisable avec un outil tel Xcas ou CaRMetal qui permet de faire la partie géométrie dynamique (du début) et la partie programmation sans avoir à démarrer un autre logiciel.
Ci-dessous, un exemple de TP basé sur cette méthode :

Commentaires