En effet, si on peut considérer les tables de logarithmes comme moyen de faciliter le calcul de produits, c’est que l’effort d’effectuer les produits a été fait préalablement par les concepteurs de tables. La question de savoir comment ils ont fourni cet effort se pose alors assez naturellement...
Avant Neper
Un algorithme de multiplication par tables peut être étudié dès le collège (faire la table est facile avec un tableur). Il remonterait au moins aux Babyloniens [1]. Le principe est simple : si on développe (x+y)2-(x-y)2, on trouve 4xy, donc avec une table de la fonction x2/4, on a juste une addition (x+y), une soustraction (x-y), deux lectures de tables et une soustraction à effectuer. Par exemple, pour multiplier 0,8 par 0,7, on les additionne et les soustrait respectivement, obtenant ainsi 1,5 et 0,1, dont on lit les images dans la table :
Ensuite, il suffit de soustraire 0,0025 à 0,5625 pour avoir le produit 0,56.
Au temps où les ordinateurs mettaient nettement plus de temps à effectuer des multiplications que des additions, cet algorithme permettait de rapidement effectuer des multiplications sans occuper trop de mémoire, la table des carrés des entiers allant de 0 à 20 occupant 21 emplacements mémoire, alors que la table de Pythagore au complet (pour les deux facteurs allant de 0 à 10 en occupe 121 ce qui est nettement plus.
Henry Briggs était féru d’astronomie, et avait déjà, comme la plupart de ses contemporains, l’habitude d’effectuer des multiplications à l’aide de tables trigonométriques, avec l’algorithme dit « de la prosthaphérèse ». Par exemple, voici comment on peut effectuer 0,8×0,7 avec une table de cosinus à 30 minutes près (elle aussi, gracieusement fournie en bas de l’article) :
- On cherche de quel angle 0,8 est le cosinus :
- On cherche de quel angle 0,7 est le cosinus :
- On additionne ces angles (37°+45°30’=82°30’), et on les soustrait (45°30’-37°=8°30’) ;
- On cherche enfin les cosinus de la somme
et de la différence :
- On additionne les deux cosinus obtenus, et on divise le résultat par 2 : 0,13053+0,98902=1,11955 et 1,11955÷2=0,559775 ; ce qui permet de dire que 8×7 font environ 55,9775 : Pas mal en termes de précision !
Algorithme
La technique utilisée par John Neper pour calculer ses logarithmes consistait essentiellement à mettre côte à côte deux suites, l’une arithmétique, l’autre géométrique (de raison très proche de 1) et de les ajuster l’une à l’autre. L’algorithme de Neper, proche de celui exposé ci-dessous, permet de calculer toute une table d’un coup.
Henry Briggs, ayant passé pas mal de temps à effectuer des multiplications avec ses propres tables de trigonométrie, était à même d’apprécier l’utilité des tables de logarithmes de Neper, et fit tout ce qu’il put pour rencontrer ce dernier, avec qui il a collaboré à l’édition de la première table de logarithmes décimaux, en utilisant un algorithme permettant de calculer un seul logarithme à la fois (au besoin), et que voici :
Algorithme de Briggs
Entrée : Un réel x strictement positif
Variable : Un entier n
- Tant que x est éloigné de 1 (à 0,001 près par exemple), faire
- incrémenter le compteur n ;
- remplacer x par sa racine carrée
- Comme le logarithme népérien d’un nombre x proche de 1 est proche de x-1, on prend x-1 comme valeur approchée du logarithme ; n vaut alors le nombre de fois qu’on doit doubler x-1 pour avoir le logarithme du nombre de départ.
- Faire n fois :
- Multiplier le logarithme par 2
Sortie : Le nombre obtenu est le logarithme népérien de x.
Cet algorithme est donc très intéressant parce qu’il synthétise à peu près tout le programme du lycée : Test de positivité (à moins qu’on soit prêt à prendre le risque de calculer la racine carrée d’un nombre négatif), boucle à nombre prédéterminé d’itérations (la deuxième boucle, puisque n est connu) et boucle à condition de sortie (la première boucle, dont le but est essentiellement de calculer le nombre n). Par contre, cet algorithme n’est pas classique parce que, contrairement aux habitudes du lycée, on n’entre pas de valeur de x dont on veut calculer le logarithme, mais on définit algorithmiquement une fonction dont on cherche essentiellement à voir si sa représentation graphique est proche de celle du logarithme de la machine. Sur l’aspect fonctionnel des algorithmes, voir cette discussion. Pour rapidement tester l’algorithme en représentant graphiquement la fonction ainsi définie,
CaRMetal
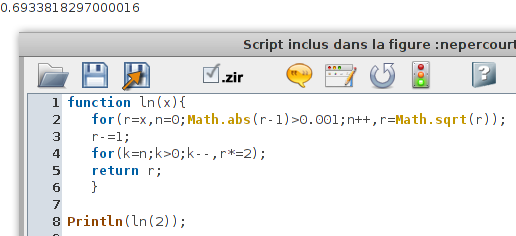
L’algorithme se traduit assez aisément en JavaScript [2] :
Ensuite il suffit de lancer le programme (en cliquant sur le feu vert) après y avoir ajouté des instructions comme
Println(ln(2));ou
a=ln(2);
b=Math.log(2);
Println((a-b)/b*100);Mais comme on a défini une fonction, autant la représenter graphiquement, en ajoutant à la figure un point pilote appelé Px sur l’axe des abscisses, et un point M dont la trace est active, et dont les coordonnées sont fixées par le script :
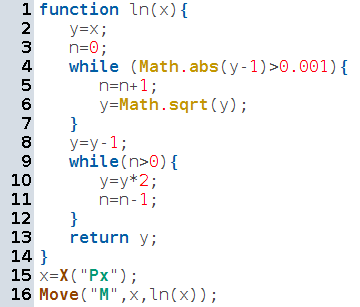
Ensuite, pour éviter d’avoir à relancer trop souvent le script, il suffit d’automatiser son lancement avec le gestionnaire de scripts, de telle manière que chaque mouvement de Px relance le script :
Le tracé de la représentation graphique de la fonction (en rouge) est remarquablement proche de celui (en vert) de la représentation graphique du logarithme népérien :
L’énoncé du TP est téléchargeable en bas de l’article (au format pdf). On remarquera comment l’usage de LaTeX a permis d’évoquer une suite récurrente sans vraiment en parler.
Le TP dure une heure en ne comptant pas le III (seuls 2 élèves ont réussi la représentation graphique au bout de l’heure) et une heure et demie si on veut que tout le monde finisse. Il vaut donc mieux donner le I et le tableau du II en devoir maison avant le TP, et laisser les élèves passer du temps sur le III (recopier le JavaScript est très rapide) ; le II/3) prend pas mal de temps...
Les élèves ne recopient presque jamais les points-virgules, sans doute parce qu’ils ne les voient pas !
Deux élèves ayant, par mégarde, ajouté un zéro à 0.0001, on eu un logarithme plus précis ; ce qui a été intéressant à discuter en classe pendant le TP. L’erreur d’approximation sur le logarithme de 2 est environ trente fois le seuil de la première boucle.
Xcas
Avec Xcas, l’écriture de l’algorithme coïncide avec la définition d’une fonction appelée Neper :
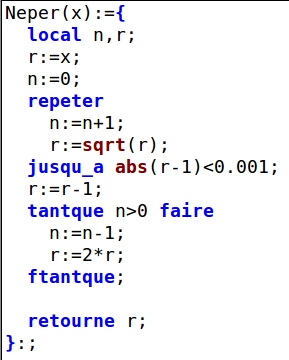
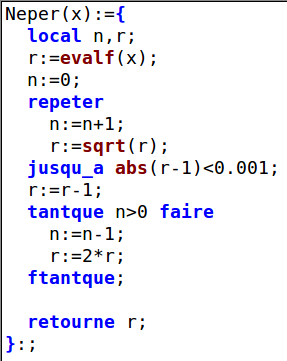
Ensuite pour calculer une valeur approchée de ln(2) il suffit d’entrer Neper(2) et d’appuyer sur « entrée » pour voir le résultat. Mais le logarithme d’un nombre entier est alors donné sous forme exacte, alors il faut préciser que c’est à une valeur approchée qu’on s’intéresse :
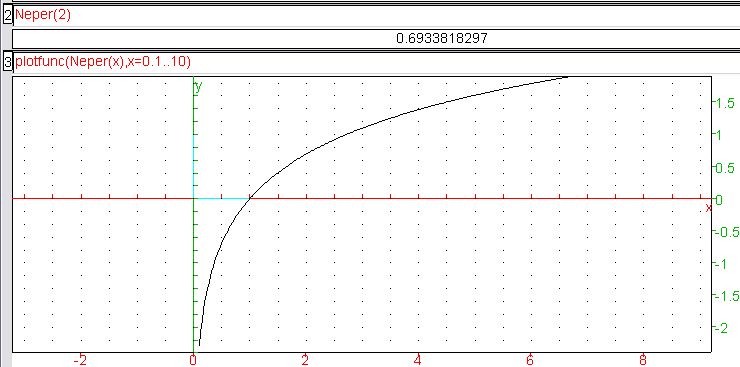
Maintenant que la fonction est définie, Xcas peut la représenter graphiquement :
Par contre, vouloir calculer la dérivée est un peu exagéré...
tableur
Comme le tableur « Calc » de Libre Office ne possède pas de fonction appelée Neper, on peut définir celle-ci en Basic. Pour cela, on clique sur « Gestion des outils » et là, on choisit (parmi 4 langages de programmation !) le langage « Basic Libre Office ». Puis on traduit en Basic, avec une belle coloration syntaxique, l’algorithme de Briggs :
Après ça, on peut utiliser cette nouvelle fonction dans le tableur, en écrivant des formules telles que =Neper(2) pour calculer des logarithmes de façon non conventionnelle...
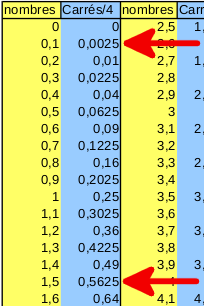
Par exemple, pour faire une table de logarithmes « à la Neper », on peut mettre le nombre 0,1 dans la cellule A2, le nombre 0,2 dans la cellule A3, sélectionner ensemble les deux cellules et copier vers le bas jusqu’à 2 par exemple, puis dans la cellule B2, écrire la formule =Neper(A2) qu’il suffit de copier vers le bas pour avoir une table de logarithmes !
Ensuite, dans la cellule C2, on peut écrire une formule comme =Ln(A2) puis la copier vers le bas pour comparer les deux logarithmes népériens ; et, en mettant en D2 la formule =(C2-D2)/D2, on peut afficher les erreurs d’approximation, qui sont assez faibles :
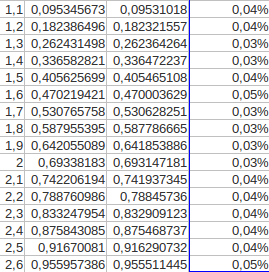
mais également assez fluctuantes :
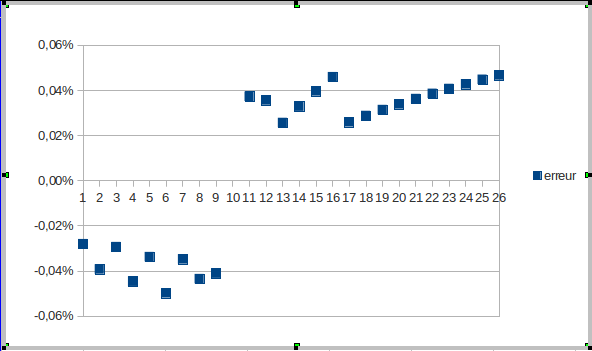
Scilab
Scilab aussi sait représenter graphiquement une fonction définie algorithmiquement ; l’algorithme est plutôt court à rédiger :
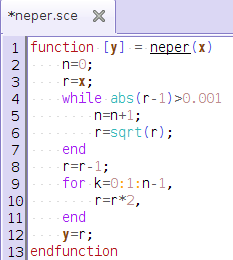
Surprise (voir onglet suivant) : Même avec un nombre négatif, l’algorithme converge :
Pour représenter graphiquement la fonction il faut utiliser fplot2d (et non plot2d) :
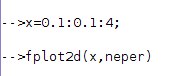
Le résultat est presque immédiat :
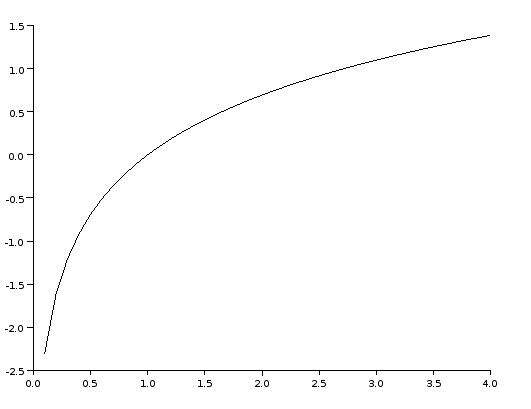
Et Scilab peut exporter la figure à un format vectoriel comme eps ou pdf qui permet d’obtenir un rapport de TP très professionnel...
Prolongements
Question troublante : À quel moment exactement, a-t-on utilisé le fait que x est positif ?
Réponse : Jamais ! En fait, si x=0, la suite un+1=√(un) ne tend pas vers 1 ; dans tous les autres cas (y compris si x est négatif !) la suite converge vers 1, et donc l’algorithme converge aussi : L’algorithme de Briggs-Neper permet de calculer le logarithme de tout complexe non nul, et pas seulement des réels positifs. Vérification expérimentale avec Ruby :
Tout d’abord le calcul de ln(2) avec Briggs :
Ensuite, pour s’amuser, on remplace juste 2 par -2 :
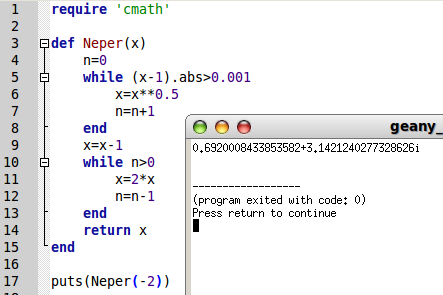
Surprise : L’algorithme calcule un nombre qui peut être appelé logarithme de -2 ! Et d’ailleurs le module de nombres complexes de Ruby est doté d’un (autre) algorithme de calcul de logarithmes de nombres complexes :
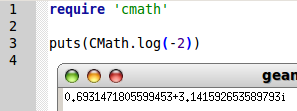
On peut assez facilement vérifier de façon formelle que ce nombre est ln(2)+πi : En effet l’exponentielle de ce nombre est eln(2)eiπ=2×(-1)=-2 cqfd !
Ce TP expliquant comment Briggs calculait des logarithmes à partir de racines carrées, est idéalement complété par un TP expliquant ... comment calculer des racines carrées ; l’algorithme de Heron convient...
Commentaires