Voici des exemples de nuages de points obtenus à l’aide de la fonction Math.random() de JavaScript. Chaque nuage tourne automatiquement dans une page html qui lui est consacrée, et qu’on peut ouvrir en cliquant sur la copie d’écran. Si la page paraît vide, c’est
- qu’on utilise un navigateur ne reconnaissant webGL (par exemple, webGL n’y est pas installé) ; ou
- qu’on utilise un ordinateur non doté de processeur graphique.
Noter que ces nuages de points, sous le nom de « système de particules », sont très utilisés dans l’industrie cinématographique, notamment
- pour synthétiser des météores comme les nuages ou le brouillard
- pour synthétiser des champs d’astéroïdes en SF
- pour synthétiser des nébuleuses, des galaxies, des flammes (le seigneur des anneaux, le dragon crache des nuages de points rouges) et de la fumée
- pour synthétiser (en dessinant leur trajectoire) des brins d’herbe
- pour ajouter un système pileux aux créatures synthétiques (les cheveux des minimoys par exemple, sont des trajectoires d’un nuage de points)
- pour représenter des foules immenses (le seigneur des anneaux, la bataille finale) ou des bancs de poissons (Nemo)
- etc
cube
On a vu que lorsque ses coordonnées sont des variables aléatoires uniformes sur [0,1], la loi suivie par un point est uniforme aussi, mais sur le carré [0,1]². Ce résultat se généralise à l’espace, où le point (x,y,z) suit une loi uniforme dans un cube si x, y et z sont uniformes de même loi et indépendantes.
En dessinant 10000 points suivant une loi uniforme sur [-1,1]3, on voit un cube translucide (mais surtout, rempli !) :
Le fait que la loi est uniforme dans le cube signifie que, si un volume V est inclus dans le cube, la probabilité que (x,y,z)∈V est le quotient du volume de V par celui du cube. Par exemple, si V est la boule unité, son volume valant 4π/3 et celui du cube, 8, la probabilité qu’un des 10000 points ci-dessus soit dans la boule est π/6. Ce résultat est à la base d’une estimation de π par la méthode de Monte-Carlo tridimensionnelle.
On peut aussi remplir le cube par une loi non uniforme, par exemple le produit de probabilités suivant la loi de Xenakis :
La loi de Xenakis étant une loi bêta de paramètres 1 et 2, peut être simulée comme minimum de deux variables aléatoires uniformes (ce qui est fait ici). Alors le minimum de x, y et z suit une loi bêta de paramètres 1 et 6 (puisque c’est la loi du minimum de 6 variables aléatoires uniformes). Mais cela ne donne pas la loi de (x,y,z) lui-même. On conjecture juste que ses lignes de niveaux ressemblent à des triangles.
cylindre
De façon similaire, on peut espérer remplir uniformément un cylindre avec trois variables aléatoires :
- r, uniforme sur [0,1] ;
- t, uniforme sur [0,2π]
- z, uniforme sur [-1,1].
Les coordonnées r,t et z sont celles d’un point aléatoire en coordonnées cylindriques. Mais on voit bien que le point aléatoire en question n’est pas uniformément distribué dans le cylindre, les points étant plus denses près de l’axe de celui-ci :
En fait, il s’agit du phénomène vu ici : Sans tenir compte de z, le point de coordonnées circulaires r et t ne suit pas la loi uniforme dans le disque. Pour avoir une répartition uniforme dans le disque, on sait qu’il faut prendre pour r, la racine carrée d’une variable aléatoire uniforme. Ce qui remplit bien le cylindre uniformément :
nuages gaussiens
Le procédé pour construire un point gaussien a été vu ici : En prenant x et y normaux, centrés, réduits et indépendants, le couple (x,y) suit une loi normale en dimension 2. Le procédé se généralise à la dimension 3 [1].
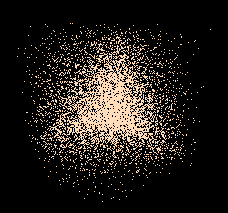
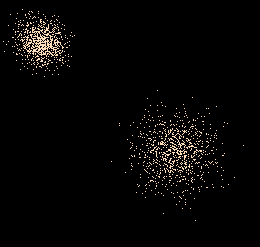
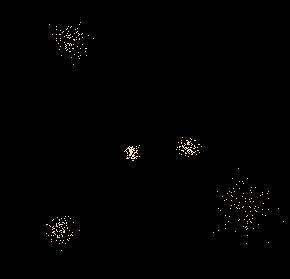
Voici un exemple, avec deux points gaussiens d’écarts-type différents :
Le point en haut à gauche est le plus proche ; s’il paraît plus petit c’est parce qu’il a un écart-type plus petit [2].
On a vu ici que, si les sommets d’un triangle sont gaussiens, le centre de gravité du triangle aléatoire ainsi formé est lui aussi gaussien, dont l’espérance est l’isobarycentre des espérances [3], et dont l’écart-type est √(3) fois plus petit que celui des sommets du triangle. Le fichier ci-dessous montre qu’il en est de même pour un tétraèdre aléatoire, dont les sommets sont gaussiens :
Les 4 sommets ont même écart-type, mais celui qui est le plus éloigné (à droite) a l’air plus grand que le centre de gravité (à sa gauche), ce qui montre bien que l’écart-type de celui-ci est plus petit que l’écart-type des sommets. Ce résultat est à la base de la statistique inférentielle, où, pour avoir une estimation précise d’une grandeur, on effectue la moyenne de ses mesures sur un grand échantillon.
sphère
Le problème vu dans l’onglet sur les cylindres se retrouve aussi en prenant des coordonnées sphériques uniformes : Certaines zones sont plus remplies que d’autres. On va alors séparer le problème en deux parties. Ici on cherche comment obtenir une loi uniforme sur une sphère, et dans l’onglet suivant on s’occupera du rayon.
Comme coordonnées sphériques, on fera ici un choix non conventionnel :
- x = cos(u) cos(v)
- y = cos(u) sin(v)
- z = sin(u)
avec u et v uniformes sur [0,2π]. On voit bien que la probabilité obtenue n’est pas uniforme sur la sphère :
Le pôle nord (en haut à droite) et le pôle sud (en bas à gauche) sont plus visités que le reste de la sphère.
Deux remèdes fonctionnent bien ; le premier, non choisi ici, consiste à prendre un (x,y,z) gaussien centré réduit, et de la normaliser [4]. Par construction, on a une mesure de probabilité invariante par les rotations de l’espace, ce qui est ce qu’on voulait. Le second remède est analogue à ce qu’on a fait pour le cylindre (et qu’on fera pour la boule unité dans l’onglet suivant) : On remplace u par une variable aléatoire dont le sinus est uniforme sur [0,1]. Et la sphère est uniformément visitée :
Maintenant, que se passe-t-il si on multiplie un tel vecteur de norme 1 uniformément distribué sur la sphère, par un rayon uniformément distribué sur [0,1[? Voir l’onglet suivant...
boule
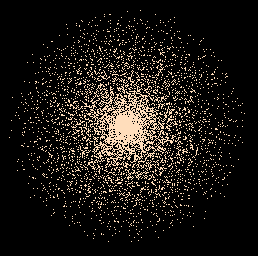
Comme un point uniformément distribué sur la sphère est statistiquement invariant par toute rotation autour de (0,0,0), il en est de même pour son produit par une variable aléatoire uniforme sur [0,1[. En plus, par construction, le résultat est dans la boule unité. Mais visiblement pas uniformément distribué dans la boule :
Dans le fichier ci-dessus, la caméra a été placée à l’intérieur de la boule pour qu’on voie mieux le cœur dense de cette boule non uniforme.
Pour en savoir plus, on peut utiliser la fonction de répartition de la distance à l’origine, pour une variable uniforme dans la boule. Pour une telle variable, la probabilité qu’elle soit inférieure à R est le quotient du volume de la boule de rayon R (4/3πR3) par celui de la boule de rayon 1 (4/3π). Ce quotient est le cube de R, on veut donc que la variable aléatoire r ait un cube uniforme sur [0 ;1[, et on prend la racine cubique d’une variable uniforme ; cela donne une boule uniformément remplie :
On peut aller plus loin, en prenant la racine sixième d’une variable aléatoire uniforme. La boule est alors creuse, comme on le voit avec un traveling avant de la caméra qui traverse successivement deux couches de points proches de la sphère :
fractals
On finit ici par des nuages de points dont la dimension fractale est inférieure à 3 : Ce sont moins que des volumes, bien qu’ils soient en 3D. On peut aussi voir ceci pour un autre exemple que ceux traités ici.
Le triangle de Sierpinski est connu, et la facilité à le dessiner par système de fonctions itérées : On remplace, à chaque étape, le point M par son milieu avec A, B, ou C au hasard. Le principe se généralise aisément à un tétraèdre ABCD :
La version anaglyphe pour ceux qui ont des lunettes rouge/cyan.
Le même algorithme permet de dessiner un octaèdre fractal :
Sa dimension fractale est ln(6)/ln(2) ≈ 2,585
Une variante (le tiers au lieu de la moitié) permet de dessiner un ensemble de Cantor en 3D :
En vue de dessus, il a l’air connexe (fractale de Vicsek) mais il ne l’est pas du tout...
Un autre ensemble de Cantor basé sur un cube :
Statistiques en 3D
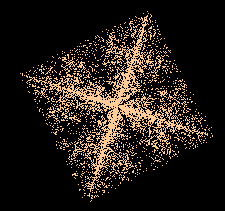
Pour faire des nuages de points en 3D (par exemple pour chercher des corrélations), on a besoin de données. Un bon moyen d’en obtenir est de les simuler. Par exemple, une marche aléatoire en 3D :
Mais on peut aussi dessiner des nuages de points obtenus par des relevés de données réelles. Par exemple, les durées des éruptions du geyser « Old Faithful », téléchargeables ici. Le problème est qu’on ne veut que les données de la deuxième colonne : Voici un extrait du fichier :
1 3.600 79
2 1.800 54
3 3.333 74
4 2.283 62
5 4.533 85
6 2.883 55La première colonne indique le numéro de l’éruption, qui a peu d’intérêt ici. La troisième colonne indique la durée d’attente avant le début de l’éruption. On ne voudrait que les données de la seconde colonne. Pour cela on enlève le début du fichier pour ne garder que les nombres (les trois colonnes) et on enregistre le tout dans un fichier faitful.txt téléchargeable ci-dessous. Puis on transforme ce fichier avec awk. En écrivant
awk '{print $2}' faithful.txt
On a l’affichage de la deuxième colonne seule, mais
- les résultats sont à la ligne (on les préférerait séparés par une virgule)
- le résultat est juste affiché (pas stocké dans un fichier)
La sortie ressemble pour l’instant à ceci :
4.117
2.150
4.417
1.817
4.467 awk permet de rajouter la virgule :
awk '{print $2, ","}' faithful.txt
produit
4.117 ,
2.150 ,
4.417 ,
1.817 ,
4.467 , Reste à se débarasser des passages à la ligne. Bien que awk connaisse les expressions régulières, on peut brancher la sortie de ce que awk a produit sur l’entrée du traducteur tr (Unix) qui va remplacer chaque passage à la ligne (’\n’ comme « newligne ») par une virgule (’,’). C’est du travail à la chaîne (de caractères)... Le branchement se fait par un tuyau « pipe », qui est symbolisé par le caractère « | » [5].
En exécutant
awk '{print $2}' faithful.txt | tr '\n' ','
la fin ressemble maintenant à
4.750,4.117,2.150,4.417,1.817,4.467,
Il ne reste alors plus qu’à enlever la dernière virgule, ce qui peut se faire manuellement dans le fichier eruptions.txt dans lequel on va maintenant enregistrer cette liste de données. Ceci en redirigeant le flux de sortie vers ledit fichier, à l’aide du caractère « > » qui suggère une flèche allant vers le fichier :
awk '{print $2}' faithful.txt | tr '\n' ',' > eruptions.txt
Après l’exécution de ce script, le fichier eruptions.txt contient ceci :
Pour trouver le bon zoom en 3D, on a besoin du maximum des durées d’éruption. Pour cela on initialise une variable max et on la remplace successivement par les durées d’éruption qui sont plus grandes qu’elles. Noter qu’ensuite (après END) on exécute un autre programme en awk qui ne fait que l’affichage :
awk '{if(max==""){max=$2};if(max<$2){max=$2}} END {print max}' faithful.txt
On apprend alors que la durée maximale est 5.1. Dans le fichier ci-dessous on a donc placé la caméra à 16 unités pour être certain de voir tout le nuage :
Un phénomène mystérieux apparaît alors : Les points du nuage ne semblent pas répartis tout-à-fait au hasard mais proches des sommets d’un cube (le cube magique de Yellowstone ?). En fait cela n’a rien de mystérieux lorsqu’on regarde l’histogramme [6] de la série statistique :
L’histogramme montre que la série statistique est bimodale et que les durées d’éruption sont proches soit de 1,8 soit de 4,6. Il est donc parfaitement prévisible que les points soient proches des sommets d’un cube. Les coordonnées étant
- (1,8 ;1,8 ;1,8)
- (1,8 ;1,8 ;4,6)
- (1,8 ;4,6 ;1,8)
- (1,8 ;4,6 ;4 ;6)
- (4,6 ;1,8 ;1,8)
- (4,6 ;1,8 ;4,6)
- (4,6 ;4,6 ;1,8)
- (4,6 ;4,6 ;4 ;6)
Cet example est intéressant en statistique, notamment dans l’optique de tracer plusieurs nuages de points.
Logique floue
Patrick Grim a trouvé un moyen de résoudre le paradoxe d’Épiménide :
| « La présente phrase est fausse » |
Le paradoxe vient de ce qui si la phrase est vraie, alors ce qu’elle affirme l’est, et du coup elle est fausse. Mais alors ce qu’elle affirme est faux aussi et il est faux qu’elle est fausse : Elle redevient vraie. Autrement dit, si on représente la valeur de vérité de cette phrase par x∈{0,1} alors en réflechissant à la phrase (en faisant des hypothèses sur x), comme la valeur de vérité de la négation de la phrase est 1-x, on est amené à remplacer x par 1-x répétitivement ce qui amène à une oscillation (entre x=0 et x=1). La suite n’étant pas convergente, on ne sait pas si on doit considérer que x=0 ou que x=1.
Mais la logique floue permet de résoudre le paradoxe en admettant que la phrase d’Épiménide est à moitité vraie. Alors elle est aussi à moitité fausse et il n’y a plus de paradoxe : La phrase d’Épiménide n’est même pas à moitié paradoxale !
Patrick Grim enseigne au département de philosophie de l’université de New-York. Dans son livre il a visiblement choisi les opérations de logique floue qui lui permettaient d’atteindre le chaos sur ordinateur :
- le minimum pour la conjonction (à gauche dans cet article)
- le maximum pour la disjonction (à gauche aussi)
- mais l’implication de Łukasiewicz (à droite dans l’article de Grim)
- Ce qui aboutit à prendre 1-|x-y| comme valeur de vérité de l’équivalence logique.
- Et pour traiter de modalité, l’adverbe « très » est traduit par Grim, en élévation au carré de la valeur de vérité.
Ceci est rappelé dans un article de Ian Stewart (mathématicien) qu’on peut lire ici ou là. Grim et Mar découvrent la notion de « menteur chaotique » avec la version à deux phrases du paradoxe :
| La phrase suivante est vraie |
| La phrase précédente est fausse |
En réinterprétant les phrases X et Y par de la logique floue, Grim et Mar proposent alors
- X et Y sont équivalentes (ce qui amène à remplacer x par 1-|x-y|)
- Y et ¬X sont équivalentes, ce qui amène à remplacer y par 1-|x+y-1|.
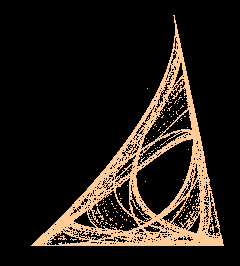
Alors ce système dynamique est chaotique, d’attracteur triangulaire (les coordonnées des sommets sont (1,0), (0,1) et (1,1) : La moitié du carré unité sur lequel sont définis x et y).
Voici alors un système dynamique à trois variables :
| X : Les valeurs de vérité des propositions Y et Z ne sont pas très différentes |
| Y : X est aussi vraie que Z est fausse |
| Z : X et Y sont équivalents |
Le système dynamique consiste donc à remplacer simultanément
- x par 1-(y-z)²
- y par 2-(x+z)
- z par 1-|y-x|
Alors on constate une très lente convergence vers (1,1/2,1/2) :
On conclut la résolution de ce « paradoxe » par le fait que Y et Z sont à moitié vraies et que du coup, X est vraie quant à elle (1/2 n’est effectivement pas très différent de 1/2...)
Une légère variante sur Z aboutit à un attracteur étrange fractal mais plan :
| X : Les valeurs de vérité des propositions Y et Z ne sont pas très différentes |
| Y : X est aussi vraie que Z est fausse |
| Z : Les valeurs de vérité des propositions Y et X ne sont pas très différentes |
Donc au lieu de remplacer z par 1-|y-x| on le remplace par 1-(y-x)² ce qui donne un attracteur étrange :
Voir ici pour en savoir plus sur la logique dynamique.


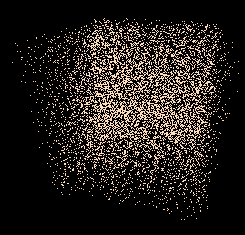

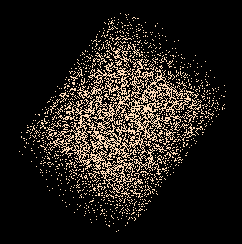




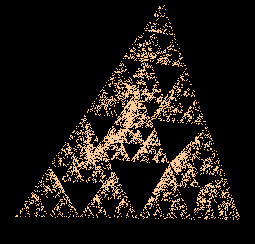
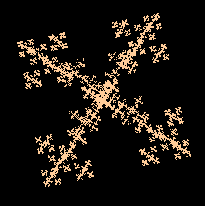


Commentaires