Inde
Le calendrier a fait qu’une fois de plus, Pondichery a été l’académie pionnière. Ce sont les élèves de ce collège qui ont découvert à quoi peut ressembler un sujet sur Scratch par écrit. Les élèves des deux classes de 3e de Pondichery, n’ayant pas trop souffert de problèmes d’équipement, et malgré la disparition d’une demi-heure, ont été régulièrement entraînés à Scratch durant tout le tiers de cycle 2016-2017, et ne semblent pas avoir été trop déroutés par le sujet : Leurs enseignants ont anticipé sur l’utilisation algébrique de Scratch.
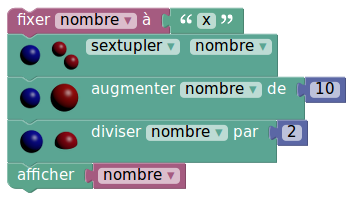
Voici, à fin de comparaison, les versions Sofus et Scratch du programme de calcul de Julie :
| Sofus | Scratch |
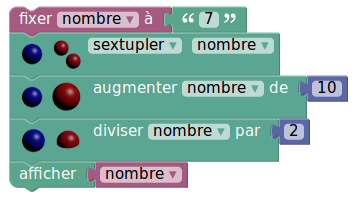
|

|
En résumé, ce sujet, s’il est intéressant per se, pose la question de la pertinence de Scratch pour des activités numériques, du moins sur des programmes de calcul. Il pose aussi la question du mode d’évaluation, un sujet écrit n’étant pas nécessairement pertinent sur un logiciel fait pour manipuler en ligne.
USA
Le sujet de Washington met la barre haut : Deux exercices portant sur des programmes !
Exercice 5
L’exercice 5, faisant appel à Scratch (et même précisément à la version 2.0), était plus prévisible. Il n’en est pas moins innovant parce que les déplacements ne sont pas de type « tortue » mais de vraies translations y sont appliquées au chat.
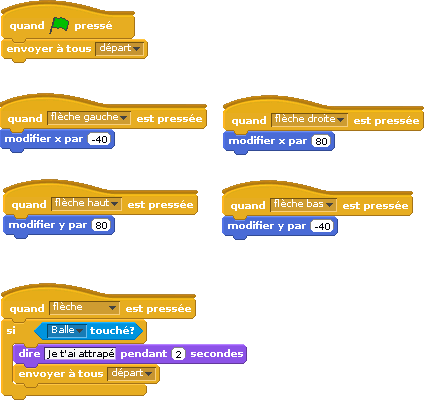
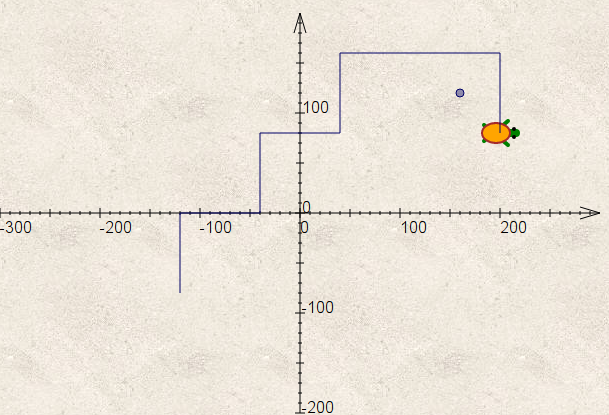
Voici la position de départ du jeu : Le chat est en (-120 ;-80) et la balle est en (160,120) :

Les variables x et y sont les coordonnées du chat (il vaut mieux le savoir si on veut faire la suite de l’exercice). Les flèches ont donc pour effet de faire avancer ou reculer le chat parallèlement à l’un des axes de coordonnées. Donc un appui sur la flèche droite suivi d’un appui sur la flèche gauche a pour effet que le chat va avancer de 80 pixels puis reculer de 40 pixels : Il ne sera donc pas au point de départ.
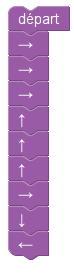
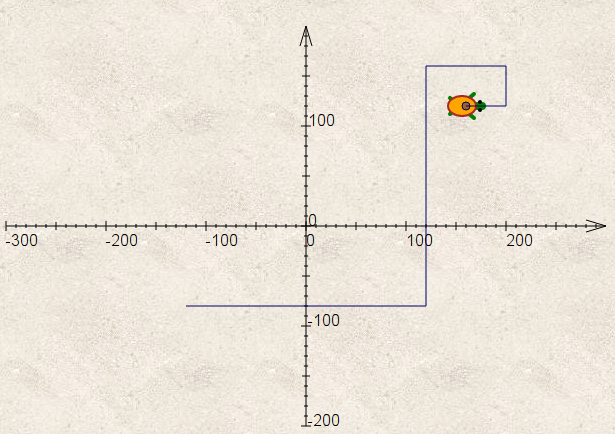
Le raisonnement ci-dessus permet de suivre le chemin effectué par le chat si on appuie sur ces touches :

Le parcours montre que les coordonnées finales sont (0 ;-40) :

Pour le QCM, là encore, il y a un implicite : Le chat est supposé de retour au point de départ. C’est peut-être évident pour le rédacteur du sujet, ça l’est peut-être moins pour les candidats...
Maroc
Le sujet Centres étrangers comportait lui aussi un exercice sur Scratch, mais en fait c’était un exercice portant essentiellement sur une tâche complexe et de la géométrie.
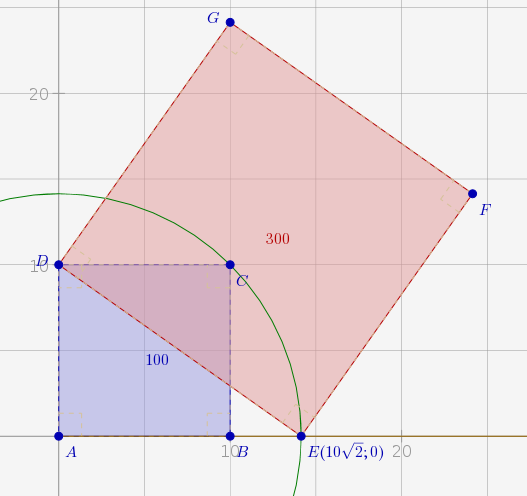
Une maison était définie, au départ, comme un quadrilatère ouvert ou un pentagone privé d’un de ses côtés, défini ainsi :

L’affichage de l’abscisse donne bien, comme il était demandé de le vérifier, environ 71 :
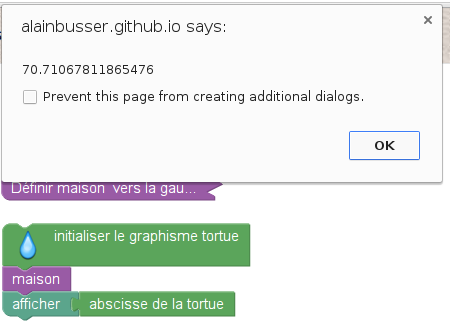
On ne peut tracer que 5 maisons comme le montre ce script avec affichage des abscisses directement sur le dessin :

Le dessin obtenu autovalide le script, en passant :

La dernière question donne lieu à des modifications non précisées dans l’énoncé : Les maisons simplifiées avaient des toits inclinés à 45°, il est évident que le nouvelles maisons ont des toits inclinés à 30° :
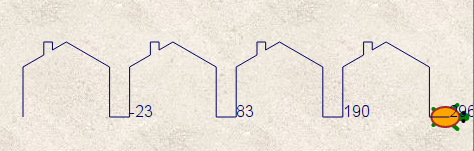
Outre les modifications d’angles, il fallait remplacer dans le script « initial », le bloc mis en exergue, par les 9 blocs de droite :
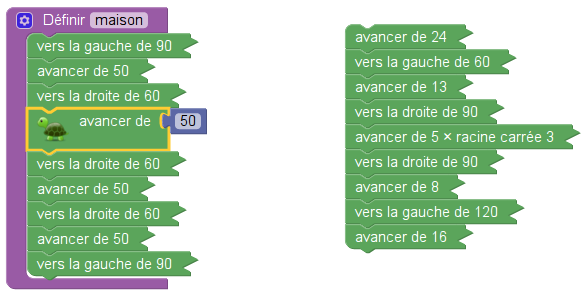
On y voit que EM=8, MC=13 (calculés par trigonométrie) et HE=5√3.
Ceci pose la question du sens du mot calculer de la dernière question : S’agissait-il comme dans la première question, de donner un résultat arrondi à l’entier ? Fallait-il arrondir autrement ? La réponse exacte devait-elle être écrite comme 5√3 ou pouvait-on écrire √75 ?
Polynésie
série générale
Le sujet est disponible ici
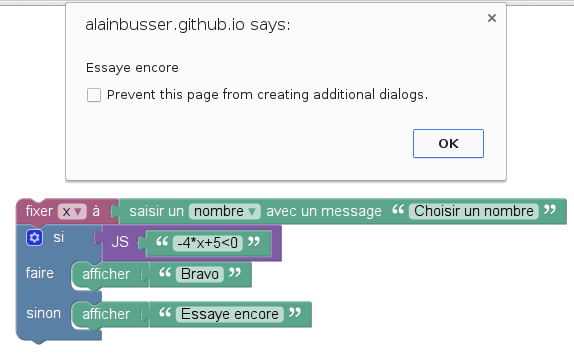
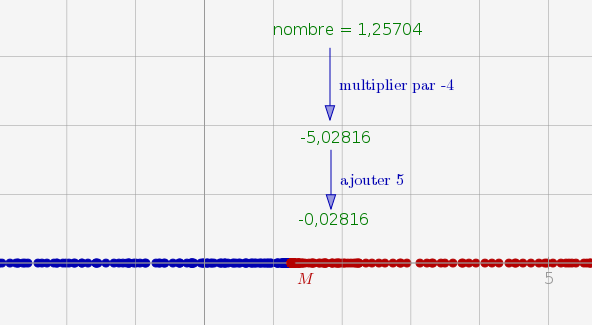
Encore un programme de calcul :
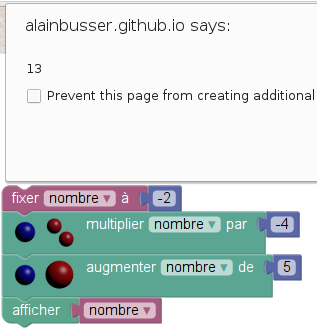
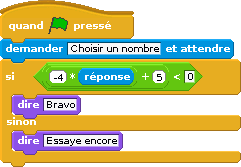
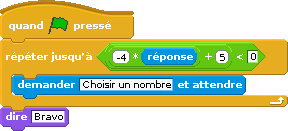
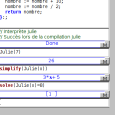
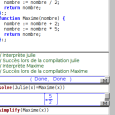
En fait la fonction ainsi programmée est affine (on se sert de ce résultat pour la suite) :

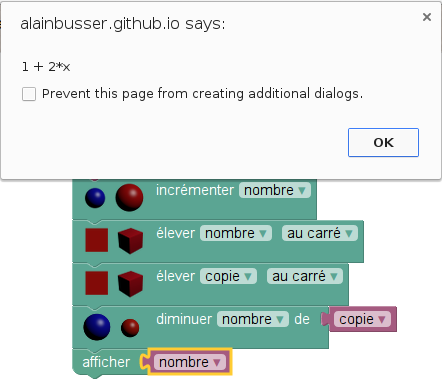
Pour savoir quel nombre on doit choisir au départ pour avoir à -3 l’arrivée, on peut fabriquer une équation en concaténant les -4x+5 avec le texte « =-3 » ; La chaîne de caractères ainsi obtenue (ici, -4x+5=-3) est une équation, qu’il suffit ensuite de résoudre :
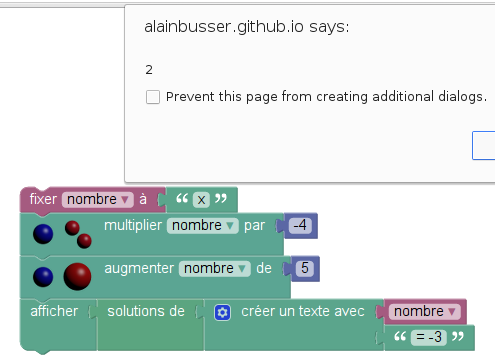
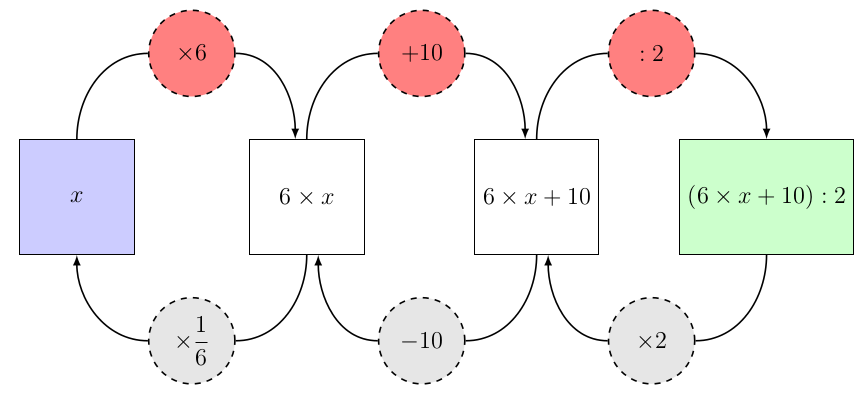
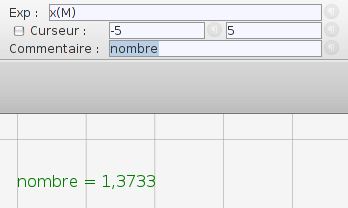
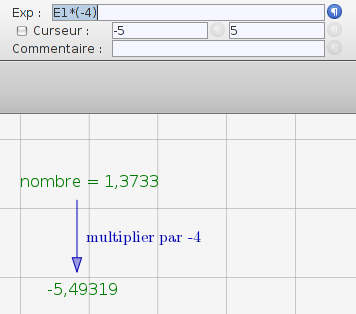
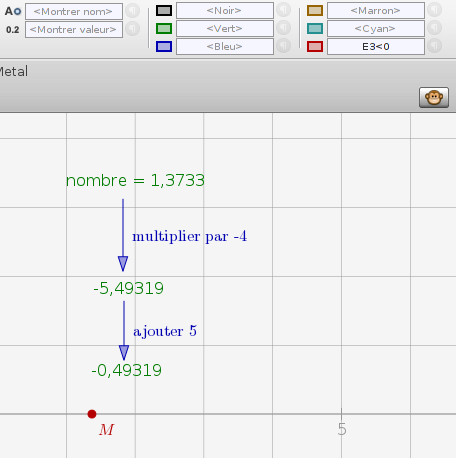
Comme on l’a vu dans l’onglet sur Pondichéry, on pouvait aussi « remonter les calculs », en suivant ce plan :
- Si on a -3 après avoir augmenté de 5, c’est qu’on avait -8 avant ;
- Si on a -8 après avoir multiplié par -4, c’est qu’on avait 2 avant.
série professionnelle
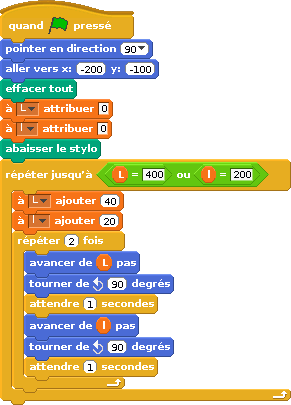
Dans le sujet du brevet professionnel, il y avait un long script de déplacement (le chat imitait un drone, on n’est pas certain que la ressemblance soit frappante !)
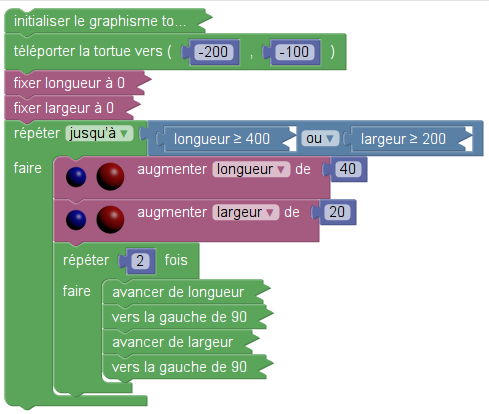
| Version Scratch simplifiée | Version Sofus |
|
|
Dans Sofus, c’est la tortue qui se prend pour un drone, mais l’énoncé disait bien qu’on teste le drone. D’ailleurs un drone qui « efface tout », ça fait un peu peur : On se demande si on veut vraiment garer son vélo sous un tel drone...
Voici le dessin tracé :

Bref, ce drone parcourt des rectangles. Et il en parcourt 10 puisque 400=40×10.
Asie
Le sujet est disponible ici.
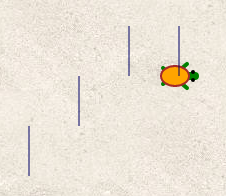
Encore un programme de déplacement de tortue, et encore un qui se situe en dehors du paradigme de la tortue puisqu’il est fait assez explicitement usage, au lieu des rotations de la tortue, d’une boussole, ou plutôt d’une rose des vents :
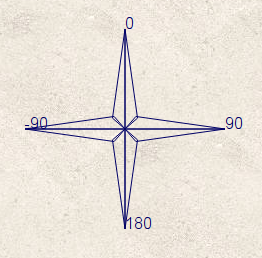
Margot a écrit un programme permettant de faire des dessins à l’aide des touches ↑, → et ↓ du sujet d’Amérique du Nord (exercice 5, voir onglet « USA » : Il manque ici la touche « vers la gauche »). Par défaut les déplacements du lutin laissent des traits sur l’écran, mais pour obtenir cela, le stylo est baissé à chaque déplacement puis relevé après, systématiquement. Le programme aurait été plus simple si le stylo était tout le temps baissé, mais lorsqu’on téléporte le lutin de Scratch dans le bloc initialisation, il laisserait une trace si son stylo était baissé : La téléportation se fait, sous Scratch, au ras de l’écran, et pas par le cycle dématérialisation/rematérialisation immortalisé par Monsieur Spock...
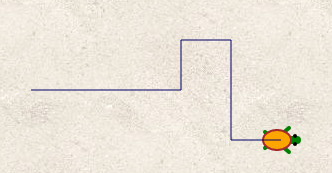
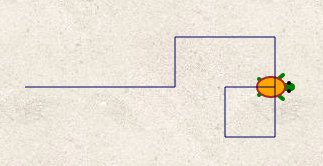
Le sujet, comme celui d’Amérique du Nord, présente un programme (de déplacement) sous forme d’un mot (sur l’alphabet ↑, → , ↓) et, comme dans l’onglet « USA » on va ici écrire ces mots plutôt que décrire des séquences d’appui de touches [7]. Voici les trois dessins du sujet, avec les mots les traçant :
|
|
|
|

|

|
Métropole
Le sujet de juin Métropole/Réunion comportait un exercice pas trop difficile, comportant de belles figures. On va donc ici en profiter pour proposer quelques prolongements.
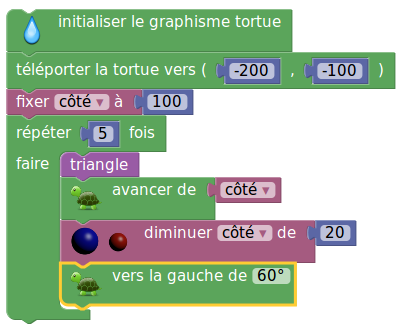
Voici la version Sofus du script de l’énoncé :
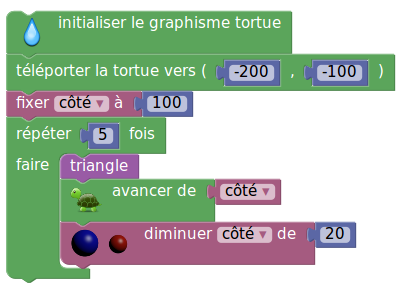
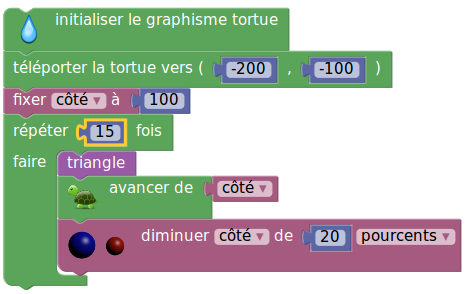
La seconde ligne (3e sur la version Scratch) comprend les coordonnées demandées dans le sujet, mais on remarque que leur notation est plus cohérente avec celle du cours de maths, que celle de Scratch : Aller à x : -200 y : -100 qui semble héritée de la programmation objet, ce qui nécessite un effort de lecture.
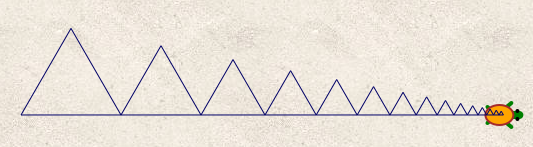
Le script fait ce dessin :
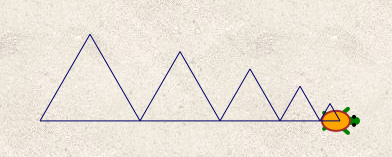
On y voit les 5 triangles dessinés (information qui elle aussi se lisait dans le script : C’est le nombre de répétitions).
Dans la version Sofus, la variable côté est diminuée de 20, alors que dans la version Scratch, on lui ajoute -20 : Cette version, moins naturelle [8], donne lieu à une question qui aurait perdu son intérêt avec la version Sofus : Quelle est la longueur du côté du deuxième triangle ?. On trouve bien sûr 80...
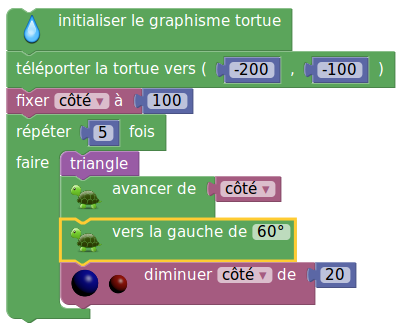
Pour obtenir cette figure :
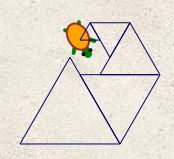
il n’y avait qu’un bloc à ajouter.
Sujet section professionnelle
Savoureux style littéraire que permet l’allusion à Scratch sans le citer :
Le chat doit dessiner le podium ci-dessous constitué de trois plots numérotés de 1 à 3 :

En effet dans le monde de Scratch, non seulement les chats savent dessiner, mais en plus ils doivent le faire ! On se permettra ici, une fois encore, de préférer le paradigme de la tortue de Papert, que l’on pouvait, à l’aide d’un stylo, transformer en table traçante, et qui sera vue de dessus afin de permettre de voir à la fois la tortue et son plan de travail (là où elle dessine) [9].
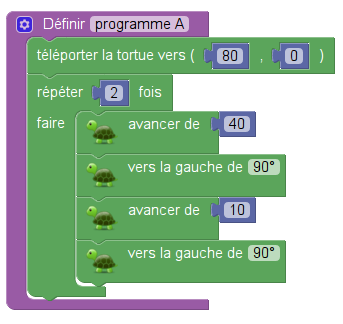
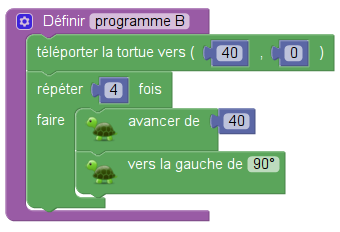
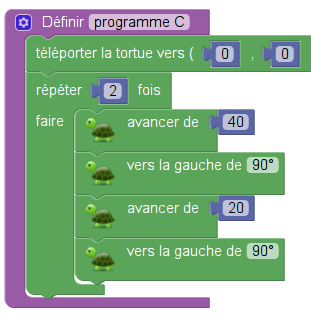
Le but de l’exercice était de programmer ces trois tracés de rectangles, d’une part avec un QCM à deux choix, demandant de déterminer quel programme trace quel rectangle, et ensuite avec une modification demandée à l’un des programmes (le A) pour avoir le programme (qu’on appellera C ici) dessinant le troisième rectangle.
On constate que la première question portait sur une relation, ou plus précisément une application entre
- l’ensemble des programmes (tout au moins A et B) ;
- l’ensemble des rectangles.
L’objet de cet exercice était donc de mettre en relation, d’une part A et 3, d’autre part B et 2. Ce qui peut aisément se représenter par un diagramme sagittal de ce genre :
| A ⟶ 3 B ⟶ 2 |
C’est peut-être l’occasion de remettre au programme les notions de théorie des graphes qui prévalaient à l’époque des « maths modernes » et plus particulièrement les ensembles et les relations, représentées par diagrammes sagittaux...
Septembre
Il y a eu deux sujets en septembre : L’un, en métropole, portait sur des dessins, l’autre en Polynésie, portait sur un étrange programme de calcul d’une seule ligne. Le sujet de Métropole montrait trois dessins :
| figure 1 | 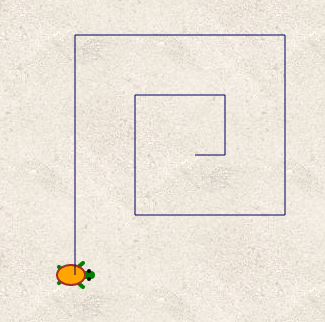
|
| figure 2 | 
|
| figure 3 | 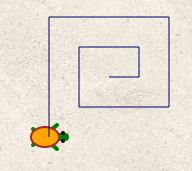
|
(ici représentés avec la tortue, ce qui permet à la fois de simplifier les scripts et de répondre graphiquement à une des questions suivantes)
Ensuite on rappelle que le bloc s’orienter à 90° « signifie que l’on s’oriente vers la droite avec le stylo » [10].
Ensuite l’énoncé définissait un bloc de cette manière :
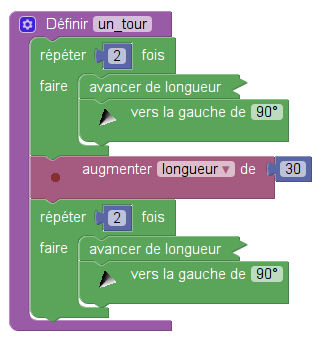
puis s’en servait dans ce script :

Puis on demandait de dessiner l’effet du bloc, avec une initialisation de la variable globale à 30 [11] ; ensuite sans justification l’orientation finale du lutin ; ensuite laquelle des figures 1 et 3 le programme ci-dessus permet-il d’obtenir. Là on conçoit la possibilité de répondre sans avoir Scratch devant soi : La figure 1 suppose une augmentation de la longueur à chaque avancée du lutin, ce qui l’élimine. Mais on voit que la notion de variable est supposée mieux maîtrisée au brevet qu’elle ne l’est, dans les faits, en Seconde. La même exigence se retrouvera dans le sujet de novembre traité dans l’onglet suivant, avec d’ailleurs le même nom longueur pour la variable.
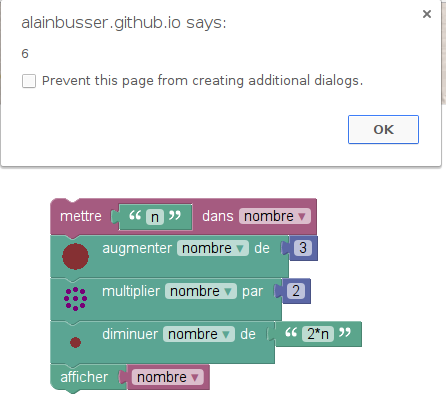
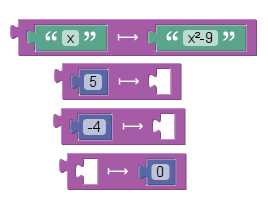
Voici donc le programme de calcul de Polynésie :
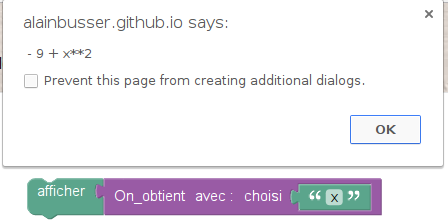
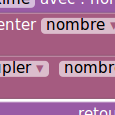
- on affiche le texte « choisis un nombre »
- on attend l’entrée d’un nombre x
- on met le nombre x²-9 dans y
- on affiche y
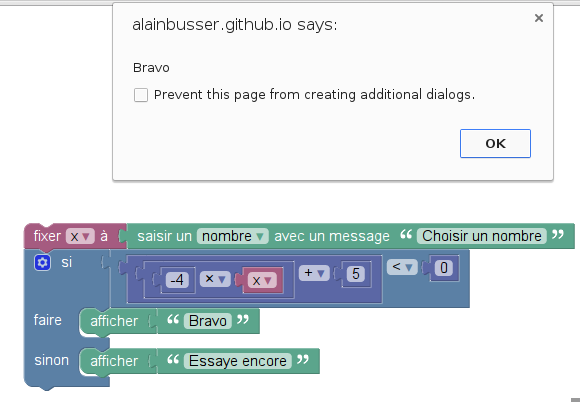
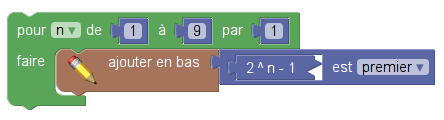
En dehors de tous ces affichages et entrées de données, il y a un programme de calcul mais en une seule étape : Mettre x²-9 dans y. La version Blockly permet de détailler un peu ce programme de calcul sans trop alourdir le script :

Novembre
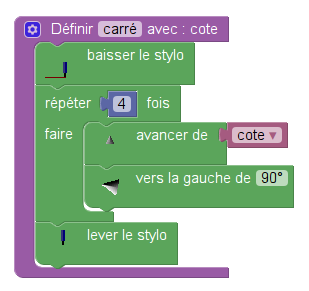
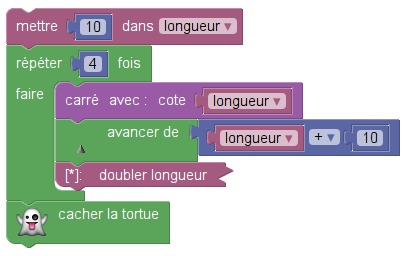
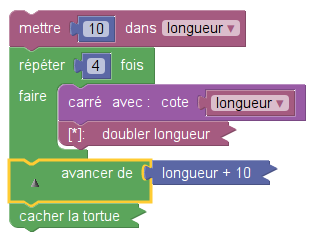
Le sujet d’Amérique du Sud comportait deux programmes mais aussi une définition de bloc :
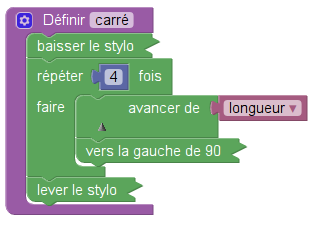
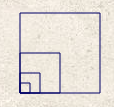
On comprend que ce bloc fait dessiner par le lutin un carré de côté longueur, la longueur en question étant une variable. En l’occurence cette variable est globale. Et elle varie dans les deux programmes :
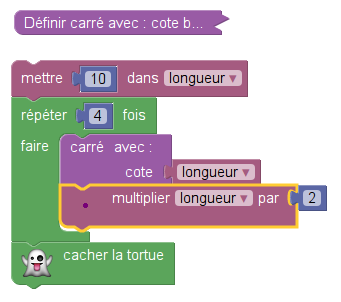
| Programme n° 1 | 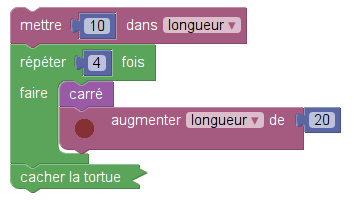
|
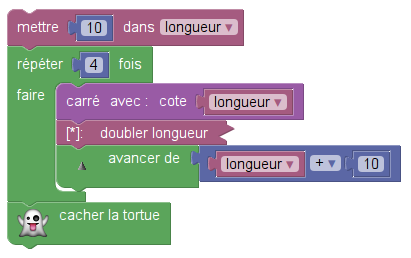
| Programme n° 2 | 
|
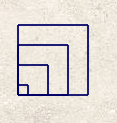
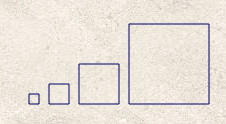
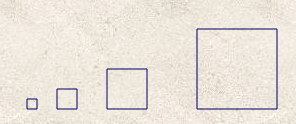
La question « Pour chacun des deux programmes, déterminer la longueur, en pixel, du côté du plus grand carré dessiné ? » est une question classique sur les programmes de calcul (quelle est la valeur finale de la variable longueur ?). Mais placée dans un contexte graphique,
- ou bien cela complexifie la question déjà pas si simple (il y a tout de même des boucles dans le programme de calcul)
- ou alors le contexte graphique rend au contraire plus facile la réflexion sur l’exercice parce que celle-ci porte sur des grandeurs géométriques et non sur des nombres abstraits.
Ce serait intéressant de connaître le taux de succès de cet exercice lors de la correction des copies.
Décembre
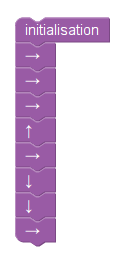
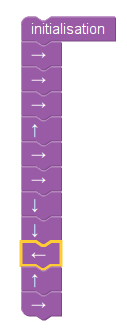
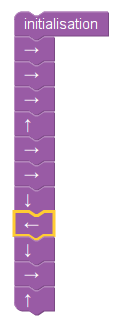
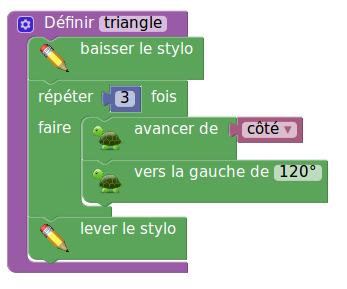
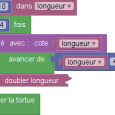
Le sujet de Wallis et Futuna comportait un exercice assez court sur Scratch. Il y avait un programme Scratch à compléter (donné en annexe au sujet). Outre la difficulté superflue de l’explication de s’orienter à 90°, une partie de l’énoncé surprend, celle justement du programme à compléter (dessiner un losange), décrite dans l’énoncé par « le bloc Losange » donné en titre d’une figure comportant pas moins de 11 blocs ! En fait, la définition des blocs par Blockly utilise la forme en « C » qui permet effectivement de ne voir qu’un bloc (celui qui englobe les autres ;en mauve) :
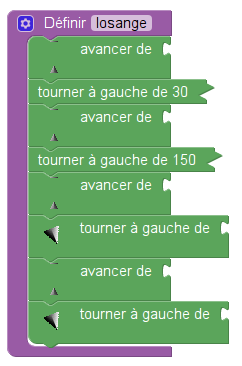
Une fois qu’on sait (ou pas) comment dessiner le losange, on veut s’en servir pour dessiner une fleur (très classique depuis Logo) que voici :
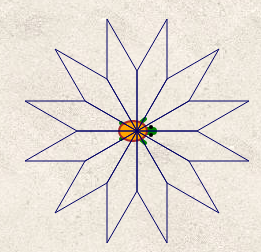
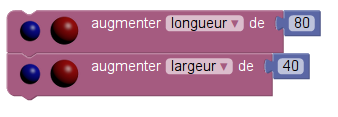
Pour cela, on donne quatre blocs (dont le losange précédemment défini) parmi lesquels on devait « indiquer ... dans l’ordre, les deux instructions à placer dans la boucle » :
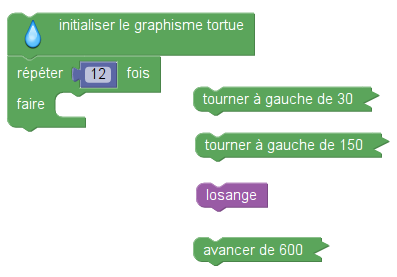
Répondre au hasard c’est choisir undes 12 couples de blocs possibles parmi ces 4. Mais les 4 couples suivants dessinent la fleur :

L’exercice était donc plus facile qu’il en avait l’air (et néanmoins noté sur 5 points) mais une fois de plus, même si l’énoncé ne cite ni Scratch ni le lutin, des connaissances sur un outil bien précis étaient requises (orientation à 90°, habitude de lever le crayon spécifique à Scratch, et inutile ici, définition d’un bloc sous forme de plusieurs blocs...)
Le sujet de Nouvelle-Calédonie ne comportait aucun exercice sur Scratch mais un programme de calcul y figurait. Pas n’importe quel programme de calcul : Celui qui a été traité avec la logique de Hoare et le calcul formel que voici (Sofus 2.0) :
Cette première année de présence de Scratch au collège laisse quand même bien des questions :
- Le choix de ce logiciel de programmation visuelle était-il pertinent, notamment comparé à Blockly qui permet de définir des fonctions ?
- Les programmes de calcul gagnent-ils à être traités par Scratch, avec des affichages multiples qui brouillent la visibilité du programme ?
- Le lutin par défaut, qui dessine sur un plan situé verticalement derrière lui, est-il vraiment plus pertinent qu’un lutin vu d’au-dessus, laissant une trace sur le plan où il se déplace ?
- Pourquoi les exercices portant sur les coordonnées sont-ils si nombreux alors que l’univers naturel des lutins est la suite de mouvements relatifs ?
- Les exercices faits avec Scratch ne pouvaient-ils pas être faits, voire mieux faits, sans Scratch ?
- Est-on certain de ne pas attendre des élèves une « expertise sur un logiciel particulier » que cherche justement à éviter le document ressource ?
- Que signifie l’expression « s’orienter avec le stylo ? »




















Commentaires