la première chose à faire est d’importer la fameuse méthode d’échantillonnage ; elle appartient à l’objet random de Python, donc il suffit d’écrire

from random import sample

Mais, pour éviter de bousculer les habitudes des élèves, on lui a préféré l’import complet de l’objet random :

from random import *

Ensuite, c’est le moment de construire le jeu de cartes, en définissant d’abord la liste des valeurs de cartes :

valeurs=['1','7','8','9','10','V','D','R']

Pour la liste des couleurs, la gestion d’Unicode par Python 3 a permis d’abréger les affichages, en codant chaque couleur par un seul caractère :

couleurs=['\u2665',\u2666','\u2663','\u2660']

Les unicodes correspondants représentant respectivement les carreau (carte à jouer), cœur (carte à jouer), pique (carte à jouer) et trèfle (carte à jouer). Un jeu de 32 cartes peut alors être constitué en accolant une valeur et une couleur, séparées par un blanc, pour toutes les valeurs et couleurs possibles :

omega=[v+' '+c for v in valeurs for c in couleurs]

On constate que cette fois-ci, l’univers de probabilités n’est pas un ensemble comme il se devrait, mais une liste. Ce choix, incorrect du point de vue mathématique [1], est celui de l’algorithme utilisé par Python pour échantillonner [2]. Pour obtenir une main au poker (c’est-à-dire un échantillon de 5 cartes), il suffit alors de faire

main=sample(omega,5)
print(main)

Bref, l’ébauche d’un simulateur de jeu de poker à 32 cartes prend 5 lignes de Python (la main est devenue un jeu, pour éviter de confondre avec le processus principal ou main thread) :

Pour voir si on a de la chance au jeu, on peut compter les as en affichant uniquement la première lettre de chaque carte, avec

[carte[0] for carte in main]

En effet, la première lettre d’un mot est rangée dans le mot à l’index 0, ce qui est d’ailleurs un vieil usage en informatique :

Le problème est que deux cartes différentes commencent par « 1 » : L’as et le dix. Plusieurs élèves ont circonvenu cette difficulté en remplaçant le « 1 » par un « A » pour l’as, mais pour éviter ce genre de problème, on a continué en comptant les dames. Les héroïnes de ce TP ont donc été Judith, Rachel, Pallas et Argine.

Puisque

[carte[0] for carte in main]

donne la liste des premières lettres de la main,

[carte[0] for carte in main].count('D')

donne le nombre de dames dans la main de 5 cartes. Question posée aux élèves : « Quelle est la probabilité que ce nombre soit égal à 5 ? » [3]

Ensuite, on peut répéter l’expérience pour voir si on a souvent de la chance avec les dames [4] :

On voit que souvent on n’a pas de dame du tout [5]. En fait, l’absence de dame dans le jeu est constatée dans environ la moitié des cas.

Ensuite, une question a été posée pour préparer le cours :

« Monsieur Jean-Luc est candidat à des élections dans une ville de 10 000 électeurs ; sur les 10 000, 15 % veulent voter pour lui (mais il ne le sait pas). Il commande un sondage, où on interroge 100 personnes au hasard. Est-il vrai que 15 personnes voteront pour Monsieur Jean-Luc parmi les 100 ? »

De façon analogue à l’exemple des cartes à jouer, l’univers de probabilité est codé par une liste ; mais elle contient 10000 éléments (ce qui est quand même beaucoup plus que 32 !) et on la construit en combinant linéairement deux listes à un seul élément ([’pour’], multipliée par 1500, et [’contre’], multipliée par 8500) :

population=['pour']*1500+['contre']*8500

Pour vérifier qu’on ne s’est pas trompé, afficher la liste population est peu utile, mais on peut demander à Python de compter le nombre d’habitants de la ville, avec len qui fournit le nombre d’éléments d’une liste.

Ensuite, on simule un sondage sur 100 personnes avec

echantillon=sample(population,100)

et on peut afficher le nombre d’électeurs favorables à Monsieur Jean-Luc dans l’échantillon :

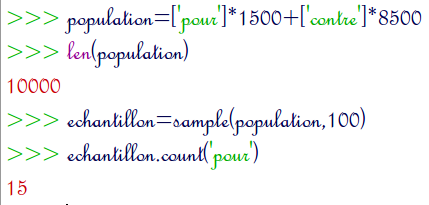
Moins de la moitié des élèves ont eu l’affichage 15, mais très peu ont eu un affichage inférieur à 13 ou supérieur à 17 : La suite de l’histoire aura lieu dans le cours sur les intervalles de fluctuation. Pour Monsieur Jean-Luc, évidemment, la suite de l’histoire, ce sont les élections, où on vérifiera si le pourcentage d’électeurs qui lui sont favorables est vraiment 15%, mais ceci est une autre histoire...

Le temps le permettant, le TP s’est prolongé par la sempiternelle question : « Où sont les dames ? »

On peut utiliser la loi des grands nombres pour estimer les probabilités d’avoir un certain nombre de dames dans le jeu, par des mesures de fréquences. Pour cela on effectue 1000 tirages, mais plutôt que les afficher tous, on va les stocker dans une liste appelée listejeux :

listejeux=[sample(omega,5) for n in range(1000)]

Seulement, puisque chaque jeu (ou main) est une liste de 5 cartes, listejeux est une liste de listes, et pour accéder à un jeu, il faut utiliser un indice (ici, le premier des 1000 jeux) :

La liste complète est longue

mais l’affichage (long lui aussi) a quelque chose d’artistique :

Ainsi, pour chaque élément de listejeux (l’élément listejeux[n]), on crée comme précédemment la liste des premières lettres, et on compte ses dames (la lettre ’D’) ; on stocke le tout dans une liste d’entiers appelée listedames :

listedames=[[c[0] for c in listejeux[n]].count('D') for n in range(1000)]

Puis on crée par comptage des 0, des 1, des 2 etc. une liste d’effectifs :

[listedames.count(n) for n in range(5)]

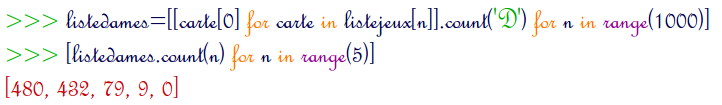
Avec 10000 parties, on constate

• que dans environ 49% des cas, il n’y a aucune dame ;
• que dans environ 40% des cas, il y a exactement une dame ;
• que les paires de dames (2 dames exactement) apparaissent dans environ 10% des cas ;
• que les brelans (3 dames) sont très rares (environ 0,7 ou 0,8%)
• que les carrés (les 4 dames) sont exceptionnels

On peut faire une application de la probabilité au poker en cherchant les valeurs exactes des fréquences remarquables trouvées ci-devant.

1. Tout d’abord, le nombre de manières de choisir 5 cartes parmi 32 (le dénominateur des probabilités) est 201 376 [6]
2. Pour avoir la probabilité de n’obtenir aucune dame, il faut diviser par ce dénominateur, le nombre de manières de choisir 5 cartes parmi 28 (les cartes autres que des dames) ; ce qui donne 1755 chances sur 3596, soit environ 0,488.
3. Pour avoir la probabilité de n’avoir que la dame de cœur, on divise par 201 376, le nombre de manières de choisir 4 cartes (celles qui restent quand on a pris la dame de cœur) parmi les 28 restantes. Le nombre obtenu est à multiplier par 4 pour avoir la probabilité d’avoir exactement une dame ; on trouve 2925 chances sur 7192, soit environ 0,4067.
4. Pour avoir la probabilité d’une paire de dames, on multiplie le nombre de manières de choisir les deux dames en question parmi 4, par le nombre de manières de choisir les trois cartes restantes parmi les 28 qui ne sont pas des dames, et on divise par 201 376 ; ce qui donne 351 chances sur 3596, soit environ 0,0976.
5. Pour avoir la probabilité d’un brelan (trois dames), on divise par 201 376, le nombre de manières de choisir les deux dernières cartes parmi les 28 qui ne sont pas des dames, multiplié par 4 puisqu’il y a 4 dames qui peuvent être exclues du brelan ; ce qui donne 27 chances sur 3596, soit environ 0,0075.
6. Enfin pour avoir la probabilité d’avoir un carré de dames (les 4 dames), on divise par 201 376, le nombre de manières de choisir la cinquième carte parmi les 28 qui ne sont pas des dames ; on trouve une chance sur 7192, soit environ 0,00014.

Le tableau calculé avec la précision de Python 3 est ici :

On voit que l’estimation de « une chance sur deux de ne pas avoir de dame » était légèrement surévaluée, que la probabilité de 0,4 pour la dame unique était sous-évaluée, et que le « une chance sur dix d’avoir une paire de dames » était sous-évaluée (mais à peine).