Le développement de $\frac{\sqrt{2}}{2}=\frac{1}{\sqrt{2}}$ (qu’on va appeler r dans la suite de l’article) en fraction continue est, comme on peut le vérifier par la suite de calculs (autrement dit, l’algorithme) qui le produit, égal à ceci :

[0,1,2,2,2,2,2,2,...]

La suite des réduites de ce développement en fraction continue est source d’approximations rationnelles de r au sens où c’est une suite de fractions convergeant vers r.

On trouve successivement

$$\frac{1}{1}=1$$

$$\frac{1}{1+1}=\frac{1}{2}$$

$$\frac{1}{1+\frac{1}{2+\frac{1}{2}}}=\frac{5}{7}$$

$$\frac{1}{1+\frac{1}{2+\frac{1}{2+\frac{1}{2}}}}=\frac{12}{17}$$

etc.

Chacune de ces fractions est optimale dans le sens où toutes les fractions dont le dénominateur est inférieur ou égal au sien sont au moins aussi éloignées qu’elle du nombre r.

La convergence de l’algorithme est moyennement rapide, l’erreur d’approximation en remplaçant r par la nième fraction étant environ inversement proportionnelle au carré de n :

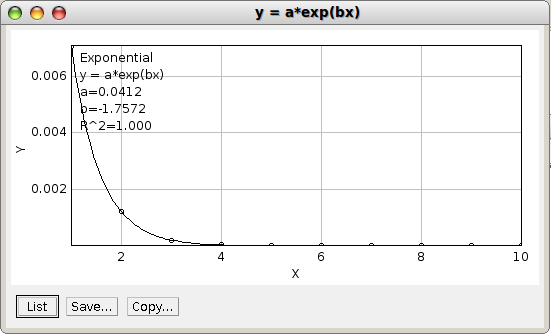
(figure préparée avec l’interpolateur d’ImageJ)

Dans le cas présent, parce que le nombre r est algébrique, le développement en fraction continue est prépériodique ; et parce que c’est une racine carrée, l’algorithme de Heron peut lui aussi fournir une suite d’approximations rationnelles de r. Et même plusieurs, puisque les fractions obtenues dépendent de la valeur initiale. La suite récurrente est donnée par $u_{n+1}=\frac{u_n+\frac{1}{2u_n}}{2}$ ; par exemple, avec $u_0=1$, on a successivement

$1\mapsto \frac{3}{4}\mapsto \frac{17}{24}\mapsto \frac{577}{816}\mapsto \frac{665857}{941664}\mapsto \frac{886731088897}{1254027132096}\mapsto \frac{1572584048032918633353217}{2223969688699736275876224}$

La taille des fractions suggère une convergence très rapide, comme le confirme l’interpolateur de ImageJ avec une erreur d’approximation inversement proportionnelle à la puissance cinquième du rang :

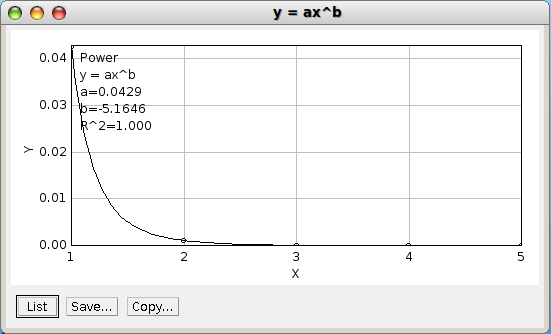
Résultat classique : On a doublement du nombre de décimales correctes à chaque itération.

Bien que très rapidement convergent, l’algorithme de Heron présente l’inconvénient de ne pas s’appliquer à tous les réels : L’algorithme manque de généralité. De plus, on peut souhaiter une valeur approchée un peu moins bonne mais avec un dénominateur plus petit...

En 1816, John Farey (1766-1826) fait une remarque de mathématicien amateur (il était géologue) : Lorsqu’on écrit dans l’ordre croissant toutes les fractions (irréductibles) inférieures à 1 de dénominateur inférieur ou égal à un entier donné, chaque fraction est la médiante de Farey des deux fractions qui l’entourent : La fraction dont le numérateur est la somme des numérateurs des fractions l’entourant, et dont le dénominateur est la somme des dénominateurs.

Les fractions de Farey donnent un algorithme très simple pour approcher un réel par des rationnels : On fait comme l’algorithme de dichotomie, sauf qu’au lieu de la moyenne des deux bornes de l’encadrement, on prend leur médiante de Farey. Par exemple, comme r est dans l’intervalle [0,1],

1. on commence par calculer leur médiante, qui est $\frac{0+1}{1+1}=\frac{1}{2}$ ; on la compare à r : elle lui est inférieure, donc on remplace la borne inférieure $\frac{0}{1}$ par $\frac{1}{2}$ : $\frac{1}{2}
2. on recommence, avec le calcul de la médiante $\frac{1+1}{2+1}=\frac{2}{3}$ ; comme $\frac{2}{3}
3. on continue : la médiante de Farey des deux bornes est $\frac{2+1}{3+1}=\frac{3}{4}$ : Cette fois-ci, $r<\frac{3}{4}$ donc c’est la borne supérieure qu’on remplace par la médiante ; l’encadrement devient $\frac{2}{3}
4. la nouvelle médiante est $\frac{5}{7}$ ; etc.

L’algorithme a été évoqué pour la première fois en 1858 par Moritz Stern, professeur de mathématiques à Göttingen, dans un article en Allemand. Stern était spécialiste de la théorie des nombres (il a eu Riemann comme élève).

Mais indépendamment de ces recherches prussiennes, Achille Brocot, horloger français, redécouvrait l’algorithme (pour la conception de rouages) et le publiait en 1861 dans la revue chronométrique, une revue professionnelle réservée aux horlogers, sous le titre Calcul des rouages par approximation, nouvelle méthode. Aussi l’algorithme est-il appelé algorithme de Stern-Brocot.

Dans le cas présent, les fractions peuvent être calculées en quelques lignes de Ruby :

require 'mathn'
r=Math.sqrt(2)/2
a ,b = 0,1
40.times do [
	m=(a.numerator+b.numerator)/(a.denominator+b.denominator),
	if m<r then a=m else b=m end,
	puts(m),
	]
end

L’algorithme de Stern-Brocot converge assez lentement, moins vite que les fractions continues :

Et c’est normal, puisque les approximations par fractions continues se trouvent dans la suite des réduites de Stern-Brocot. On remarque que les fractions données par l’algorithme de Heron figurent aussi dans la liste des réduites de Stern-Brocot.

Dans l’onglet précédent, on a vu comment, à partir de deux fractions $\frac{a}{b}$ et $\frac{c}{d}$, obtenir une meilleure approximation $\frac{a+c}{b+d}$ du réel. En écrivant la matrice des deux fractions $\left( \begin{array}{rr} a & c \\ b & d \end{array}\right)$, on constate qu’il suffit de la multiplier à droite par $\left(\begin{array}{r}1 \\ 1 \end{array} \right)$ pour obtenir la médiante $\left(\begin{array}{r} a+c \\ b+d \end{array} \right)$ des deux fractions.

Or chaque étape de l’algorithme de Stern-Brocot consiste à remplacer une, et une seule des deux fractions (une des deux colonnes de la matrice) par la médiante. Plus précisément, à partir d’un encadrement entre $\frac{a}{b}$ et $\frac{c}{d}$, représenté par la matrice $\left( \begin{array}{rr} a & c \\ b & d \end{array}\right)$,

1. Si la médiante est plus petite que le nombre à approcher, on remplace la première colonne de la matrice par la médiante, ce qui revient à multiplier la matrice par $G=\left( \begin{array}{rr} 1 & 0 \\ 1 & 1 \end{array}\right)$ ;
2. Si la médiante est plus grande que le nombre à approcher, la matrice représentant l’intervalle est à multiplier par $D=\left( \begin{array}{rr} 1 & 1 \\ 0 & 1 \end{array}\right)$, pour remplacer sa deuxième colonne par la médiante.

Tout réel entre 0 et 1 peut être représenté de façon unique par une suite de matrices G et D par lesquelles on doit multiplier la colonne $\left( \begin{array}{r}1 \\ 1 \end{array}\right)$ pour avoir les représentations matricielles des approximations successives données par l’algorithme de Stern-Brocot.

Par exemple, pour l’inverse r de la racine de 2, la suite des matrices à multiplier est GGDDGGDDGGDD...

Il s’agit d’un langage régulier (ou RegExp) qui, avec les notations des RegExp, s’écrit (GGDD)*

la chaîne « GGDDGGDDGGDD... » rappelle le développement [1,2,2,2,2,2,...] en fraction continue de r. Ce n’est pas un hasard :

Les nombres apparaissant dans le développement en fraction continue d’un réel sont les nombres de « G » et de « D » successifs (en alternance) dans l’écriture ci-dessus.

Le choix des lettres « G » et « D » n’est pas anodin, comme on le voit dans l’onglet suivant.

Ainsi, tout nombre entre 0 et 1 peut s’écrire comme un mot (éventuellement infini) écrit à l’aide des lettres "G" et "D". Chaque choix binaire entre "G" et "D" peut être représenté par une branche d’un arbre binaire : L’arbre de Stern-Brocot. Le sommet de l’arbre est le milieu $\frac{1}{2}$ de l’intervalle ; le sous-arbre de gauche correspond à tous les réels inférieurs à $\frac{1}{2}$, et les réels de l’intervalle supérieurs à $\frac{1}{2}$ sont représentés par le sous-arbre de droite.

En donnant à l’arbre une structure fractale (les branches de plus en plus petites, convergeant vers le point dont l’abscisse est le nombre à approcher), on peut « voir » les fractions approchant un réel entre 0 et 1 :

Les matrices de l’onglet précédent correspondent à un mouvement vers la gauche de l’arbre (la matrice G) ou vers la droite de l’arbre (la matrice D).

Dans le diaporama CaRMetal téléchargeable en bas de l’article, l’arbre de Stern-Brocot a été construit une fois pour toutes par un CaRScript, basé sur des troncatures de fractions continues, mais un CaRAScript dessine en temps réel et en traits épais la partie de l’arbre qui a été parcourue en appliquant l’algorithme de Stern-Brocot à un nombre réel donné entre 0 et 1. Ce nombre peut dynamiquement être modifié tout simplement en déplaçant à la souris le point dont il est l’abscisse. L’approximation rationnelle du nombre (nécessaire si on veut que l’algorithme s’arrête) est bien entendu calculée par l’algorithme de Stern-Brocot, ce qui permet de regarder comment celui-ci peut être implémenté en JavaScript (notamment, une fraction est codée par un tableau à deux entrées entières).

Si on s’intéresse à un nombre éventuellement supérieur à 1, on remplace la borne supérieure 1 par la fraction infinie, par convention de numérateur 1 et de dénominateur nul. Mais l’algorithme converge alors très lentement si on veut approcher un réel proche de 1.

Si la réalisation de l’algorithme de Stern-Brocot comme CaRAScript permet sous CaRMetal, de piloter des fractions par curseur, la fonction FractionText de GeoGebra (appliquée à un curseur évidemment) évite la nécessité de recourir à l’algorithme de Stern-Brocot. Cette fonction utilise l’affichage LaTeX et le calcul formel incorporé à GeoGebra (Mathpiper, un portage Java de Yacas).

Une question intéressante est alors : « Oui on non, le calcul formel de GeoGebra utilise-t-il l’algorithme de Stern-Brocot ? »

La réponse est négative, d’après le code source de Yacas : les fractions continues sont utilisées, mais avec un test NearRational basé sur une recherche de périodicité dans le développement décimal du réel : En voyant un nombre comme 3,142857142857143 GeoGebra devine qu’il est proche d’une fraction dont le développement décimal admet « 142857 » comme période, et dont le dénominateur est donc 7. Il tronque alors le développement en fraction continue de manière à obtenir une fraction dont le dénominateur est 7.

Bref, parce que l’algorithme des fractions continues converge plus vite que Stern-Brocot, il est utilisé dans GeoGebra, au risque d’avoir des fractions compliquées.

Python (langage) en fait de même :

Bien que 1,2 soit une fraction simple, Python ne s’en rend pas compte. En fait la conversion en fraction par Python est faite en simplifiant la fraction obtenue à partir de l’écriture décimale de 1,2 (dont le dénominateur est une puissance de 10) et comme la représentation interne de 1,2 en binaire est plus compliquée que l’écriture décimale de celui-ci, une petite erreur d’approximation entraîne le résultat affiché.

Ruby donne exactement le même affichage, pour la même raison (la représentation interne des nombres en machine est en fait indépendante du langage puisqu’elle ne dépend que ... de la machine !)

En redimensionnant l’arbre de Stern-Brocot pour que l’ordonnée de chaque point d’embranchement soit la moitié de l’inverse du carré du dénominateur (l’abscisse étant la fraction représentée), on a une version de celui-ci moins lisible que celle ci-dessus (onglet « arbre ») :

Mais avec ces dimensions, il se passe une sorte de miracle : Les cercles centrés sur les points d’embranchement de l’arbre et tangents à l’axe des abscisses, sont tangents entre eux [1] :

Chaque cercle vert ci-dessus est un cercle de Ford, et on peut considérer la figure formée par les cercles de Ford comme dotée d’une sorte de squelette qui est l’arbre de Stern-Brocot. Pour mieux voir les cercles de Ford, on peut les représenter sans le squelette :

Dans le diaporama CaRMetal téléchargeable ci-dessous, un CaRAScript montre cette dualité entre l’arbre de Stern-Brocot et les cercles de Ford, en matérialisant l’algorithme de Stern-Brocot par le parcours d’une sorte d’étincelle électrique passant d’un cercle à un autre cercle, qui lui est tangent (sinon le courant ne passerait pas). Là encore, les cercles de Ford ont été préconstruits et seul leur aspect (les cercles deviennent épais lorsqu’ils sont parcourus par le courant) est modifié par le CaRAScript.

Si maintenant on rapetisse les rayons des cercles de Ford de telle manière que ceux-ci ne soient plus tangents entre eux (mais toujours tangents à l’axe des abscisses), on obtient une figure de ce genre [2] :

Au point où on en est, pourquoi pas enrouler l’intervalle [0,1] autour d’une cardioïde avec la représentation paramétrique ci-dessous ?

$$\left\{\begin{array}{l} x=\frac{cos(2 \pi t)}{2}- \frac{cos(4 \pi t)}{4} \\ y=\frac{sin(2 \pi t)}{2}- \frac{sin(4 \pi t)}{4} \end{array} \right.$$

Qu’obtient-on alors [3] ? L’ensemble de Mandelbrot ! Les nombres 0 et 1 avec leur accumulation de cercles de Ford microscopiques, se retrouvent dans le point de pincement de la cardioïde. Le plus gros cercle de Ford, celui correspondant à $\frac{1}{2}$, se retrouve à gauche de la figure ; et les cercles suivants, correspondant aux fractions $\frac{1}{3}$ et $\frac{2}{3}$, se retrouvent en haut et en bas de l’ensemble de Mandelbrot.

Entre $\frac{1}{2}$ et $\frac{1}{3}$, on trouve leur médiante de Farey $\frac{2}{5}$ :

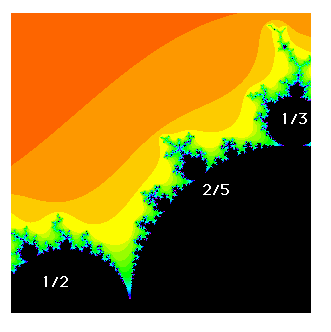
Et entre les deux, la nouvelle médiante $\frac{3}{7}$ [4] :

Ainsi, l’arbre de Stern-Brocot se retrouve même dans l’ensemble de Mandelbrot !

En fait il y a bien plus que l’arbre de Stern-Brocot dans l’ensemble de Mandelbrot (il y a bien plus que la cardioïde) : Au-delà des cercles, se trouvent des ramifications secondaires, à l’infini. Plus de détails ici.

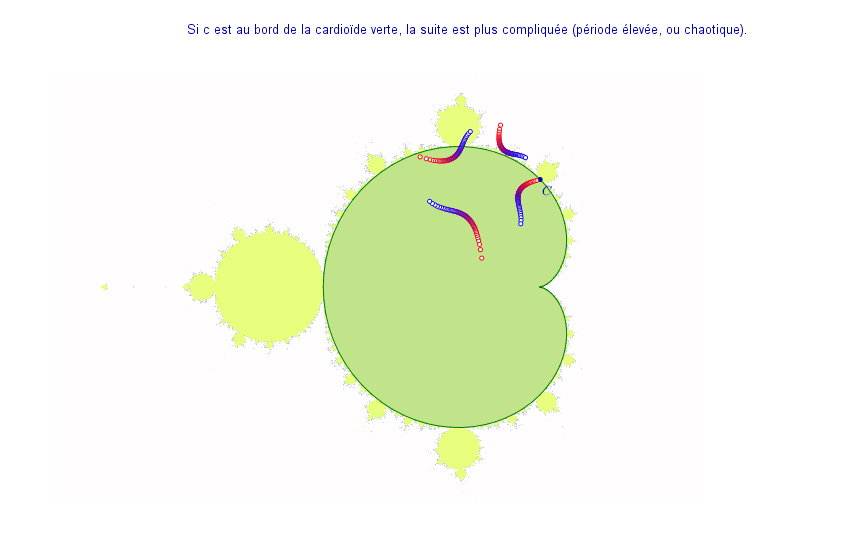
Mais que vient faire l’arbre de Stern-Brocot, qui a trait à des approximations rationnelles de réels, dans l’ensemble de Mandelbrot ? En d’autres termes, où sont les fractions ? L’idée est que lorsque l’ensemble de Julia associé possède une période attractive, chaque point de la période tourne autour du centre de gravité de celle-ci d’un angle qui est une fraction de tour. Cette fraction est le nombre de rotation de l’ensemble de Julia, et parce que la période est attractive, les valeurs de c voisines continuent à avoir une période attractive, avec le même nombre de rotation : La valeur de c pour laquelle on tourne de deux cinquièmes de tours se retrouve en quelque sorte gonflée en un disque qui est attaché à la cardioïde. Ce sont des travaux sur ce thème qui ont valu à Jean-Christophe Yoccoz sa médaille Fields.

Ci-dessus, on a vu dans l’onglet sur les matrices que le parcours effectué dans l’arbre de Stern-Brocot pour approcher un réel par des fractions pouvait être codé par des produits de matrices G et D, les produits partiels représentant des encadrements entre deux fractions de Farey, elles-mêmes représentées par les vecteurs colonnes de la matrice.

Or il est également possible de représenter les fractions irréductibles par des points (les vecteurs colonnes en question), et dans ce cadre, la médiante de Farey est juste la somme des vecteurs joignant l’origine du repère à ces points. La propriété des fractions de Farey sur le déterminant signifie que le quadrilatère (un parallélogramme) dont les sommets sont l’origine du repère, les deux fractions de Farey et leur médiante, a une aire égale à l’unité (cette aire étant la valeur absolue du déterminant).

Par exemple, avec l’encadrement de r donné dans l’onglet sur l’algorithme de Stern-Brocot, le parallélogramme rouge a une aire unité :

Alors les matrices G et D précédentes conservent l’aire et l’algorithme de Stern-Brocot peut être considéré comme une suite de déformations successives du carré unité en des parallélogrammes qui tendent vers la demi-droite d’équation x=ry.

Mais tout parallélogramme de ce genre peut être considéré comme un tore (le plan complexe modulo les deux translations dont les vecteurs ont leurs extrémités représentées en bleu ci-dessus). Le fait que G et D conservent les aires permet de les considérer comme des isométries de l’espace de Teichmuller du tore, lequel n’est autre que le demi-plan de Poincaré (onglet suivant) :

Voilà donc l’arbre de Stern-Brocot également présent dans le plan hyperbolique !

Dans ce cas, toute matrice de déterminant 1 à coefficients entiers (comme le sont les matrices précédentes) devient une isométrie directe parabolique du demi-plan de Poincaré (c’est-à-dire une isométrie laissant invariants des horocycles concentriques, autrement dit, chacune d’entre elles est la composée de deux symétries hyperboliques d’axes parallèles).

La matrice $G$ correspond à l’homographie $z \mapsto \frac{z}{z+1}$, et la matrice $D$ à la translation $z\mapsto z+1$. Dans le premier cas, les horocycles invariants sont les cercles tangents à l’axe des abscisses en son origine, et dans le second cas ce sont les droites horizontales. Dans les deux cas, l’ensemble des cercles de Ford (qui, dans le demi-plan de Poincaré, sont des horocycles) est invariant par chacune des transformations G et D, et donc par le groupe engendré par ces transformations et leurs inverses, qui est en fait le groupe SL(2,Z) de toutes les matrices entières de déterminant 1.

Mais CaRMetal fait de la géométrie hyperbolique dans le disque de Poincaré, pas dans le demi-plan. Dans le disque de Poincaré, la matrice G devient $z\mapsto \frac{(-1-2i) z-1}{z+1-2i}$ et la matrice D devient $z\mapsto \frac{(1-2i) z-1}{z-1-2i}$. À elles deux, elles pavent le plan hyperbolique à partir du domaine fondamental représenté en gris ci-dessous (seule la moitié droite du plan hyperbolique est représentée, pour des raisons de symétrie) :

Ci-dessus seule la moitié des droites du pavage sont représentées, en bleu, ce qui a permis de représenter le pavage dual : L’arbre de Stern-Brocot ! On voit des pinceaux sans support dans cette figure...

L’ensemble des matrices entières de déterminant 1 n’est pas seulement engendré par des isométries directes paraboliques, il l’est aussi par des isométries directes elliptiques (ou rotations), l’une d’ordre 2 (une symétrie centrale), l’autre d’ordre 3. Il en résulte que la courbe modulaire (l’espace de Teichmuller évoqué ci-dessus) peut être assimilé au complémentaire dans l’hypersphère, d’un nœud de trèfle, qui, tracé sur un tore, en fait deux fois le tour dans une direction pendant qu’il en fait trois fois le tour dans l’autre direction. Ceci a permis à Étienne Ghys et Jos Leys d’associer à chacune des matrices vues précédemment, un nœud qui fait le tour de ce fameux nœud de trèfle. Par exemple, pour le passage de la fraction $\frac{1}{1}$ à la fraction $\frac{1}{2}$, le nœud associé est la courbe verte ci-dessous (le nœud de trèfle est représenté en doré) :

La suite des nœuds rencontrés lors d’approximations successives de l’inverse du nombre d’Or est montrée en bas de cet article.