C’est donc assez naturellement que j’ai éprouvé le besoin de réfléchir un peu plus avant sur les différentes formes de savoir, leur interaction, et leur mode d’expansion.

Cela m’amènera à considérer l’élève-professeur comme puisant son savoir dans son statut d’élève pour, petit à petit, se transformer en professeur par une mutation de ce savoir, phénomène que j’ai baptisé depuis « effet chrysalide » et dont la gestion incombe en partie au formateur.

Le lecteur attentif en décernera la douloureuse transformation dans les exemples décrits à la fin de cet article.

Les « savoirs » en présence

Disons que je schématiserais de façon très succincte et sans doute non exhaustive, le cheminement du « savoir » de la façon suivante :

Le « savoir savant » est avant tout opérationnel par rapport à l’inconnu, il favorise les grandes découvertes, il assure la recherche scientifique et il a ses règles propres qui garantissent son efficacité : paradoxes, conjectures, obstacles épistémologiques, schismes d’une part, recherche, traitement de l’erreur, communication d’autre part, en sont les composantes.

Le « savoir élève », lui, est toujours confronté à la connaissance et mis à l’épreuve de celle-ci. Alors que le « savoir savant » ne s’impose que par une cohérence interne validée par la communauté des savants ignorante à priori des contenus de la communication (les anecdotes sur les luttes douloureuses pour obtenir cette reconnaissance jalonnent l’histoire des mathématiques), le « savoir élève » sera toujours validé par une autorité détenant déjà ce savoir.

Cela conduit à d’autres règles de fonctionnement qui, même si elles singent le « savoir savant », y sont radicalement opposées. Certaines portent le même nom : paradoxes, conjectures, recherche ; d’autres ont obtenu des qualificatifs distincts comme : obstacles didactiques, ruptures de contrats.

Le « savoir enseignant » permet au professeur de gérer les apprentissages. Ainsi, mettre l’apprenant en situation de recherche comme le savant, alors qu’il n’est pas un savant, entraîne des dommages collatéraux dont l’influence est non négligeable sur le caractère opérationnel du savoir ainsi acquis ; la gestion, et donc l’évaluation, incombe à l’enseignant.

C’est l’ensemble de ces perturbations qui caractérise pour moi la « transposition didactique ».

À titre d’exemple

La découverte de la 3^e décimale exacte de pi en tant que savoir savant nécessite des contraintes de justification des démarches qui revêtent une signification sans commune mesure avec les exigences de justification que peut développer un élève appliquant un algorithme à cette fin.

Cela explique en grande partie les difficultés rencontrées dans ces activités numériques et l’effort que doit fournir le professeur pour utiliser la transposition didactique non comme frein, mais comme moteur de l’apprentissage.

Dans cet exemple, on peut faire un transfert des intérêts (et non des objectifs) et inviter les élèves à découvrir Archimède, l’Antiquité, ses enjeux, ses problèmes, etc.
Nous voyons ainsi la richesse d’un apport historique dans notre enseignement des mathématiques.

Le fait que le « savoir savant » soit orienté vers l’inconnu alors que le « savoir élève » est orienté vers le connu donne un statut totalement différent à l’erreur, à l’absurde, au paradoxe et à la conjecture.

Le « savoir élève » peut s’accommoder de contradictions invraisemblables que le professeur doit traquer sans relâche comme le montre ce second exemple vécu :

Second exemple

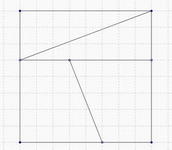
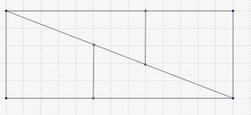
Ci-dessus, on a découpé un rectangle de 5 sur 13 pour en faire un carré de 8 sur 8. Curieusement une aire de 65 se serait transformée en une aire de 64 !

Paradoxe ? Conjecture ? Dans un contexte de « savoir savant », il est clair que l’on n’a pas de carré et que la supercherie est facilement dénoncée.

Dans un contexte de « savoir élève » classique, on peut procéder de même, et on s’attardera alors sur le théorème de Thalès et, partant, sur le sens des nombres.

Mais quid de ces réponses que j’ai eues à gérer avec des étudiants non scientifiques ?

• « C’est normal car le carré a une plus petite surface que le rectangle. »
• « C’est normal, on a découpé… »

Doit-on s’arracher les cheveux en dénonçant le niveau de nos ouailles ? Doit-on embrayer illico par un cours de rattrapage sur la mesure de Radon-Nikodym ? Doit-on rapidement organiser un T.D. sur le Tangram ? Ou bien ne faut-il pas se contenter d’en sourire ?

Saviez-vous que tout triangle a ses trois côtés égaux ?

Prenons un autre exemple de paradoxe et voyons comment la distinction entre « savoir savant » et « savoir élève » va induire des approches très différentes et une vision radicalement opposée des démarches justificatives.

Sur la figure ci-jointe, P est l’intersection de la bissectrice issue de A et de la médiatrice de [BC], H la projection de P sur (AB) et K la projection de P sur (AC).

Il va de soi que (AHP) est égal à (AKP) et donc AH = AK. De même (PHB) = (PKC) et donc HB = KC. On en déduit alors que AB = AC et que le triangle est isocèle en A.
(Partant, il est d’ailleurs équilatéral…)

Comportement « savant » : Dans le cadre d’un « savoir savant », ce raisonnement est amusant et prend même le statut de démonstration par l’absurde pour justifier que l’un des points H ou K est toujours intérieur au triangle alors que l’autre est extérieur.

Comportement « élève » : Soumise à de jeunes étudiants, cette démonstration entraîne des réactions bien différentes. Pendant plus de 10 minutes, ils cherchent une faille dans le début de la démonstration et remettent en question l’égalité des triangles, puis la correspondance des côtés égaux.

Dans une deuxième phase, c’est la règle du jeu elle-même qui craquelle et finit par céder à travers des remarques comme : « C’est faux car le triangle n’est pas isocèle, un point c’est tout ». Quelques-uns cependant, au bout d’un certain temps, parviennent à s’extraire du cocon de l’élève pour remettre en question la figure.

Si « raisonner juste sur une figure fausse » ne fait pas partie du « savoir élève », le futur professeur reste encore maladroit et n’arrive qu’à proposer de refaire une figure en s’appliquant (d’ailleurs, avec CaRMetal on ne se serait pas trompé).

Redondante dans le cadre d’un « savoir savant », difficilement accessible dans le cadre d’un « savoir élève », ce n’est que dans le cadre d’un « savoir enseignant » qu’une justification s’imposera.

Comportement « enseignant » : On peut par exemple proposer :

Considérons le point P intersection de la bissectrice et du cercle circonscrit au triangle (ABC). Grâce au théorème de l’angle inscrit, le point P est sur la médiatrice de [BC], c’est donc le point construit dans la première partie. Alors, on a plusieurs résultats :

• P est extérieur au triangle (ABC).
• Les angles (AB,BP) et (AC,CP) sont supplémentaires.
• L’un des deux est supérieur à un droit, et l’autre est inférieur à un droit.

Ceci justifie la disposition pressentie des points H et K.

Conclusion

Sur ces exemples colorés, nous avons vu combien la (trans-)formation des enseignants est secouée par d’incessantes « ruptures de contrat ». C’est en m’attachant à mettre en scène ces « ruptures » que j’ai construit le cours de géométrie.

Enfin, cette manière de décrire les différents savoirs permet de relier de façon cohérente les épreuves difficiles des concours au programme plus élémentaire de l’enseignement secondaire.

Accompagner un élève-professeur dans la découverte de son métier est une chose complexe. Nous devons stimuler une mutation du savoir, une prise de responsabilité, un changement de statut en disposant de quelques avantages comme le désir de faire ce métier, la disponibilité et la curiosité et bien sûr de bonnes dispositions dans la discipline.

L’accompagnement sur le terrain est sans doute la tâche la plus délicate du formateur : Il faut arriver à se donner les moyens de porter un regard honnête, critique et constructif tout en limitant au maximum l’effet douloureusement déstabilisant de ce regard lui-même.

Ainsi, j’avais pour habitude, afin de pouvoir communiquer avec mes étudiants lors des activités de terrain de leur demander une fiche décrivant la séquence à laquelle j’allais assister. En comparant leur préparation à leur résultat, nous dégagions les composantes de ce qui pouvait qualifier une « bonne » démarche pédagogique.

Je conviens que cela n’éliminait pas complètement les difficultés, on retrouvait souvent dans la maladresse de la rédaction d’une fiche de préparation les difficultés qui ressortaient dans la séquence, mais cela avait l’avantage de pouvoir être identifié. De plus, réduire la complexité d’un enseignement à une fiche de préparation d’une séquence de trois quarts d’heure avec un objectif à atteindre et une évaluation de son appropriation est caricatural. Il restait que cette fiche représentait un bon catalyseur pour notre travail.

Comment donc inviter mes étudiants à préparer leurs activités de terrain en respectant mes exigences tout en montrant les limites d’une telle préparation ? L’humour me semblant convenir à la situation, voilà une façon originale de mettre en place un tel contrat :

Fiche de préparation

Niveau : 5^e, classe de 25 élèves.

Objectif : « être capable de formuler la loi de l’attraction universelle »

Pré-requis : Latéralisation

Matériel : Un champ de pommiers chargés de fruits, quelques couvertures, 5 gaulette, 5 escabeaux.

Type d’activité : Travaux dirigés en groupes.

Déroulement :

• Former 5 groupes de 5 élèves.
• Étendre les couvertures sous cinq pommiers.
• Demander à 4 élèves de se coucher sur les couvertures au pied des pommiers.
• Le cinquième élève grimpe à l’arbre et fait tomber des pommes sur la tête de ses camarades.
• Échanger les rôles toutes les 5 minutes.
• À chaque changement, le professeur procède à un audit non directif et prend note des remarques des élèves.

De retour en classe, on rédigera dans le cahier de cours : « Deux corps A et B s’attirent avec une force dépendant de leur masses et de leur distance ».

Travail à faire : « Déterminer l’influence de la distance et des masses sur l’attraction universelle. »

Analyse de la séquence : Cela a été une grande réussite. Plusieurs élèves ont su reconnaître et formuler que des pommes étaient tombées sur leur tête. Certains ont eu quelques difficultés, soit qu’ils se soient endormis, soit qu’ils se soient dissipés en mangeant les pommes.

Le travail à la maison a été fait par tous ceux qui ont un ordinateur et qui savent se servir de Google. Quelques erreurs ont été relevées liées souvent à la mauvaise orthographe de Newton dans le moteur de recherche et certains se sont égarés en décrivant les avantages des tondeuses à gazon sans cordon Neuton, ce qui peut-être considéré comme hors sujet.

Nous insistons sur la référence au socle commun de connaissances illustrée par cette dernière remarque : « Ce n’est pas parce que l’on est en cours de sciences que l’on doit négliger l’orthographe ».