A priori, le problème est octodimensionnel, les 8 variables étant les proportions des électeurs des candidats éliminés qui reporteront leurs votes sur François Hollande. Mais en estimant que la quasi-intégralité des voix d’Eva Joly, Jean-Luc Mélenchon, Philippe Poutou, Nathalie Arthaud, Jacques Cheminade et bien entendu François Hollande se reporteront sur François Hollande, et que de même le réservoir de voix de Nicolas Sarkozy s’agrandira de celui de Nicolas Dupont-Aignan, ne subsistent alors que deux inconnues : La proportion x des électeurs de Marine Le Pen qui voteront pour François Hollande au second tour, et la proportion y des électeurs de François Bayrou qui voteront Hollande au second tour.
sans les abstentionnistes
Voici les pourcentages obtenus par les différents candidats, regroupés par affinité :
| Hollande | 28,63 |
| Mélenchon | 11,11 |
| Joly | 2,31 |
| Poutou | 1,15 |
| Arthaud | 0,56 |
| Cheminade | 0,25 |
Soit un minimum de 44,01% minimum pour François Hollande au second tour ;
| Sarkozy | 27,18 |
| Dupont-Aignan | 1,79 |
soit un minimum de 28,97% pour Nicolas Sarkozy.
Marine Le Pen totalise 17,9%, dont x iront à Hollande et 1-x à Sarkozy. Soit 0,179x transférés à Hollande et 0,179(1-x)=0,179-0,179x transférés à Sarkozy.
De même, les 9,13% de Bayrou se répartiront en 0,0913y pour Hollande et 0,0913(1-y)=0,0913-0,0913y pour Sarkozy.
En bref, si les abstentionnistes sont les mêmes au premier tour et au second tour, François Hollande totalisera 0,4401+0,179x+0,0913y des voix, et Nicolas Sarkozy totalisera 0,2897+0,179+0,0913-0,179x-0,0913y=0,56-0,179x-0,0913y des voix. La victoire de François Hollande est caractérisée au choix par l’une des conditions suivantes :
- le premier nombre est supérieur au second (le candidat qui a le plus de voix, gagne) ;
- le premier nombre est supérieur à 0,5 (plus de la moitié des voix, et c’est le tapis rouge à l’Élysée) ;
- le second nombre est inférieur à 0,5 (moins de la moitié des voix, et c’est le congé de paternité).
On peut donc estimer les chances de victoire de François Hollande par l’aire du domaine du plan caractérisée par l’une de ces inégalités ; pour que l’aire soit finie, il faut aussi tenir compte d’autres « contraintes » comme le fait que les variables x et y sont comprises entre 0 et 1.
Pour commencer, on peut déjà dessiner la droite d’équation 0,4401+0,179x+0,0913y=0,5 ce qui, avec GeoGebra, se fait très rapidement, en entrant son équation dans la fenêtre de saisie (en bas de la figure) :
0.4401+0.179*x+0.0913*y=0.5
GeoGebra dessine alors cette droite (en bleu), tout en simplifiant l’affichage de son équation :
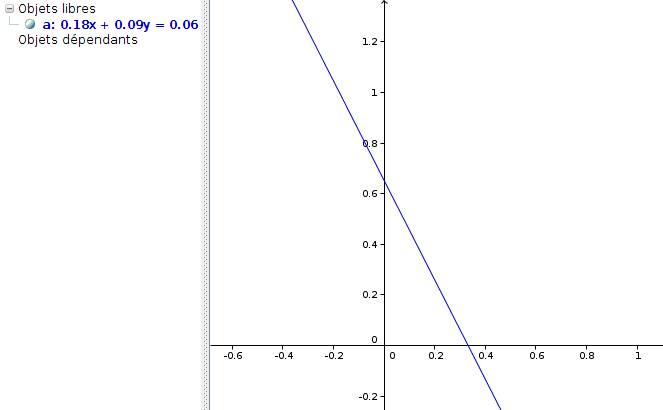
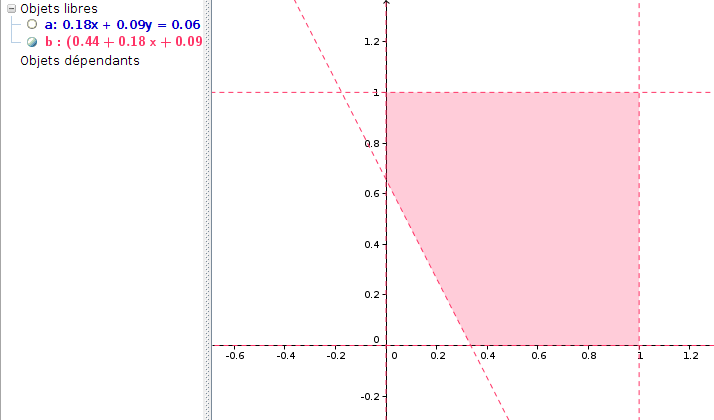
Ce rappel peut être utile en Seconde, surtout pour moi qui n’ai pas encore traité ce chapitre... De surcroît, il prépare à l’étape suivante, qui est la résolution de l’inéquation. Donc si dans la fenêtre de saisie, on entre 0.4401+0.179*x+0.0913*y>0.5, on voit (en rose ci-dessous) un demi-plan :
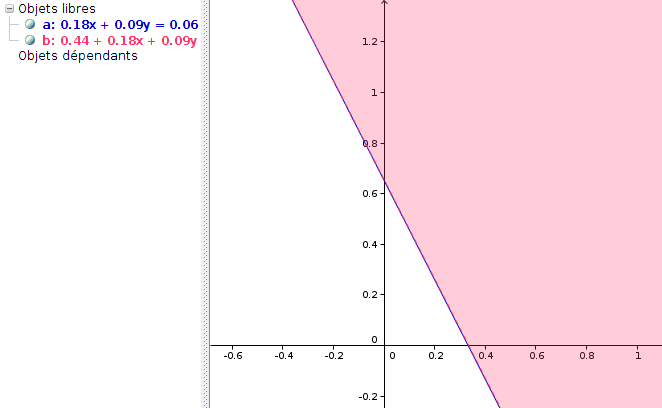
Le domaine dont l’aire est la probabilité de victoire de François Hollande, est l’intersection de ce demi-plan et du carré décrit par 0<x<1 et 0<y<1 ; si on écrit l’encadrement sur x par une double inégalité :
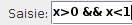
on voit (en vert) une bande dont l’intersection avec l’équivalent pour y est un carré :
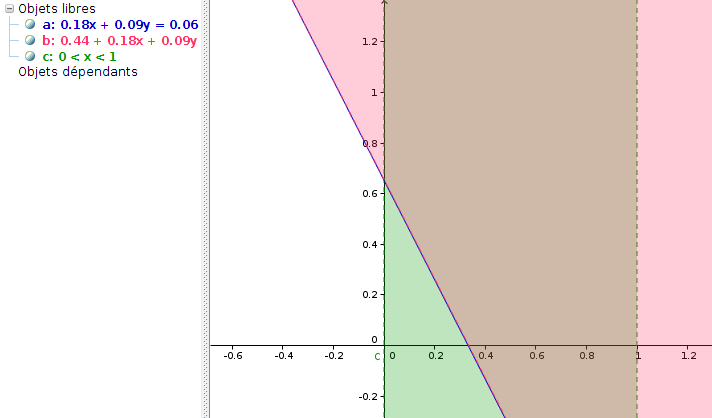
Un bon moyen de mieux y voir est de carrément (!) mettre toutes les inégalités ensemble, séparées par des doubles esperluettes :
On voit alors que l’aire à calculer est celle d’un pentagone :
calcul de la probabilité
Le plus simple pour calculer l’aire du pentagone, est de soustraire à 1 (l’aire du carré) l’aire du triangle donnant la victoire de Nicolas Sarkozy [1] ; pour cela il suffit de connaître les coordonnées des sommets de ce triangle ; on peut les calculer en résolvant les équations 0,179x=0,0599 et 0,0913y=0,0599, ou construire avec GeoGebra les points d’intersection des axes avec la droite bleue :
Il suffit de construire le triangle pour que GeoGebra affiche son aire. Et comme le triangle s’appelle poly1 et que GeoGebra comprend, lorsqu’on utilise le nom poly1 pour un calcul, qu’il s’agit de l’aire, il suffit d’écrire 1-poly1 pour avoir la probabilité :
Avec la précision maximale permise par GeoGebra, on trouve donc une probabilité d’environ 0,890225911263133 de victoire pour François Hollande, soit environ 89% de chances. Soit, en valeur exacte, 2909739 chances sur 3268540 d’être élu.
avec les abstentionnistes
Les abstentionnistes du premier tour ne vont pas nécessairement rester abstentionnistes au second tour, donc si on appelle z la proportion d’entre eux qui votent Hollande au second tour, et 1-z la proportion de ceux qui voteront Sarkozy au second tour, Hollande récupère 0,2053z votes et Sarkozy en récupère 0,2053(1-z)=0,2053-0,2053z, si les 20,53% d’abstentionnistes votent tous au second tour. Cependant, il faut ramener les pourcentages du premier tour, non au total des suffrages exprimés, mais au total des inscrits. Le total devient alors 0,3497+0,1423x+0,0726y pour Hollande et 0,445-0,1423x-0,0726y pour Sarkozy.
Finalement, les voix obtenues par Hollande au second tour deviennent 0,3497+0,1423x+0,0726y+0,2053z dans ce nouveau modèle tridimensionnel, et la probabilité de victoire de François Hollande devient le volume de l’intersection du demi-espace d’équation 0,3497+0,1423x+0,0726y+0,2053z>0,5 avec le cube unité.
Seulement, à l’heure actuelle, GeoGebra 5.0 ne gère pas encore les demi-espaces et leur intersection [2], il va donc falloir construire les sommets du solide un par un, ce qu’on peut aussi bien faire avec CaRMetal [3], et plus précisément à l’aide des fichiers préparés par Jérôme Caré pour la 3D dans CaRMetal, et téléchargeables en bas de l’article.
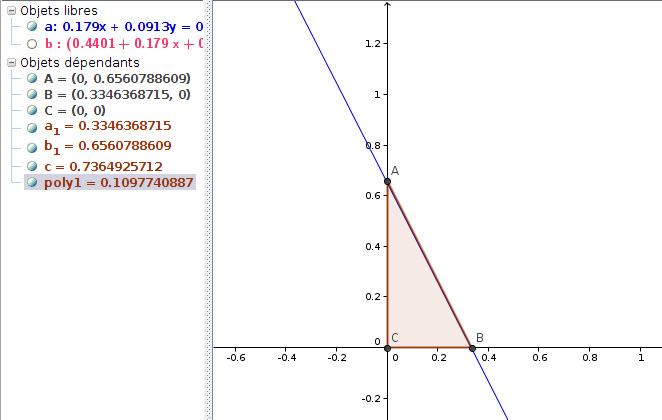
Le plan représentant des scores à égalité pour les deux candidats passe par les points de coordonnées respectives
- (1,0562 ;0 ;0)
- (0 ;2,07 ;0)
- (0 ;0 ;0,732)
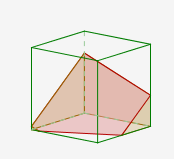
Le script « plan et équation » permet de vérifier que c’est bien le bon plan ; et en rajoutant un cube de centre (0,5 ;0,5 ;0,5) à l’aide de la macro idoine, on n’a plus qu’à construire les points d’intersection pour avoir l’intersection du plan et du cube, qui est là encore un pentagone. La probabilité de victoire de Sarkozy devient maintenant le volume du solide représenté en marron dans la figure ci-dessous :
modèle amélioré
Tout ce qui précède est basé sur l’hypothèse que les variables x, y et éventuellement z suivent une loi uniforme sur [0;1], c’est-à-dire une loi bêta de paramètres 1 et 1 ; rien ne justifie cette hypothèse !
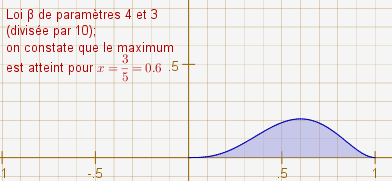
Par exemple, un sondage suggère que 40% des électeurs de Marine Le Pen se reporteraient sur François Hollande au second tour. On peut explorer les lois bêta avec ces curseurs :
Cette exploration montre que le mode d’une de ces lois est le quotient de ses paramètres (à un décalage de 1 près). Donc pour obtenir une loi de mode 0,4, on peut choisir une loi de paramètres 3 et 4, ou 5 et 7, ou 7 et 10, ou 9 et 13 etc.
Par exemple, il semble approprié de modéliser la variable aléatoire x par une loi bêta de paramètres 3 et 4 ; et de même, la loi de y peut être modélisée par une loi bêta de paramètres 2 et 2. Plutôt que de calculer l’aire du domaine pentagonal vu précédemment (c’est-à-dire l’intégrale de la fonction constante 1 sur ce domaine), il serait plus sage d’intégrer le produit des deux lois bêta ci-dessus sur le domaine en question. Ce qui aura sans doute pour effet de diminuer encore la probabilité de victoire de François Hollande.
Mais cette intégrale double dépasse le cadre du programme du lycée...
L’activité de l’onglet 1 est parfaitement faisable en Seconde, grâce à la facilité d’utilisation de GeoGebra 4 ; celle de l’onglet 2 est à la portée de la Terminale S (géométrie repérée dans l’espace) ; celle de l’onglet 3 est hors programme...
Tout ce qu’il faut pour faire de la 3D avec CaRMetal :
Commentaires