« »
Sommaire
- Algorithmes de multiplication
– La multiplication égyptienne
– La multiplication chinoise
– La multiplication per gelosia
– La multiplication avec les doigts - La rabdologie
– Les bâtons de Neper
– Les réglettes de Genaille-Lucas - Les bouliers
– La construction du nombre et de la numération dans les programmes de l’école primaire
– Boulier européen
– L’abaque à tiges
– Le boulier chinois
– Le boulier japonais
– Le boulier russe
– Les bouliers numériques
1. ALGORITHMES DE MULTIPLICATION
De tout temps, l’homme a cherché à produire et utiliser des algorithmes « simples » et efficaces facilitant les calculs. C’est notamment le cas pour la multiplication. Voici quelques-uns de ces procédés manuels. Ils ont en commun l’utilisation minimale, voire nulle des tables de multiplication.
a) La multiplication égyptienne
Il s’agit d’une méthode écrite utilisant uniquement l’addition et la duplication, datant de presque 4 000 ans !
Cette technique est notamment connue grâce au papyrus Rhind écrit au XVIe siècle avant notre ère dans lequel le sage Ahmès expose les connaissances mathématiques de son temps.
Domaine d’application et intérêt : la technique de multiplication en Égypte repose sur la décomposition de l’un des nombres en puissances de deux et la création d’une table de puissance pour l’autre nombre. Elle a l’avantage de ne faire appel qu’à des multiplications par deux ; des soustractions et des additions.
Les Égyptiens de l’antiquité disposent de tables contenant un grand nombre de puissances de deux pour ne pas être obligés de les recalculer à chaque fois.
| $2^0$ | $2^1$ | $2^2$ | $2^3$ | $2^4$ | $2^5$ | $2^6$ | $2^7$ | $2^8$ |
| 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 |
Algorithme : il est constitué de trois étapes.
- Décomposition en puissances de deux de l’un des nombres. Les Égyptiens savent de façon empirique qu’une puissance de deux donnée n’apparaît qu’une seule fois dans un nombre. Pour la décomposition, ils procèdent méthodiquement : ils trouvent d’abord la plus grande puissance de deux inférieure ou égale au nombre en question, la soustraient et recommencent l’opération jusqu’à ce qu’il ne reste plus rien ;
- construction de la table des puissances de deux du second nombre ;
- calcul du résultat : il s’obtient en additionnant tous les nombres de la dernière colonne dont la puissance de deux correspondante fait partie de la décomposition du premier nombre.
Exemple.
On souhaite faire la multiplication de 25$\times$7 . On commence par décomposer le nombre 25 :
– La plus grande puissance de 2 inférieure ou égale à 25 est 16 et 26 - 16 = 9 ;
– la plus grande puissance de 2 inférieure ou égale à 9 est 8 et 9 - 8 = 1 ;
– la plus grande puissance de 2 inférieure ou égale à 1 est 1 et 1 - 1 = rien.
Donc, 25 = 1 + 8 + 16
On a alors :
| ✓ | 1 | 7 |
| 4 | 28 | |
| ✓ | 8 | 56 |
| ✓ | 16 | 112 |
D’où 25$\times$7 = 7 + 56 + 112 = 175.
b) La multiplication chinoise
Il s’agit d’une méthode qui permet de multiplier en utilisant des baguettes. Elle est parfois appelée méthode japonaise.
Domaine d’application et intérêt : c’est une technique graphique dérivée des mathématiques indiennes qui permet de multiplier en dessinant des traits.
Algorithme : il est basé sur le tracé de traits matérialisant les différents chiffres et du dénombrement de leurs points d’intersection.
- On trace verticalement de gauche à droite plusieurs séries de traits correspondant aux chiffres du premier nombre et horizontalement de haut en bas plusieurs séries de lignes correspondant aux chiffres du second nombre ;
- on matérialise le nombre de points d’intersection entre les lignes horizontales et verticales ;
- on additionne ces points sur chacune des « diagonales » en commençant par la diagonale la plus à droite. Les retenues éventuelles sont reportées sur la diagonale suivante. Le résultat de la multiplication se lit de gauche à droite.
Exemple : 123 $\times$ 21 = 2 583

c) Multiplication per gelosia
Il s’agit d’une méthode utilisant un tableau venant de la civilisation indienne au XIIe siècle, puis introduite en Europe par Fibonacci, très utilisée jusqu’au XVe siècle. Le nom per gelosia provient des fenêtres jalousies, sorte de volets à travers lesquelles la lumière passe en diagonale et qui permettent de voir sans être vu.
Cette technique illustre bien la diffusion mondiale de certaines techniques mathématiques puisqu’on la retrouve simultanément à des périodes différentes en Chine, en Inde, dans le monde arabe et en Europe.
Domaine d’application et intérêt : cette méthode permet de multiplier deux nombres quelconques, entiers ou décimaux, écrits dans une base ou un produit n’a jamais plus de deux chiffres. Elle nécessite la connaissance des tables de multiplication, comme notre technique usuelle.
Algorithme : soient x et y deux nombres à multiplier et n et m leurs nombres de chiffres respectifs.
- On commence par dessiner un tableau rectangulaire de n $\times$ m cases carrées ainsi que les diagonales montantes des cases de ce tableau ;
- on inscrit les deux facteurs à l’extérieur du tableau. Si le facteur horizontal est écrit de la gauche vers la droite, alors le facteur vertical est écrit de haut en bas. Si le facteur horizontal est écrit de la droite vers la gauche, alors le facteur vertical est écrit de bas en haut ;
- on inscrit tous les produits dans les cases correspondantes, le chiffre des dizaines étant écrit dans le triangle du haut et le chiffre des unités dans celui du bas ;
- on calcule les sommes à l’intérieur de chaque bande diagonale puis on lit le résultat dans le même sens qu’a été écrit le facteur horizontal.
Exemple : 735 $\times$ 42 = 30 870
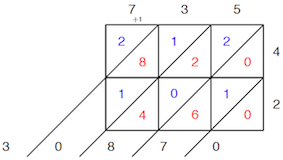
La multiplication par gelosia, bien que très intéressante, présente tout de même quelques défauts : elle est compliquée à « imprimer », elle demande la compréhension du système des retenues, et enfin, la connaissance des tables de multiplication est indispensable.
Exemple d’utilisation hors de l’Europe : en pays d’Islam, plusieurs mathématiciens de langue arabe ont utilisé cette technique dès le VII^e siècle. La figure ci-dessous, correspond à la multiplication 345 $\times$ 437 issue du manuscript de Pamiers.

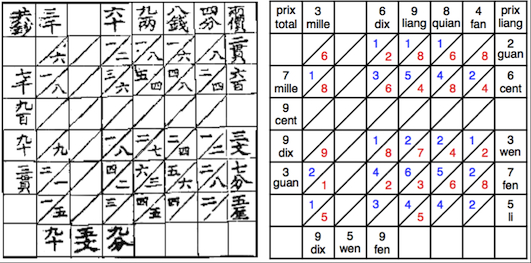
En Chine, l’utilisation du tableau est attestée pour la première fois en 1450. Le tableau ci-dessous est tiré d’un texte de Jiunzhiang suanfa bilei daquan (somme des méthodes de calcul des neuf chapitres comportant des problèmes résolus par analogie avec des problèmes-type) écrit par le gouverneur financier de la province du Zhejiang : Wu Jing.
Soit 3069 liang 8 qian 4 fan de soie. Chaque liang coûte 2 guan 603 wen 7 fen 5 li.
Quel est le prix total ? Réponse : 7993 guan 95 wen 9 fen.
d) Multiplication avec les doigts
C’est une généralisation de la table de multiplication avec les doigts par 9 : il s’agit d’une méthode naturelle qui ne nécessite que ses deux mains et qui permet de calculer un produit dont les deux facteurs sont compris entre 5 et 9 connaissant les tables de multiplication de 1 à 4.
Domaine d’application et intérêt : l’intérêt de cet algorithme est qu’il suffit de connaître la partie plus facile de la table de multiplication où les deux facteurs sont compris entre un et quatre pour trouver les multiplications plus difficiles.
Algorithme : soient x et y les deux entiers compris entre cinq et neuf à multiplier.
- Sur une main, on replie autant de doigts que ce qui dépasse cinq dans x ;
- sur l’autre main, on replie autant de doigts que ce qui dépasse cinq dans y ;
- le nombre de doigts repliés correspond au nombre de dizaines du produit, auquel on ajoute le produit des doigts levée sur chacune des deux mains.
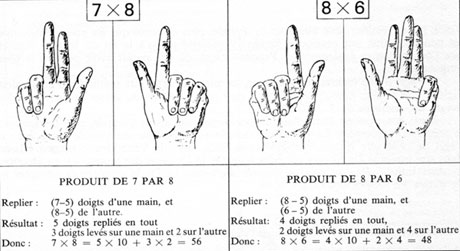 Multiplication avec les doigts
Multiplication avec les doigts
Justification :
- le nombre x est représenté sur une main par x - 5 doigts repliés et 10 - x doigts levés ;
- le nombre y est représenté sur l’autre main par y - 5 doigts repliés et 10 - y doigts levés.
- Calcul des dizaines : d = (x - 5) + (y - 5) = x + y - 10 ;
- calcul des unités : u = (10 - x)(10 - y) = 100 - 10(x + y) + xy.
- Calcul du produit : 10d + u = 10(x + y - 10) + 100 - 10(x + y) + xy
= 10x + 10y - 100 + 100 - 10x - 10y + xy = xy.




Commentaires