L’orthogone de Lill, un algorithme qui allie algèbre et géométrie

Construction géométrique des solutions d’une équation du second degré
mercredi 6 octobre 2010
par  Nathalie CARRIÉ

Je viens de proposer à mes premières S une construction géométrique des solutions d’une équation du second degré.

Cette construction nous vient d’un capitaine du génie de l’armée autrichienne, Eduard Lill, qui publie en 1867 une construction des solutions d’une équation polynomiale de degré n. [1].

Je me suis inspirée d’un TP proposé par l’IREM de Strasbourg [2] dont voici l’énoncé :

Orthogone de Lill : TP de l’IREM de Strasbourg

La résolution graphique à l’aide de l’orthogone de Lill

Dans le repère orthonormé $(O, \vec{i}, \vec{j}) $, les points de la figure ont pour coordonnées :

$ A(1+a ; 0) $ $ B(0 ; b) $ $ C(1+a-c ; b) $ et $ P(0 ; \alpha) $

Coordonnées du point M

Le point M a pour coordonnées : $ M(1+a ;y_M) $ .
La droite (IP) a pour équation $ y = - \alpha x + \alpha $.
On calcule $y_M$ en écrivant que M appartient à la droite (IP).
Le point M a donc pour coordonnées : $ M(1+a ; - \alpha a )$

Coordonnées du point N
On exprime que la droite (MN) est perpendiculaire à (IP), puis que N a pour ordonnée b.

On trouve finalement que N a pour coordonnées $ N(1+\alpha^2 a + \alpha b + a ; b ) $

Lorsque N est en C, il suffit alors d’exprimer que les coordonnées de C et de N sont égales :

N est en C $ \Leftrightarrow 1+\alpha^2 a + \alpha b + a = 1+a - c $
d’où
N est en C $ \Leftrightarrow \alpha^2 a + \alpha b + c = 0 $,
c’est à dire si
$\alpha $ est solution de l’équation $ ax ^2+bx+c=0 $.

Construction
Quand N est en C, le triangle IMC est rectangle en M et donc le point M appartient au cercle C de diamètre [IC].

Conclusion
Le cercle C de diamètre [IC] coupe la droite (AB) en au plus deux points. Si M est l’un de ces points, la droite (IM) coupe l’axe des ordonnées en un point dont l’ordonnée est solution.

OrthogoneDeLillExemple1

Le détail manuscrit des calculs faits en classe se trouve dans les images du portfolio (pages écrites avec le logiciel Xournal). [3]

On peut retrouver algébriquement la condition d’existence des solutions en écrivant que le cercle C de diamètre [IC] coupe la droite (AB) si et seulement si $d(\Omega, (AB))<= \frac{IC} { 2} $. Le détail du calcul se trouve ici.

Le calcul classique des solutions de l’équation du second degré

Le script de base de résolution d’une équation du second degré

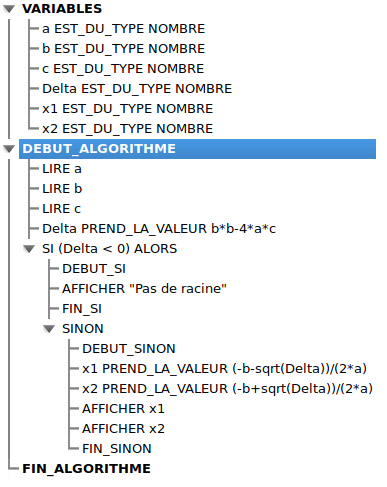
L’algorithme

AlgorithmeDuSecondDegre

En javascript avec CarMetal

20100917 ProgrammeSecondDegreEnJavascript

Avec Scratch

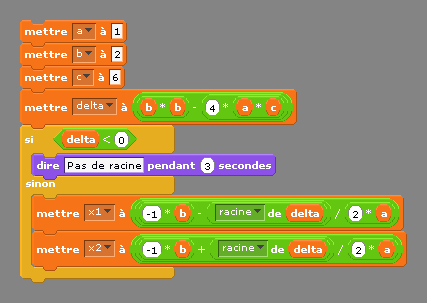
AlgorithmeSecondDegreScratch

Avec AlgoBox

AlgorithmeDuSecondDegreAlgoBox

Avec la calculatrice TI-82

AlgorithmeDuSecondDegreTI82

Ce code calculatrice peut être entré et testé sur la page TI-Editor de Texas Instrument.

L’interaction des deux dans une figure CarMetal

Faire un script javascript dans CarMetal pour afficher dans une console les solutions ne présente aucun avantage par rapport à l’utilisation de la TI-82 ou d’un autre logiciel de programmation. Par contre, si le calcul du script interagit avec la figure, cela devient nettement plus intéressant, surtout dans ce cas précis : la construction de l’orthogone de Lill fournit une construction des solutions et donc une lecture approchée des racines ; le script vient en complément confirmer cette lecture.

L’orthogone de Lill en CaRMetal

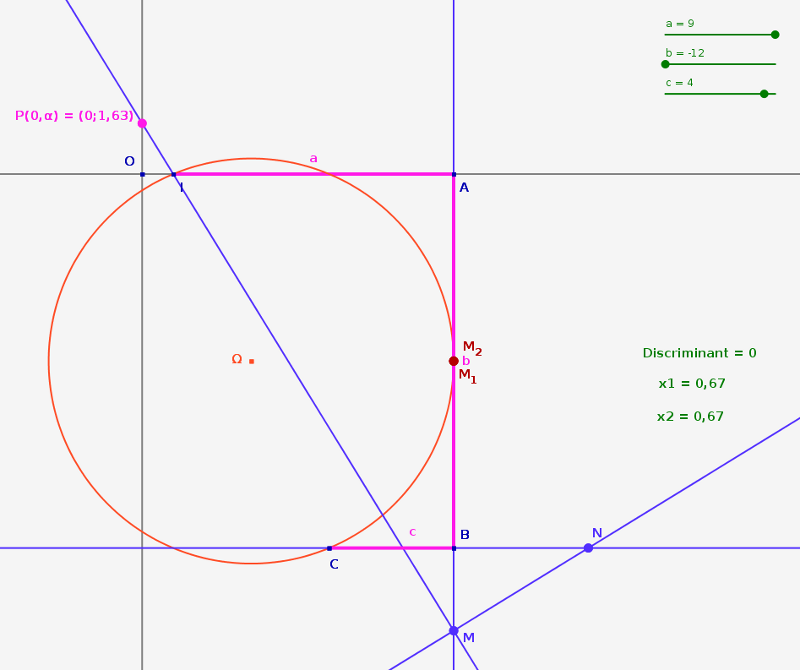
Cette figure est manipulable. Vous pouvez bouger les curseurs et le point P.

Manipulation de la figure :

– Modifier les valeurs de a, b et c à l’aide des curseurs prévus à cet effet.
– Lancer le script SecondDegre. Il fournit le calcul des racines.
– On peut retrouver géométriquement le résultat du calcul algébrique :

OrthogoneDeLillAlgorithmeGeometrique


– Les exemples de l’énoncé.

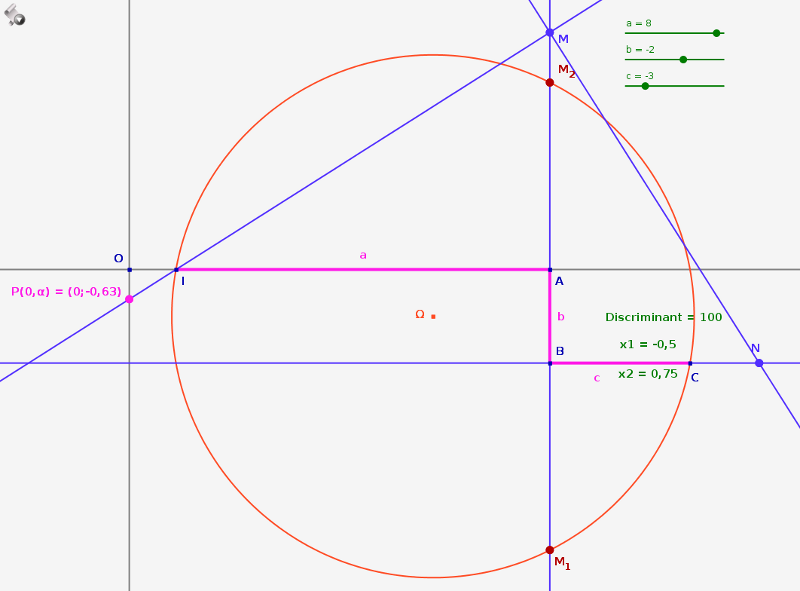
  1. $a=8$ , $b=-2$ , $c= -3$
    Le cercle de diamètre [IC] coupe la droite (AB) en deux points. L’équation $8x^2-2x-3=0$ a donc deux solutions.
    OrthogoneDeLillDeuxRacines
  2. $a=3$ , $b=-4$ , $c= 2$
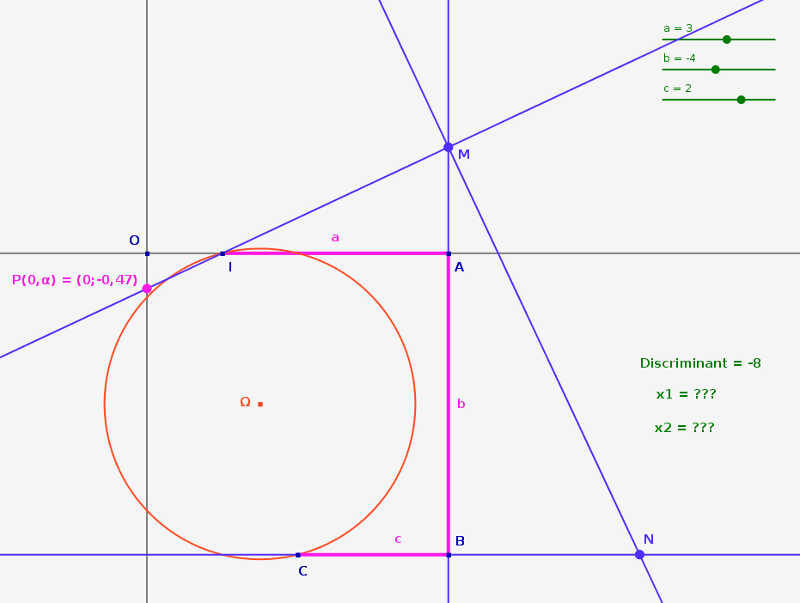
    Le cercle de diamètre [IC] ne coupe pas la droite (AB). L’équation $3x^2-4x+2=0$ n’a donc pas de solution.
    OrthogoneDeLillPasDeRacine
  3. $a=9$ , $b=-12$ , $c= 4$
    Le cercle de diamètre [IC] est tangent à la droite (AB). L’équation $9x^2-12x+4=0$ a donc une racine double.
    OrthogoneDeLillRacineDouble

Détails sur les scripts :

Les scripts se rentrent via le menu Javascript -> Ouvrir l’éditeur de script.
Cette figure contient deux scripts :

– le script SecondDegre ci-dessous :

SecondDegreParCurseurs

Il permet de modifier les valeurs des coefficients a, b et c par les curseurs. Il renvoie alors les solutions, lorsqu’elles existent.

– le script Fixerabc ci-dessous :

SecondDegreParSaisie

Il permet de fixer les valeurs de a, b et c en les entrant au clavier.


[1] « Du compas aux intégraphes : Les instruments du calcul graphique », Dominique Tournès, Irem de La Réunion et Equipe REHSEIS, REPERES - IREM. N° 50 - janvier 2003

[2] Math Premières Scientifiques, IREM de Strasbourg, collection ISTRA, 1988

[3] L’ensemble des pages manuscrites en classe devant les élèves se trouvent sur le site Maths en classe en images.


Portfolio

20101008 OrthogoneDeLill1 20101008 OrthogoneDeLill2 20101020 OrthogoneDeLillConditionDexistenceDesSolu OrthogoneDeLillDeuxRacinesb OrthogoneDeLillExemple1 M1 OrthogoneDeLillExemple1 M2

Commentaires

Logo de Marc JAMBON
vendredi 12 novembre 2010 à 16h46 - par  Marc JAMBON

Le cas b = 0 est parfaitement traité par cette méthode pourvu qu’on parle de la perpendiculaire par A au premier axe et non de la droite (AB) qui n’est pas définie pour b = 0. L’exploitation complète de la méthode devrait conduire aussi à l’étude de la position relative du cercle de diamètre [IC] et de cette droite perpendiculaire par A au premier axe, on retrouve bien entendu (si on n’a pas fait d’erreur de calcul) la discussion classique. On note en particulier que lorsque le cercle est un cercle-point, ce point est hors de la droite, donc aucune solution et la difficulté disparaît d’elle-même.

Logo de Nathalie Carrié
mardi 9 novembre 2010 à 07h57 - par  Nathalie Carrié

1. Il va de soi que a est non-nul puisque la méthode vise à résoudre des équations du second degré.
2. Effectivement, le cas b=0 n’est pas géré ici. Merci de l’avoir signalé.
3. L’abscisse du point N est rectifiée dans l’article.

Je vous remercie pour votre remarque.

Logo de Marc jambon
vendredi 5 novembre 2010 à 11h55 - par  Marc jambon

Quand on parle d’une droite définie par deux points en géométrie, on devrait toujours s’assurer au préalable que les deux points sont distincts.
Ici, il n’y a pas de problème pour I et P toujours distincts donc OK pour la droite (IP) ; ce n’est pas évident pour la droite (IM), il y a lieu à une dicussion qui peut être simplifiée en supposant a ≠ 0 dès le départ de façon à partir d’une vraie équation degré ; pour la droite (AB) , A et B peuvent être confondus, on gagnerait à parler de la perpendiculaire par A à la droite (OI) ou au premier axe de coordonnées.

De même quand on parle d’un cercle de diamètre défini par deux points on devrait toujours s’assurer que ces deux points sont distincts, sinon on tombe sur un cercle-point et certaines propriétés peuvent être en défaut. Ici, concernant le cercle de diamètre [IC], il y a bien un probléme car les points I et C peuvent être confondus, le cercle de diamètre [IC] serait alors un cercle-point qui ne garantit pas que le triangle IMC soit un vrai triangle (trois sommets alignés ou peut-être confondus) et encore moins qu’il est rectangle en M. 

Je signale aussi une faute de calcul (ou de frappe)
L’abscisse de N est 1 + α^2 + αb + a et non α^2 + αb + a.