C’est dans un article de janvier 1973 (dans scientific american) que Martin Gardner présentait le jeu suivant, qu’il a baptisé chomp pour suggérer l’idée de croquer dans les biscuits (cliquer dessus pour jouer en ligne) :

En fait, le jeu a été inventé par David Gale [1] sous le nom de « une curieuse variante du jeu de Nim » :

C’est une variante de Nim parce que, au lieu de mettre les pièces en tas, on les dispose en rectangle avec la règle selon laquelle chaque fois qu’on ramasse une pièce, on ramasse aussi celles qui sont à sa droite et au-dessous d’elle (compris), alors qu’à Nim, lorsqu’on ramasse une pièce, on ramasse aussi celles qui sont au-dessus d’elle dans le tas de pièces.

En mai 1973, Martin Gardner explique qu’en fait le jeu de Chomp existait déjà en 1952 avec un article de Fred Schuh titré Spel van delers et portant sur un jeu dit de division :

On part d’un nombre entier strictement supérieur à 1 ; chaque joueur à son tour choisit un diviseur du nombre courant, dont aucun multiple n’a déjà été choisi au cours du jeu. Le premier joueur qui ne peut jouer que 1, perd.

En fait, Chomp (jeu) est un cas particulier du jeu de la division, lorsque le nombre de départ n’a que deux facteurs premiers comme 2 et 3 :

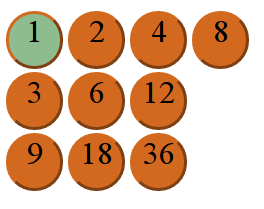
Chaque biscuit porte le double du biscuit à sa gauche et le triple de celui de dessus. On a ainsi un tableau des diviseurs de 576, placés de manière que les multiples de l’un de ces diviseurs se trouvent à sa droite et en-dessous. On a donc bien un jeu analogue à celui de la soustraction, mais où on effectue des divisions successives au lieu de soustractions. Ce jeu, surtout dans sa version « calcul mental », est donc un jeu sérieux sur la divisibilité (savoir reconnaître un multiple du nombre joué à l’instant).

Stratégie gagnante

En inventant Chomp, Gale a prouvé l’existence, pour le premier joueur, d’une stratégie gagnante. Mais sa preuve est non constructive, puisqu’elle ne permet pas de trouver comment gagner :

On raisonne par cas, en se concentrant sur le coup consistant à enlever en premier le biscuit tout en haut à droite :

• ou bien ce coup est gagnant pour le premier joueur, et dans ce cas il existe une stratégie gagnante, qui commence par « enlever le biscuit en haut à droite » (exemple ci-dessous) ;
• ou bien ce coup est perdant pour le premier joueur, ce qui signifie que le second joueur peut enlever un autre biscuit en guise de coup gagnant. Mais dans ce cas, le premier joueur aussi pouvait arriver directement à cette position gagnante, dès le premier coup. Dans ce cas aussi, il existe une stratégie gagnante pour le premier joueur.

Le problème est qu’on ne peut pas savoir d’avance si on est dans le premier cas ou le second. Du moins, pas facilement. Pour le Chomp 3×2 on peut faire le graphe du jeu :

Et on peut y jouer comme aux jeux de Nim avec pion, en déplaçant alternativement (chaque joueur à son tour) un unique pion sur ce graphe. En faisant comme les élèves de la fête de la science et de la semaine des maths, on peut marquer (ici en noir) les cases « gagnantes », c’est-à-dire celles où veut aller chaque joueur pour gagner :

Ceci permet de verbaliser la stratégie gagnante pour le premier joueur :

• enlever le biscuit tout en haut à droite (dans le jeu 3×2 c’est un coup gagnant) ;
  • si l’adversaire n’enlève qu’un biscuit, jouer ce qu’il faut pour qu’il ne reste que 3 biscuits non alignés (case au milieu tout à droite du graphe)
  • sinon il ne reste plus qu’une ligne de biscuits ; les manger tous sauf celui qui est empoisonné

Le problème pour généraliser cette stratégie est de nature combinatoire : Le graphe devient vite tellement compliqué qu’il est concrètement impossible de trouver la stratégie gagnante par coloration du graphe. Il est d’ailleurs même difficile de dessiner le graphe !

Le successeur de Martin Gardner dans scientific american, Ian Stewart, a publié en 1996 un article sur une généralisation du jeu de Fred Schuh, qu’il a baptisée « diviser ou multiplier pour régner » mais aussi « juniper green », du nom de l’école où travaillait l’auteur du jeu (le fils d’un collègue de Stewart), un certain Richard Porteous, dont Stewart dit qu’il a inventé le jeu vers 1985. Voici la description de Juniper Green (jeu) par Julien Pavageau :

Le jeu se joue à deux, avec un plateau composé des 25, 50 ou 100 premiers nombres entiers et selon les règles suivantes :

• le premier joueur coche un nombre.
• chaque joueur coche un nombre parmi les multiples ou les diviseurs du nombre choisi par son adversaire au coup précédent.
• un joueur est déclaré gagnant si son adversaire ne peut plus jouer.

Noter que dans l’article de Stewart (dans scientific american), on remplace les biscuits numérotés par des cartes portant les entiers successifs :

Deux différences par rapport à Chomp :

1. On peut aussi choisir un multiple du nombre précédent (et pas seulement un diviseur) ;
2. On peut jouer un multiple d’un nombre précédemment joué, du moment que ce multiple n’a pas déjà été joué auparavant (carte retournée dans le dessin ci-dessus).

Juniper Green n’en est pas moins un jeu sur la divisibilité. On peut aussi s’y intéresser en algorithmique. Voici la description du jeu dans le manuel sésamath 3^e :

Le jeu de Juniper Green a même été donné en BTS SIO :

Cela a donné à Boris Laval et Olivier Sicard l’envie de développer une IA pour ce jeu, IA qu’ils ont présentée ici.

Le « jeu de Nim à un seul tas » est appelé par Berlekamp, Conway et Guy « jeu de soustraction » : On a un tas de pièces, et chaque joueur à son tour enlève un certain nombre de pièces de ce tas, pourvu que ce nombre appartienne à un ensemble fixe :

• Dans le jeu « de Fort Boyard », l’ensemble est formé des nombres 1, 2 et 3

  

   ;

• Dans la variante « soustrais un carré », l’ensemble est formé des carrés parfaits

  

  .

Conway et al proposent alors une variante appelée « dim^- » (mélange de « diviseur » et « nim »), où le nombre de pièces prélevées du tas est un diviseur du nombre actuel de pièces. Ce jeu est gagnant pour le premier joueur, puisque n étant divisible par n, il suffit d’enlever toutes les pièces d’un coup ! Deux variantes peuvent alors rendre le jeu plus intéressant :

• « qui perd gagne » ( on dit aussi « misère »), où le but de jeu est de ne pas être celui qui vide le tas ;
• restreindre les coups possibles aux diviseurs propres (ou « parties aliquotes ») de n, c’est-à-dire n exclu.

Le jeu des parties aliquotes combine ces deux choix. Il a été publié en octobre 1970 par David L. Silverman dans le Journal of Recreational Mathematics.

Ce jeu a déjà été présenté sur ce site et on peut y jouer en ligne, en mode « plateau » [3] :

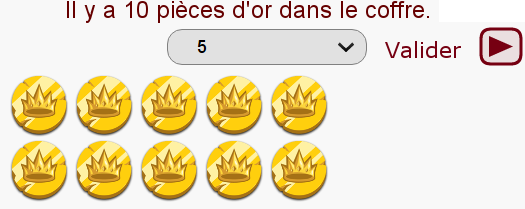
Mais, à la thématique des biscuits dont le dernier est moisi, a été préférée ici celle des pièces d’or dont la dernière est maudite. Ce qui permet deux améliorations du plateau de jeu :

1. dessiner les pièces disposées en rectangle pour rendre visible la divisibilité du nombre total par le nombre choisi ;
2. proposer un choix parmi les diviseurs propres, sous forme d’un menu déroulant.

Avec ces améliorations, le jeu se prête à une implémentation sur tablette tactile, et même sur DGPad. Les lecteurs munis de tablette peuvent tenter la connexion avec ce code :

Voici d’ailleurs le fichier DGPad pour ceux qui préfèrent jouer en local [4] :

Cela donne envie de développer des jeux sur DGPad [5] ! Un aspect intéressant de cette version du jeu est le changement automatique d’avatar selon le joueur dont c’est le tour. Les deux joueurs s’appellent respectivement Barberousse et Jabuse, et voici leurs avatars respectifs :

Barberousse	Jabuse

Quand c’est au tour de Jabuse de jouer, on voit le visage de Jabuse, et quand c’est au tour de Barberousse de jouer, on voit le visage de Barberousse. De cette manière, on joue de la façon suivante :

• Le joueur « Barberousse » commence, en prenant la tablette et en choisissant parmi les diviseurs du menu, celui qu’il veut jouer. Une fois ce choix effectué, il valide puis passe la tablette à l’autre joueur ;
• La tablette indique que c’est au tour de Jabuse de jouer, il choisit donc un diviseur à l’aide du menu déroulant puis passe la tablette à Barberousse ;
• retour au premier point, jusqu’à ce que l’un des joueurs ait perdu, ce qui s’annonce par un message d’alerte modal (il empêche de continuer à jouer).

C’est ce qu’on entend par « mode plateau ». Pour pratiquer ce jeu en classe, il faut donc placer les élèves à deux par tablette, ce qui nécessite donc une douzaine de tablettes en classe entière. Par la suite, on peut faire d’autres séances du jeu sans tablette, lors de séances de calcul mental.

La pratique de ce jeu sérieux amène rapidement à faire des constatations concernant la divisibilité :

1. 1 est toujours présent dans la liste des diviseurs d’un nombre : Tout entier supérieur à 1 est divisible par 1.
2. Certains nombres n’ont pas d’autres parties aliquotes : Ce sont les nombres premiers.
3. On ne change pas la divisibilité par un nombre en soustrayant ce nombre. Par exemple, en soustrayant 13 à 65, on obtient encore un multiple de 13.
4. Un nombre impair n’a que des diviseurs impairs.
5. On change la parité d’un nombre en lui soustrayant un nombre impair ; on conserve la parité d’un nombre en lui soustrayant un nombre pair.

Ces remarques peuvent mener à la découverte de l’algorithme d’Euclide ; ce jeu est un entraînement aux critères de divisibilité, et enfin, il possède une stratégie gagnante très simple, basée sur la notion de parité, c’est-à-dire, de divisibilité par 2.

Pour finir, voici la version Android du jeu des parties aliquotes pirates, à utiliser sur un smartphone ou une tablette pour deux joueurs (en mode avion de préférence). Il faut décompresser le fichier zip pour récupérer un fichier apk qui fait tout seul l’installation Android :

Ce jeu a été créé lors de la rédaction de cet article (comme exemple de variable aléatoire en 1^re).

Il se joue à plusieurs joueurs (pas nécessairement 2) avec un dé (de préférence icosaédrique). Chaque joueur à son tour lance le dé, puis compte (sous vérification des autres joueurs) les diviseurs du résultat affiché par le dé, et marque autant de points que le résultat du dé a de diviseurs. Par exemple si le dé tombe sur 9 (dont les diviseurs sont 1, 3 et 9) le joueur marque 3 points car 9 a 3 diviseurs.

On lance le dé plusieurs (par exemple 8) fois et chaque joueur accumule les points obtenus ainsi. Le joueur ayant obtenu le plus grand total à l’issue des 8 lancers de dés est le gagnant du jeu. En cas d’ex-aequo les joueurs ayant le plus de points continuent seuls à jouer jusqu’à ce que le sort les départage.

Outre la pratique de l’addition pour compter les points et la vérification mentale des diviseurs d’un nombre, la pratique de ce jeu amène à ceci :

• Compter les diviseurs de 8 se fait de plus en plus vite, avec l’expérience : au début on vérifie (mentalement) que 3 n’est pas un diviseur de 8, après on finit par retenir suite aux calculs précédents, que les diviseurs de 8 sont 1, 2, 4 et 8 et qu’il y en a donc 4.
• À la longue on finit même par retenir le nombre de diviseurs de chacun des entiers entre 1 et 20.
• Les nombres 2, 3, 5, 7, 11, 13, 17 et 19 ressortent du lot car chacun d’entre eux ne rapporte que 2 points. Ce sont les nombres premiers que l’on découvre ainsi par le jeu.
• La situation la pire est lorsque le dé tombe sur 1 qui n’a qu’un seul diviseur : cela habitue les enfants dès le cycle 3 à l’idée que 1 n’est pas un nombre premier.

Voici la présentation du jeu avec la liste des items du programme de cycle 4 concernés :

Mais dès le cycle 3 ce jeu peut être source de joie et d’apprentissage simultanés !