Algorithmes, simulations et échantillonnage

jeudi 11 février 2010
par  Nathalie CARRIÉ

Les préconisations du Bulletin officiel n° 30 du 23 juillet 2009 dans le cadre des probabilités et statistiques sont les suivantes :

EchantillonageIndicationsDuBO

En voici les contenus, capacités attendues et commentaires :

EchantillonageIndicationsDuBOb

Cet article propose en conséquence quelques exemples d’algorithmes utilisables pour réaliser des simulations avec les élèves en classe de seconde, en vue d’en exploiter les résultats pour échantillonnages. Ces algorithmes sont mis en œuvre soit sur tableur, soit sur calculatrice, soit les deux et enfin avec le logiciel Scratch.

Simulations de naissances

Simulation sur un tableur

SimulationNaissances1

Nous allons apprendre dans cette fiche cinq nouvelles fonctions de tableur utiles aux simulations.
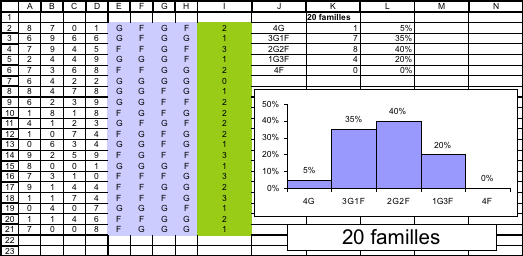
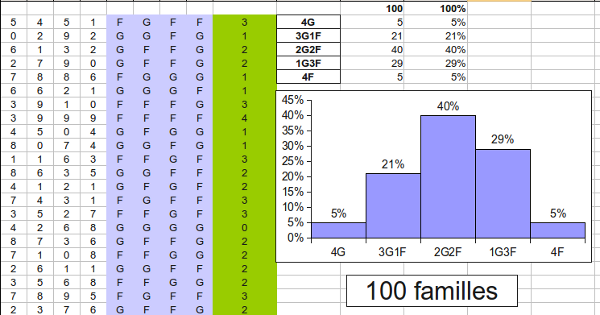
Le but de cette fiche est de reproduire la feuille de tableur ci-dessus dans laquelle on a simulé 20 familles de 4 enfants, à l’aide de nombres aléatoires (cellules A2 à D21).

Le codage choisi est le suivant : Pair= Garçon, Impair= Fille.

Simulations20familles1
Simulations20familles2

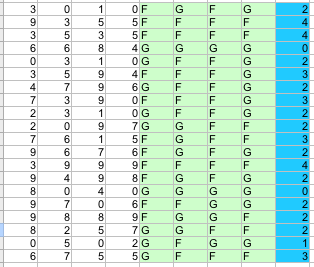
Les commandes de tableur dont nous avons besoin :
Les fonctions Alea() et Ent(), les fonctions Si() et Mod() et pour le comptage, la fonction Nb.Si().

Les fonctions Alea() et Ent()

Tirage d’un nombre aléatoire entier :

Alea( ) tire un nombre aléatoire (réel) entre 0 et 1 (1 exclu).
Ent( ) prend la partie entière d’un nombre réel.
Ainsi, pour tirer un nombre aléatoire entier compris entre 0 et 9, il faut faire Ent(10*Alea()).

Les nombres contenus dans la plage A2:D21 sont donc donnés par :
Ent(10*Alea()) .

Codage : les fonctions Si() et Mod()

La fonction Si( ) permet de tester une condition. Elle est très puissante et très utilisée en programmation.

Si

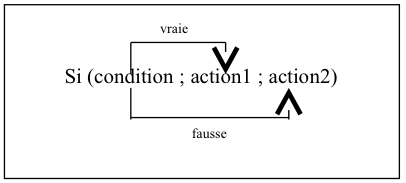
Ainsi la fonction Si teste la condition. Si elle est vraie, le tableur réalise l’action 1. Sinon, c’est l’action 2 qui est exécutée.

A l’aide de cette fonction Si, le codage du nombre aléatoire tiré dans la cellule A2 est par exemple :
Si( A2=2 ; « G » ; « F »)
(Si le contenu de la cellule A2 est un 2, inscrire un G, sinon inscrire un F.)
Mais le test réel que nous devons effectuer est : si le nombre est pair, inscrire un G sinon, inscrire un F. Nous devons donc tester si un nombre est pair.

La fonction Mod( ) renvoie le reste d’une division euclidienne :
Mod(25 ; 10) vaut 5 puisque c’est le reste de la division de 25 par 10.

Mod(A2 ; 2) renvoie le reste de la division du contenu de la cellule A2 par 2.
Si le reste est 0, le nombre est pair, sinon, il est impair.
D’où le test nécessaire pour coder le contenu de la cellule A2 en E2 :

Mod

Comptage : la fonction Nb.Si()

La fonction Nb.Si( ) permet de compter :
Nb.Si(plage ; critère) compte le nombre de fois que le critère est rencontré dans la plage indiquée.

En I2, on compte le nombre de F dans une famille. La formule de la cellule I2 est donc :
Nb.Si(E2 : H2 ; « F »)

Exercice

Donner les formules des cellules D11, E16, I10, K2 à K6 puis L2 à L6.
Finir la feuille en reproduisant l’histogramme.

Conclusion

Lorsque la feuille de tableur est terminée, appuyer sur la touche F9 dix fois et noter les résultats des 10 simulations (cases J2 à L6).
Représenter sur un graphique une des valeurs observées pendant les 10 simulations (par exemple la fréquence des familles de 3G1F).
Quelle conclusion peut-on en tirer ?

Suivre le paramètre 3G1F. Noter les valeurs observées. Comparer à la valeur théorique.
Donner pour 100 et pour 1000 simulations les résultats obtenus dans un tableau. (On appuiera pour cela autant de fois que nécessaire sur la touche F9).
Quelle conclusion peut-on en tirer ?

Simulations 100 familles

Simulations de promenades aléatoires

Citons le document ressource pour la seconde Probabilités et statistiques.

Marche aléatoire

Promenades aléatoires sur une droite

Promenades à 4 pas

On simule à la calculatrice 100 promenades à 4 pas. Pour chaque simulation, on dénombre le nombre de promenades qui se terminent à la distance 0, 2 ou 4 de l’origine. On effectue 10 simulations de ce genre.

Tableau Promenades à 4 pas

Pour 1000 promenades, combien de promenades se terminent à la distance 0 du point de départ ? à la distance 2 ? à la distance 4 ? Calculer la distance moyenne du point de départ au bout de ces 1000 promenades. Comparer avec la distance moyenne théorique (1,5).

Promenades à 5 pas

On simule à la calculatrice 100 promenades à 5 pas. Pour chaque simulation, on dénombre le nombre de promenades qui se terminent à la distance 1, 3 ou 5 de l’origine. On effectue 10 simulations de ce genre.

Tableau Promenades à 5 pas

Pour 1000 promenades, combien de promenades se terminent à la distance 1 du point de départ ? à la distance 3 ? à la distance 5 ? Calculer la distance moyenne du point de départ au bout de ces 1000 promenades. Comparer avec la distance moyenne théorique (1,875).

Les programmes TI89 ou TI92

Promenade à n pas

A l’aide du programme suivant, on pourra remplir les tableaux.

Programme promalea()

() Prgm 
Local a,dist,npas,npasd,npasg 
ClrIO 
Disp " promenade a npas : " 
Prompt npas 
For i,1,npas 
int(2*rand()+1)-1→a[i] 
EndFor 
Disp a 
0→dist:0→npasd:0→npasg 
For i,1,npas 
If a[i]=1 Then 
npasd+1→npasd 
Else
npasg+1→npasg 
EndIf 
EndFor 
If npasd=npas or npasg=npas Then 
npas→dist
Else 
npasd-npasg→dist 
EndIf 
Disp " distance de l origine " 
Disp abs(dist) 
EndPrgm

100 Promenades à 4 pas

Programme prom4()

() Prgm 
Local a,dist 
ClrIO 
Disp " 100 promenades " 
For j,1,100 
0→dist[j] 
For i,1,4 
int(2*rand()+1)-1→a[i] 
EndFor
Disp a 
If a[1]=0 and a[2]=0 and a[3]=0 and a[4]=0 or a[1]=1 and a[2]=1 and a[3]=1 and a[4]=1 Then 
4→dist[j] 
Else 
For i,1,4 
If a[i]=0 Then 
dist[j]-1→dist[j] 
Else 
dist[j]+1→dist[j] 
EndIf 
EndFor 
EndIf 
EndFor 
0→n0 : 0→n2 : 0→n4 
For j,1,100 
If dist[j]=0 Then 
n0+1→n0 
ElseIf abs(dist[j])=2 Then 
n2+1→n2 
ElseIf abs(dist[j])=4 Then 
n4+1→n4
EndIf 
EndFor 
Disp " distance = 0 ",n0 
Disp " distance = 2 ",n2 
Disp " distance = 4 ",n4 
EndPrgm

100 Promenades à 5 pas

Programme prom5()

() Prgm 
Local a,dist,npas,npasd,npasg 
ClrIO 
Disp " 100 promenade a npas : " 
Prompt npas 
For j,1,100 
0→dist[j]:0→npasg:0→npasd 
For i,1,npas 
int(2*rand()+1)-1→a[i] 
EndFor 
Disp a 
For i,1,npas 
If a[i]=1 Then 
npasd+1→npasd 
Else 
npasg+1→npasg 
EndIf 
EndFor 
If npasd=npas or npasg=npas Then 
npas→dist[j] 
Else 
npasd-npasg→dist[j] 
EndIf 
Disp " distance de l origine " 
Disp abs(dist[j]) 
EndFor
0→n1:0→n3:0→n5 
For j,1,100 
If dist[j]=1 Then 
n1+1→n1
ElseIf abs(dist[j])=3 Then 
n3+1→n3 
Else 
n5+1→n5
EndIf 
EndFor 
Disp " distance = 1 ",n1 
Disp " distance = 3 ",n3 
Disp " distance = 5 ",n5 
EndPrgm

Promenades aléatoires sur un triangle équilatéral

ABC est un triangle équilatéral . On définit un sens de parcours direct sur ce triangle : A → B → C → A . Le sens indirect est alors : A → C → B → A. Une puce se déplace sur les bords de ce triangle en sautant d’un sommet à l’autre. Toutes les secondes, la puce change de sommet en choisissant son sens de parcours de manière aléatoire. Ainsi, si la puce est en A, elle peut sauter en B ou en C. Elle part de A au temps 0 et sa promenade dure 4 secondes.

La puce voudrait connaître son nombre moyen de passages par le point A au bout d’un grand nombre de promenades.

Exemples de promenades :
BCBA : 1 passage en A
BABA : 2 passages en A
CBCB : 0 passage en A

Codage et simulation

a. Expliquer comment simuler une promenade avec :
– une pièce de monnaie
– un dé
– une table binaire de 0 et de 1

b. Simuler 20 promenades à l’aide de la table binaire de nombres aléatoires fournie. On choisira son premier nombre en piquant sur la feuille au hasard et on écrira sur sa copie la suite de nombres aléatoires obtenue, puis son codage.

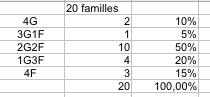
c. Remplir alors le tableau suivant :

PromenadeSurTriangle1

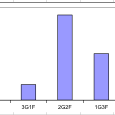
d. Dresser l’histogramme des fréquences.

e. Calculer le nombre moyen de passages par le sommet A pour cette simulation.

Analyse théorique

a. Donner la liste de toutes les promenades possibles de la puce (on peut pour cela utiliser un arbre de choix mais ce n’est pas une obligation). Combien y en a-t-il ?

b. Remplir alors le tableau suivant :

PromenadeSurTriangle2

c. Porter sur l’histogramme dressé à la question précédente les fréquences théoriques que vous venez de calculer.

d. Calculer le nombre moyen théorique de passages par le sommet A.

Vers un grand nombre de promenades

Vers une simulation d’un grand nombre de promenades : utilisation d’un outil informatique

3.1. A l’aide d’une calculatrice ou d’un tableur, on a simulé la promenade de la puce et on a obtenu le tableau suivant :

PromenadeSurTriangle3

a. Remplir la colonne du nombre moyen de passages en A.

b. Représenter sur un graphique ce nombre moyen en fonction du nombre de promenades.

c. Tracer une droite horizontale qui coupe l’axe des ordonnées au nombre moyen théorique de passages en A. Quel commentaire peut-on faire ?

3.2. On effectue maintenant 10 simulations de 100 promenades.

a. On a obtenu le tableau suivant qu’il faut compléter :

PromenadeSurTriangle4

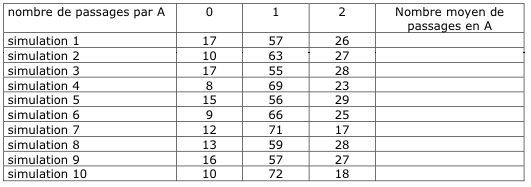
b. En utilisant les 10 simulations précédentes, remplir pour finir le tableau suivant :

PromenadeSurTriangle5

c. Calculer le nombre moyen de passages par le sommet A. Comparer avec le nombre moyen théorique. Quelle conclusion pouvez-vous tirer de cette expérience ?

ANNEXE : Table binaire de nombres aléatoires

PromenadeSurTriangleTableBinaire

Les programmes TI89 ou TI92

Programme promtria() pour 1 promenade de nt secondes

Promenade de nt secondes

Programme promtria()

() Prgm 
Local a
"A→B→C→A"→sensdrct 
"A→C→B→A"→sensind 
ClrIO 
Disp "* Promenade sur un triangle ABC *" 
Disp "sens direct : "&sensdrct
Disp "sens indirect : "&sensind 
Disp "duree de la promenade " 
Prompt nt 
For i,1,nt 
int(2*rand()+1)-1→a[i]
EndFor 
Disp a 
"A"→chain 
For i,1,nt 
If a[i]=0 Then
 ̈ sens direct 
If mid(chain,i,1)="A" Then 
chain&"B"→chain
ElseIf mid(chain,i,1)="B" Then 
chain&"C"→chain 
ElseIf mid(chain,i,1)="C" Then 
chain&"A"→chain
EndIf
ElseIf a[i]=1 Then 
 ̈ sens indirect 
If mid(chain,i,1)="A" Then 
chain&"C"→chain 
ElseIf mid(chain,i,1)="B" Then 
chain&"A"→chain 
ElseIf mid(chain,i,1)="C" Then 
chain&"B"→chain 
EndIf 
EndIf 
EndFor 
Disp chain 
EndPrgm

np promenades de 4 secondes

Programme promtrin()

() Prgm 
Local a,n0,n1,n2 
"A→B→C→A"→sensdrct 
"A→C→B→A"→sensind 
0→n0:0→n1:0→n2 
ClrIO 
Disp "* Promenade sur un triangle ABC *" 
Disp "sens direct : "&sensdrct 
Disp "sens indirect : "&sensind 
Disp " saisir le nombre de promenades " 
Prompt np 
Disp "duree des promenades " 
4→nt 
Disp "4" 
For j,1,np 
For i,1,nt 
int(2*rand()+1)-1→a[i] 
EndFor 
Disp a "A"→chain 
For i,1,nt 
If a[i]=0 Then 
 ̈ sens direct 
If mid(chain,i,1)="A" Then 
chain&"B"→chain 
ElseIf mid(chain,i,1)="B" Then 
chain&"C"→chain 
ElseIf mid(chain,i,1)="C" Then 
chain&"A"→chain 
EndIf
ElseIf a[i]=1 Then 
 ̈ sens indirect 
If mid(chain,i,1)="A" Then 
chain&"C"→chain 
ElseIf mid(chain,i,1)="B" Then 
chain&"A"→chain 
ElseIf mid(chain,i,1)="C" Then 
chain&"B"→chain 
EndIf 
EndIf 
EndFor 
Disp chain 
0→nombrea 
For i,2,dim(chain) 
If mid(chain,i,1)="A" Then 
nombrea+1→nombrea 
EndIf 
EndFor 
If nombrea=0 Then
n0+1→n0 
ElseIf nombrea=1 Then 
n1+1→n1 
Else 
n2+1→n2 
EndIf 
Disp string(nombrea)&" passages en A " 
 ̈Pause 
EndFor 
Disp "n0 "&string(n0) 
Disp "n1 "&string(n1) 
Disp "n2 "&string(n2) 
Disp "nombre moyen de passages en A :" 
Disp (n1+2.*n2)/np 
EndPrgm

Promenades aléatoires sur un tétraèdre

Voici la description du problème extraite d’une fiche de statistiques du document d’accompagnement de seconde des programmes de juin 2000 (« Onze fiches de statistique ») :

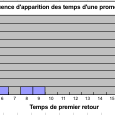
On promène un pion sur les sommets d’un tétraèdre ; toutes les secondes, on déplace le pion d’un sommet à un autre, en choisissant au hasard parmi les trois sommets possibles. On s’intéresse au temps écoulé entre le début de la promenade du pion et le premier retour au point de départ. On limite la promenade à une minute. On utilise des lancers de dés, simulés ou non, pour les déplacements du pion.

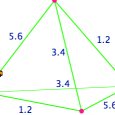
Voici un exemple d’une promenade en 5 coups, avec un codage particulier des arêtes :

Promenade en 5 coups

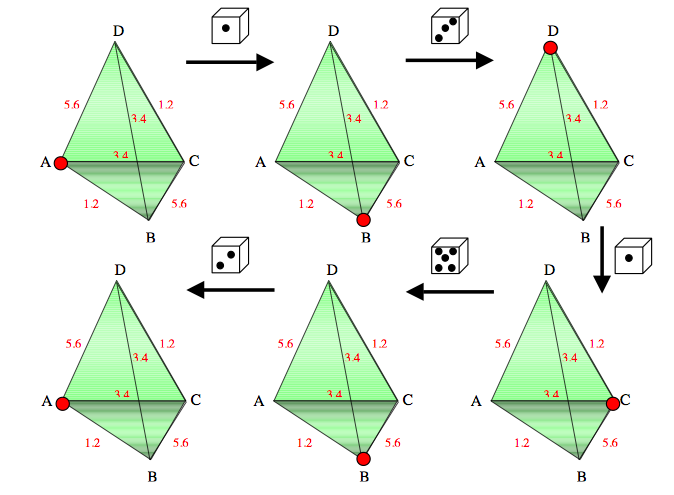
Il s’agit de construire un codage des arêtes du tétraèdre pour une telle promenade.

Codage sur un tableur

PromenadeSurTetraedreEnonce
PromenadeSurTetraedre

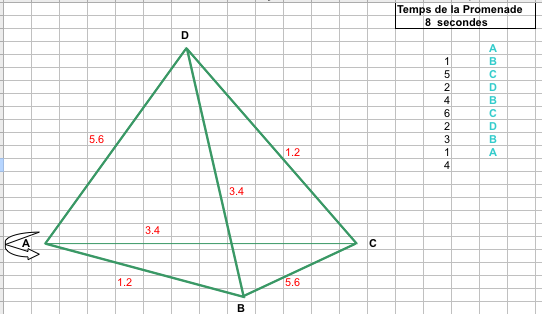
Départ = A en cellule A3

Test 1re position

=SI(OU(C4=1;C4=2);"B";SI(OU(C4=3;C4=4);"C";"D"))

Test 2e position

=SI( OU(ET(A4="B";OU(C5=1;C5=2));ET(A4="C";OU(C5=3;C5=4));ET(A4="D";O U(C5=5;C5=6)));"A"; SI(OU(ET(A4="C";OU(C5=5;C5=6));ET(A4="D";OU(C5=3;C5=4)));"B"; SI(OU(ET(A4="B";OU(C5=5;C5=6));ET(A4="D";OU(C5=1;C5=2)));"C"; SI(OU(ET(A4="C";OU(C5=1;C5=2));ET(A4="B";OU(C5=3;C5=4)));"D"))))

Test 3e position et toutes les suivantes

=SI( OU(A5="A";A5=" ");" "; SI(OU(ET(A5="B";OU(C6=1;C6=2));ET(A5="C";OU(C6=3;C6=4));ET(A5="D"; OU(C6=5;C6=6)));"A"; SI(OU(ET(A5="C";OU(C6=5;C6=6));ET(A5="D";OU(C6=3;C6=4)));"B"; SI(OU(ET(A5="B";OU(C6=5;C6=6));ET(A5="D";OU(C6=1;C6=2)));"C"; SI(OU(ET(A5="C";OU(C6=1;C6=2));ET(A5="B";OU(C6=3;C6=4)));"D")))))

Les codes des macros de la feuille de tableur (codages en Visual Basic)

la macro Promenade aléatoire

Rem Attribute VBA_ModuleType=VBAModule
Option VBASupport 1
Public vitesse As Integer
Public CouleurOff As Integer
Public CouleurOn As Integer


Sub PromenadeAleatoire()
'
' PromenadeAleatoire Macro
' Macro enregistrée le 12/11/2000 par nathalie
'
' Touche de raccourci du clavier: Shift+Ctrl+e
'

Dim TempsPromenade As Integer
Dim numeroAlea As Long
Dim celluleAlea As String
Dim numeroSommet As Long
Dim celluleSommet As String
Dim NomSommet As String
Dim Alea(60) As Integer
Dim nbAlea As Integer



Randomize
'initialisations
For j = 1 To 60
Alea(j) = 0
Next j

'Remplissage du tableau
For j = 1 To 60
Alea(j) = Int(6 * Rnd + 1)
Next j


    Worksheets("PromenadeGraphique").Activate
    Range("P2:R61").Select
    Selection.ClearContents 'efface la sélection
    
    'ecrireSommets (" ")
    'Range("A1:O25").Select
    'Selection.Interior.ColorIndex = CouleurOff

    'initialisations
    vitesse = 1
    CouleurOff = 0
    CouleurOn = 46
    reglage (vitesse)

    'départ de la promenade : écrire A dans la cellule P4
    Range("R4").Select
    Selection.Offset(0, 0).Value = "A"
    NomSommet = "A"
    placer (NomSommet)
    attente (vitesse) 'boucle d'attente

      
     'premier jet de dé
    TempsPromenade = 1
     Range("P5").Select
    ActiveCell.FormulaR1C1 = Alea(TempsPromenade)
    nbAlea = Selection.Offset(0, 0).Value
    attente (vitesse) 'boucle d'attente

    'test première position
    ' =SI(OU(R5=1;R5=2);"B";SI(OU(R5=3;R5=4);"C";"D"))
    
     Range("R4").Select
    If nbAlea = 1 Or nbAlea = 2 Then
        Selection.Offset(1, 0).Value = "B"
        efface (NomSommet)
        NomSommet = "B"
        placer ("B")

        Else
        If nbAlea = 3 Or nbAlea = 4 Then
            Selection.Offset(1, 0).Value = "C"
            efface (NomSommet)
            NomSommet = "C"
            placer ("C")
            Else
            Selection.Offset(1, 0).Value = "D"
            efface (NomSommet)
            NomSommet = "D"
           placer ("D")
        End If
    End If
     TempsPromenade = 2
     
     attente (vitesse) 'boucle d'attente

    'second jet de dé
     Range("P6").Select
    ActiveCell.FormulaR1C1 = Alea(TempsPromenade)
    nbAlea = Selection.Offset(0, 0).Value
    attente (vitesse) 'boucle d'attente

    'Test 2ème position
    '=SI(OU(ET(P5="B";OU(R6=1;R6=2));ET(P5="C";OU(R6=3;R6=4));ET(P5="D";OU(R6=5;R6=6)));"A";
    'SI(OU(ET(P5="C";OU(R6=5;R6=6));ET(P5="D";OU(R6=3;R6=4)));"B";
    'SI(OU(ET(P5="B";OU(R6=5;R6=6));ET(P5="D";OU(R6=1;R6=2)));"C";
    'SI(OU(ET(P5="C";OU(R6=1;R6=2));ET(P5="B";OU(R6=3;R6=4)));"D"))))

    Range("R5").Select
    lettre = Selection.Offset(0, 0).Value
    If (lettre = "B" And (nbAlea = 1 Or nbAlea = 2)) Or (lettre = "C" And (nbAlea = 3 Or nbAlea = 4)) Or (lettre = "D" And (nbAlea = 5 Or nbAlea = 6)) Then
        Selection.Offset(1, 0).Value = "A"
        efface (NomSommet)
        NomSommet = "A"
        placer ("A")
        Else
        If (lettre = "C" And (nbAlea = 5 Or nbAlea = 6)) Or (lettre = "D" And (nbAlea = 3 Or nbAlea = 4)) Then
            Selection.Offset(1, 0).Value = "B"
            efface (NomSommet)
            NomSommet = "B"
            placer ("B")
            Else
            If (lettre = "B" And (nbAlea = 5 Or nbAlea = 6)) Or (lettre = "D" And (nbAlea = 1 Or nbAlea = 2)) Then
                Selection.Offset(1, 0).Value = "C"
                efface (NomSommet)
                NomSommet = "C"
                placer ("C")
                Else
                    If (lettre = "C" And (nbAlea = 1 Or nbAlea = 2)) Or (lettre = "B" And (nbAlea = 3 Or nbAlea = 4)) Then
                    Selection.Offset(1, 0).Value = "D"
                    efface (NomSommet)
                    NomSommet = "D"
                    placer ("D")
                    End If
            End If
        End If
    End If
     
Range("P7").Select
numeroAlea = 6
celluleSommet = "R6"
numeroSommet = 5

Do
     attente (vitesse) 'boucle d'attente
     TempsPromenade = TempsPromenade + 1
     numeroAlea = numeroAlea + 1
    celluleAlea = numeroAlea
    celluleAlea = "P" & celluleAlea
    'troisième jet de dé et suivants
     Range(celluleAlea).Select
    ActiveCell.FormulaR1C1 = Alea(TempsPromenade)
    nbAlea = Selection.Offset(0, 0).Value
    attente (vitesse) 'boucle d'attente
     efface (NomSommet)

    
    'Test 3ème position et toutes les suivantes
'=SI(OU(P6="A";P6=" ");" ";
'SI(OU(ET(P6="B";OU(R7=1;R7=2));ET(P6="C";OU(R7=3;R7=4));ET(P6="D";OU(R7=5;R7=6)));"A";
'SI(OU(ET(P6="C";OU(R7=5;R7=6));ET(P6="D";OU(R7=3;R7=4)));"B";
'SI(OU(ET(P6="B";OU(R7=5;R7=6));ET(P6="D";OU(R7=1;R7=2)));"C";
'SI(OU(ET(P6="C";OU(R7=1;R7=2));ET(P6="B";OU(R7=3;R7=4)));"D")))))
   
   numeroSommet = numeroSommet + 1
    celluleSommet = numeroSommet
    celluleSommet = "R" & celluleSommet
        Range(celluleSommet).Select
    lettre = Selection.Offset(0, 0).Value
    If lettre = "A" Or lettre = " " Then
        Selection.Offset(1, 0).Value = " "
        Else
        If (lettre = "B" And (nbAlea = 1 Or nbAlea = 2)) Or (lettre = "C" And (nbAlea = 3 Or nbAlea = 4)) Or (lettre = "D" And (nbAlea = 5 Or nbAlea = 6)) Then
            Selection.Offset(1, 0).Value = "A"
            NomSommet = "A"
            placer ("A")
            Else
            If (lettre = "C" And (nbAlea = 5 Or nbAlea = 6)) Or (lettre = "D" And (nbAlea = 3 Or nbAlea = 4)) Then
                Selection.Offset(1, 0).Value = "B"
              NomSommet = "B"
              placer ("B")
                Else
                    If (lettre = "B" And (nbAlea = 5 Or nbAlea = 6)) Or (lettre = "D" And (nbAlea = 1 Or nbAlea = 2)) Then
                    Selection.Offset(1, 0).Value = "C"
                    NomSommet = "C"
                    placer ("C")
                    Else
                        If (lettre = "C" And (nbAlea = 1 Or nbAlea = 2)) Or (lettre = "B" And (nbAlea = 3 Or nbAlea = 4)) Then
                        Selection.Offset(1, 0).Value = "D"
                        NomSommet = "D"
                        placer ("D")
                        End If
                    End If
            End If
        End If
    End If
Loop Until (lettre = "A" Or TempsPromenade = 60)  
    'Range("A1:O25").Select
    'Selection.Interior.ColorIndex = CouleurOff
    'Range("B19").Select
    'Selection.Interior.ColorIndex = CouleurOn

    If TempsPromenade < 60 Then TempsPromenade = TempsPromenade - 1
    Range("P2").Select
    Selection.Offset(-1, -1).Value = "Temps de la Promenade"
    Selection.Offset(0, 0).Value = TempsPromenade & "  secondes"
End Sub

Sub placer(sommet As String)
If sommet = "A" Then
                Range("B19").Select
                Selection.Interior.ColorIndex = CouleurOn
ElseIf sommet = "B" Then
                Range("I23").Select
                Selection.Interior.ColorIndex = CouleurOn
ElseIf sommet = "C" Then
                Range("M19").Select
                Selection.Interior.ColorIndex = CouleurOn
ElseIf sommet = "D" Then
                Range("G4").Select
                Selection.Interior.ColorIndex = CouleurOn

End If
End Sub

Sub efface(sommet As String)
If sommet = "A" Then
                Range("B19").Select
                Selection.Interior.ColorIndex = CouleurOff
ElseIf sommet = "B" Then
                Range("I23").Select
                Selection.Interior.ColorIndex = CouleurOff
ElseIf sommet = "C" Then
                Range("M19").Select
                Selection.Interior.ColorIndex = CouleurOff
ElseIf sommet = "D" Then
                Range("G4").Select
                Selection.Interior.ColorIndex = CouleurOff

End If
End Sub

Sub ecrireSommets(s As String)
	Dim faceDé As String
	
       Range("A19").Select
       Selection.Value = "A"
                       
       Range("I24").Select
       Selection.Value = "B"
                
       Range("N19").Select
       Selection.Value = "C"
                
       Range("G3").Select
       Selection.Value = "D"

	'écriture des codes de dés
       Range("D11").Select
       faceDé = "5.6"
       Selection.Value = faceDé
       Range("K22").Select
       Selection.Value = "5.6"
       Range("E22").Select
       Selection.Value = "1.2"
       Range("K12").Select
       Selection.Value = "1.2"
       Range("F18").Select
       Selection.Value = "3.4"
       Range("I15").Select
       Selection.Value = "3.4"
End Sub

Sub attente(v As Integer)
 For k = 1 To Int(100000000 * (1 / (v + 1)))
 Next k
End Sub

Sub reglage(v As Integer)
vitesse = InputBox("Vitesse d'exécution : Entrer un entier compris entre 1 et 1000")
End Sub

la macro Temps de premier retour

Rem Attribute VBA_ModuleType=VBAModule
Option VBASupport 1

Sub TempsDePremierRetour()
'
' TempsDePremierRetour Macro
' Macro enregistrée le 12/11/2000 par nathalie
'
' Touche de raccourci du clavier: Shift+Ctrl+d
'
   
Dim TabPromenade(20, 30) As Integer
Dim NbPromenadesParJeu As Integer
Dim NbJeux As Integer
Dim Jx As Integer
Dim Jp As Integer
 
 
    'initialisation des acquisitions
    NbPromenadesParJeu = 20
    NbJeux = 30
    
    Worksheets("Promenade").Activate
    
    MsgBox "Patientez SVP, le tableur fait ses tirages aléatoires, cela peut prendre plusieurs minutes."
    
    'acquisition des données aléatoires dans le tableau TabPromenade
    For Jx = 1 To NbJeux
        For Jp = 1 To NbPromenadesParJeu
        Range("C4").Select
        ActiveCell.FormulaR1C1 = "=ROUND(RAND()*5+1,0)"
        Range("E6").Select
        TabPromenade(Jp, Jx) = ActiveCell.Value
        Next Jp
    Next Jx
    
    'Sheets("Calculs").Select
    Worksheets("Calculs").Activate
    Jx = 1
    For Each cell_in_loop In Range("B3:B32")
        For Jp = 0 To NbPromenadesParJeu - 1
        cell_in_loop.Offset(0, Jp).Value = TabPromenade(Jp + 1, Jx)
        Next Jp
        Jx = Jx + 1 'changement de jeu
    Next
    
    MsgBox "Fin du calcul. Vous pouvez consulter les histogrammes sur cette feuille."

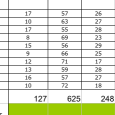
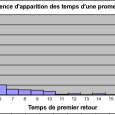
End Sub

Les résultats :

PromenadeSurTetraedre2
PromenadeSurTetraedre3

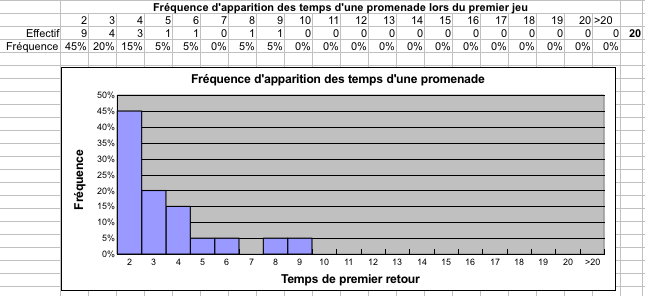
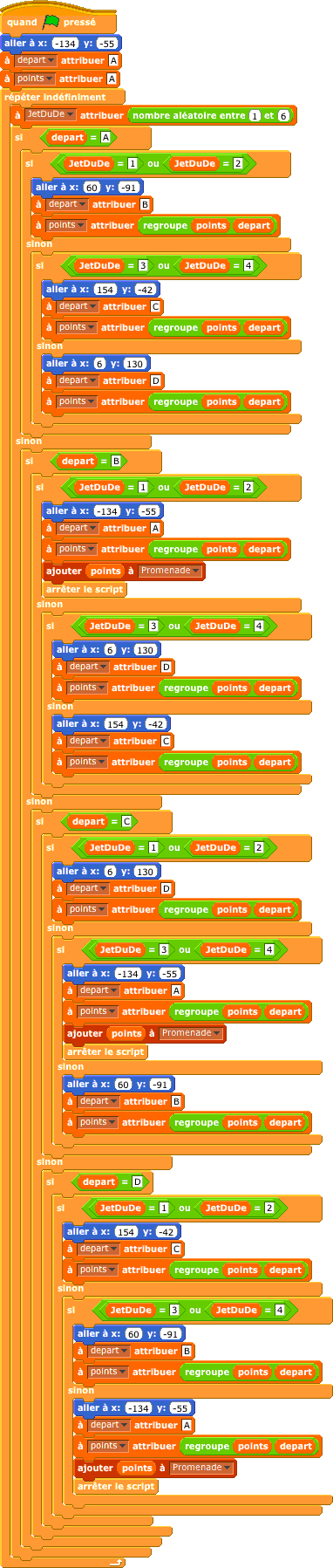
Codage sur Scratch

PromenadeAleatoireTetraedre
Tetraedre2

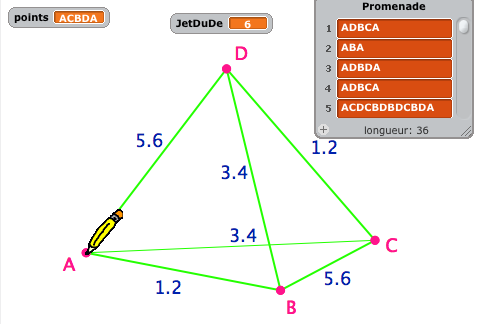
Voir en ligne l’exécution de ce programme ici :
http://scratch.mit.edu/projects/nathalierun/734317

Le petit mot de la fin

Le programme officiel dit explicitement qu’il ne s’agit pas au lycée de faire des programmeurs en classe de mathématiques mais, dans le cadre des simulations en l’occurrence, il est très utile pour les élèves de pouvoir les rendre concrètes et de les réaliser par eux-mêmes (au moins des simples : les simulations de naissances par exemple).


Documents joints

Promenade aléatoire sur un triangle
Promenade aléatoire sur une droite
Simulations de naissances
Simulation 100 familles
Feuille de calcul .ods
Promenade sur un tétraèdre
Feuille de calcul Excel
Promenade sur un tétraèdre
PDF - 128.8 kio

Commentaires

Logo de Nathalie CARRIÉ
mercredi 17 février 2010 à 15h12 - par  Nathalie CARRIÉ

Je viens de mettre en ligne la feuille corrigée. Il y avait un problème dans une ligne du Visual Basic de Excel qui appelait la fonction Application.InputBox alors que dans le Visual Basic de Open Office, elle s’appelle InputBox tout simplement. Ouf ! ;-)

Maintenant, les macros marchent effectivement et s’activent avec la combinaison de touches shift+pomme+e sur Mac. Sur les autres plateformes, pour créer ou modifier l’assignation des macros de la feuille, aller dans Outils -> Personnaliser -> clavier. On choisit alors dans le panneau du haut le raccourci clavier (ctrl+maj+d par exemple), et dans le panneau Catégorie en bas à gauche la macro PromenadeAleatoireTetraedre -> Standard -> module 2 -> fonction « TempsDePremierRetour ».
Faire de même pour assigner la combinaison de touches ctrl+maj+e à la macro PromenadeAleatoireTetraedre -> Standard -> module 6 -> fonction « PromenadeAleatoire ».

Ou, pour lancer la macro PromenadeAleatoire de la feuille PromenadeGraphique, il suffit d’aller dans Outils -> Macros -> Exécuter la macro ->
Panneau Bibliothèque : PromenadeAleatoireTetraedre -> Standard -> Module 6 -> PromenadeAleatoire -> Exécuter.
Pour lancer la macro TempsDePremierRetour de la feuille Calculs, il suffit d’aller dans Outils -> Macros -> Exécuter la macro
Bibliothèque : PromenadeAleatoireTetraedre -> Standard -> Module 2 -> TempsDePremierRetour -> Exécuter.

Bonnes visualisations.

Logo de Alain BUSSER
mardi 16 février 2010 à 22h08 - par  Alain BUSSER

Sous Ubuntu le raccourci Shift+Control+e ne produit rien. Pour lancer la macro il faut aller dans le menu des macros « Open Office Basic » puis cliquer sur « Run macro ».

Pourquoi pas écrire la macro dans un des deux autres langages d’Open Office, Python ou JavaScript, qui possèdent un « switch..case » avec lequel le code est plus léger (enfin je suppose, je n’ai jamais fait de JavaScript sous Open Office) ?

Logo de Nathalie CARRIÉ
mardi 16 février 2010 à 19h59 - par  Nathalie CARRIÉ

Je viens de mettre à disposition les feuilles de tableur correspondant à la promenade sur le tétraèdre, une initialement écrite pour le tableur Excel en Visual Basic, la seconde exportée pour Open Office. Malheureusement, le recalcul de la promenade aléatoire sur le tétraèdre sur la feuille Open Office ne marche pas. Si quelqu’un me trouvait le problème, ce serait magnifique.

Logo de Yves MARTIN
samedi 13 février 2010 à 15h31 - par  Yves MARTIN

Outre les arguments de Alain pour le tableur (par rapport à de la programmation), didactiquement, c’est un changement de cadre particulièrement intéressant à faire fonctionner dans de nombreuses situations, et en particulier ici avec ce mélange sur une même feuille des données, numériques ou non (G, F ...), et des graphiques.
Le fait que l’itération soit éventuellement cachée, par exemple par la poignée de recopie ou les outils logiciels, non seulement n’est pas un obstacle, vu les difficultés rappelées par Alain, mais peut participer à construire des premières images mentales de la séquentialité pour peu qu’on oriente les activités et les observations de nos pratiques en ce sens.

Au passage - mais on commence à être habitué - encore un très bel article. Et comme Nathalie est abonnée aux citations dans le café péda ... le serveur de l’IREM va encore chauffer dans les semaines à venir ;-)

Logo de Alain BUSSER
jeudi 11 février 2010 à 14h11 - par  Alain BUSSER

Très tentant : On a envie de s’y mettre tout de suite ! Cependant, comme on peut le voir dans cet article, l’usage du tableur enlève de la transparence à l’itération, et s’il rend plus aisées les manipulations itératives, c’est au prix d’un certain manque de compréhension sur ce qui se passe « dans la machine ». Le programme de transition de Seconde semble favoriser le « tout algorithmique », ainsi que certains sujets de l’Épreuve Pratique du bac S. Par exemple, pour obtenir au tableur la liste des 20 premiers entiers, il suffit d’entrer 0 et 1 puis d’utiliser la souris pour compléter la liste. Avec un langage de programmation, il faut rédiger la boucle avec un « for..to » ce qui force l’élève à réfléchir à ce qui se passe de façon dynamique dans la boucle (les valeurs successives que prennent l’indice). Ce qui est nettement moins simple...

Citons le document d’accompagnement consacré à l’algorithmique :


– statistique : questions de tris, détermination de certains indicateurs (médiane, quartiles) ;
– probabilités : la modélisation de certains phénomènes à partir de fréquences observées : méthode dite de Monte-Carlo, etc. ;

Or la simulation du NB.SI dans un langage de programmation se fait par quelque chose comme

C’est loin d’être simple ! Créer ce genre de boucle est vécu par les élèves de Seconde comme un problème passionnant, mais difficile... Pour la simulation du $\Sigma$ c’est analogue, donc tout aussi difficile (et passionnant !). Un exemple « simple » est visible dans cet article. Quant à l’étude d’algorithmes de tri pour montrer comment on calcule des quartiles, disons que ni moi ni mes élèves ne sommes prêts pour cela...

En résumé, des tâches aussi simples que le calcul d’une moyenne ou le dénombrement d’objets à l’aide d’une boucle et d’un test, sont assez complexes algorithmiquement parlant en Seconde pour qu’on soit tenté de leur préférer les versions « toutes faites » données par le tableur.

Par contre, la batterie de tests imbriqués qu’on voit ci-dessus (promenade sur tétraèdre, version tableur) est au contraire assez longue pour qu’on puisse lui préférer le switch..case des langages de programmation...