Apprendre à lire des énoncés de problèmes, c’est faire un pas de plus dans la maîtrise de la langue.

Dans la vie courante, les individus ont affaire à des problèmes « pour de vrai ». Or, les situations-pro­blèmes, pure éma­nation scolaire, demandent une représentation mentale de la situation mathématique extrêmement précise.
Avant de rechercher la façon de procéder pour résoudre le problème, il convient de veiller :
à ce que les informations pertinentes, et seulement celles-ci, soient utilisées,
à ce que leur mise en représentation soit cohérente,
pour permettre la réalisation des calculs ou la mobilisation des procédures exigées par la résolution.

Nombre d’erreurs de résolution sont cependant liées à des représentations sémantiques erronées, souvent induites par la polysémie de termes dont les élèves ne retiennent pas le sens en mathématiques. Le « sommet » d’un triangle en géométrie n’est pas nécessairement « en haut », or « sommet » évoque « le haut ».
Un même signifiant, par exemple le verbe « doubler », peut désigner des signifiés différents selon qu’il est associé au mot nombre ou au mot voiture. Un élève peut donner la réponse 6, quand on lui demande de doubler le nombre 5. L’élève associe le verbe « doubler » au mot voiture et dans ce cas, doubler une voiture signifie passer devant.
Il faut du temps avant que les élèves puissent évoquer tout de suite le bon signifié.
Ainsi, à la lecture d’un énoncé de problème, poser aux élèves la question : « Quels mots ne comprenez-vous pas ? », ne permet pas de détecter les difficultés rencontrées avec les mots polysémiques, et les détourne de ce qu’ils ont ici à apprendre : développer des stratégies de compréhension. [1]

Télécharger le diaporama.

Comment lever les difficultés de vocabulaire ?

Tout d’abord, on conviendra d’appeler lexique l’ensemble des mots qu’une langue met à disposition des locuteurs, et vocabulaire l’ensemble des mots utilisés par un locuteur donné dans des circonstances données. Le lexique est une réalité de langue à laquelle on ne peut accéder que par la connaissance des vocabulaires particuliers . [2]
Le vocabulaire regroupe, pour sa part, des sous-ensembles significatifs relevant d’un individu (un auteur, un élève), d’un domaine notionnel, technique ou culturel (vocabulaire du raisonnement, de l’argumentation, de la publicité, etc.), d’une période (vocabulaire du XVIIè), d’une subdivision établie à partir d’autres critères (vocabulaire abstrait, vocabulaire concret, etc.).
Enfin, certains mots appelés mots actifs sont assez bien connus, compris et utilisés d’un individu pour s’exprimer. D’autres, appelés mots passifs, ne sont pas utilisés par lui mais ni toujours compris de façon plus ou moins précise et spécifique.
Enfin, certains mots appelés mots actifs sont assez bien connus, compris et utilisés d’un individu pour s’exprimer. D’autres, appelés mots passifs, ne sont pas utilisés par lui mais ni toujours compris de façon plus ou moins précise et spécifique. Il existe une réelle disparité sur le nombre de rencontres nécessaires pour qu’un mot soit utilisable - donc actif : 4 en moyenne, plus de 10 pour d’autres . [3]

Quel principe didactique ?

L’apprentissage du vocabulaire doit être aménagé, pour trouver son efficacité, selon l’idée que les connaissances stockées en mémoire s’organisent de façon hiérarchique et que les concepts s’emboîtent dans des catégories plus générales comme dans une arborescence . [4]
D’une manière générale, la procédure la plus payante est de faire :

• manipuler, expérimenter le sens des mots dans des contextes appropriés ;
• créer des phrases contextuelles ;
• discuter sur les contextes et sur le sens des mots. [5]

Un outil pour structurer l’apprentissage du vocabulaire
Nous avons dès lors penser une interdisciplinarité d’un des outils d’apprentissage explicite sur les mots aux Mathématiques, à savoir : la corole lexicale car elle permet, entre autres, une relation de sens et une hiérarchie des informations.

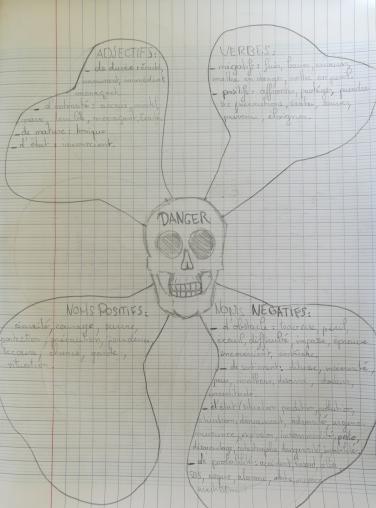
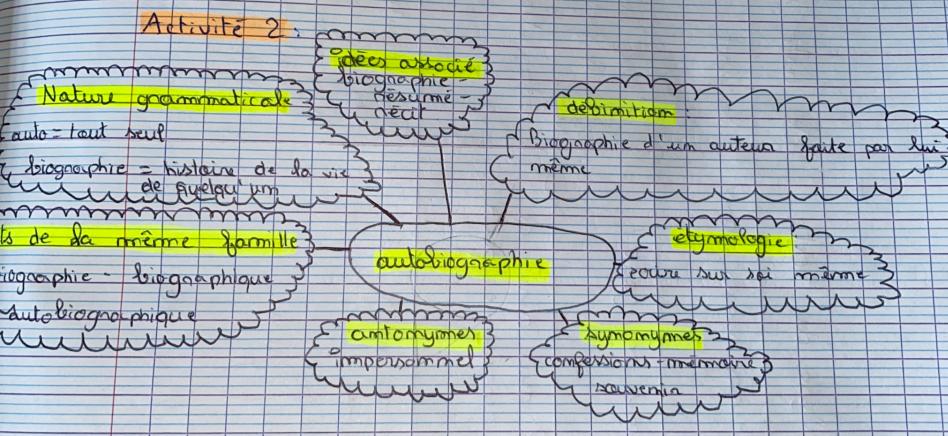
Au centre, le mot, avec toutes ses dimensions potentielles ; sa forme (signifié oral et graphique), son sens (signifié dénoté, mais aussi connoté), son histoire, son statut social… Les divers pétales invitent à des explorations de nature et d’ampleur variées. C’est ainsi que l’on retrouvera des rubriques relevant de branches classiques de la lexicographie (étymologie, champ lexical et analogique, champ sémantique…), d’autres relevant de la sémiologie et de la mythologie, d’autres proches de la syntaxe (traits syntaxiques et lexicaux…), d’autres ouverts sur les multiples dimensions de la culture. Enfin, la dimension individuelle prend toute sa place avec la recherche de mots connotés.

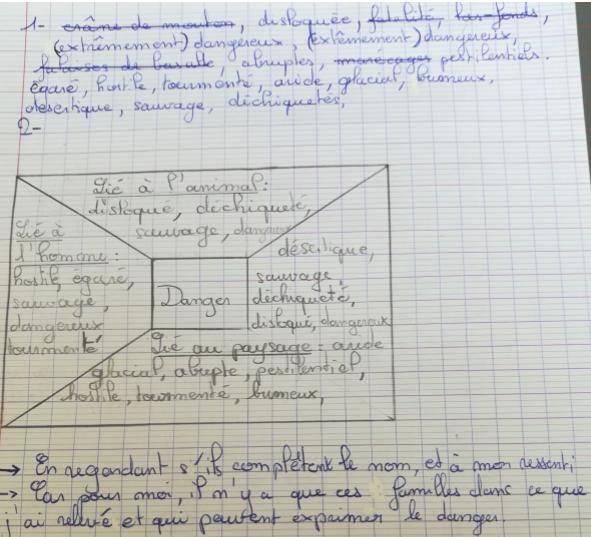
Ici, l’on n’enrichit le vocabulaire des élèves en augmentant leur stock de termes à partir d’une réorganisation du stock de vocabulaire qui était antérieurement disponible, déjà actif.
Cette figuration donne une récapitulation ordonnée des mots réunis et structurés suivant une logique linguistique. Elle offre une image structurée de ce qu’est la langue : des mots reliés entre eux par et dans toutes sortes de réseaux.
L’outil se transforme en « banque de mots » susceptible de nourrir une production écrite, un puissant activateur de la mémoire.

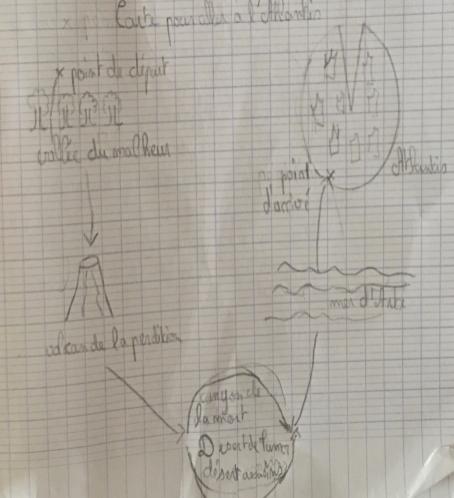
Son transfert aux Mathématiques

Cet enseignement d’enrichissement et de structuration du vocabulaire devient un outil de raisonnement pour entrer dans les énoncés des problèmes. L’objectif, comprendre le choix de l’opération – véritable enjeu de la résolution – lié à l’identification des relations entre les données dont les relations ne sont pas explicitées par le texte.

Son déroulé : l’activité est décomposée… .

1. Sélectionner des informations : catégoriser les mots en explicitant un trait saillant, un point commun
2. Mettre en relation : travailler en réseau autour de la polysémie d’un mot…
3. Appliquer une procédure : Associer un verbe à un choix opératoire dans des contextes variés
4. Déduire
5. Évaluer la capacité à employer à bon escient l’emploi du verbe et le mode opératoire dans un contexte nouveau

Les élèves vont naturellement chercher à séparer les mots qui naturellement seront associées à l’addition (gagner, ajouter...) de ceux qui sont naturellement associés à la soustraction (perdre, enlever...). Tout l’enjeu des séances suivantes est alors de faire prendre conscience que ce n’est pas le verbe qui détermine l’opération, mais bien l’histoire de la situation étudiée.

Pour aller plus loin on peut lire les travaux de Emmanuel Sander sur le recodage sémantique. La corolle lexicale et l’activité d’invention/d’écriture de problème étant ici un moyen pour mettre en oeuvre ce recodage sémantique.

Exploitation et analyse des travaux d’élèves :

Nous utilisons une schématisation inspirée de la classification de Vergnaud sur les problèmes additifs (la même chose peut être faite sur les problèmes multiplicatifs et sur tous les autres types de problèmes) pour « forcer » une situation.
Lorsque je dois inventer un problème dont la réponse peut être obtenue par l’opération est 15-8, il est naturel de partir sur une situation classique : j’ai 15 billes et j’en perds 8.
En forçant l’utilisation du verbe gagner, alors le rôle du 15 change est devient la situation finale : en fin de journée j’ai 15 billes et j’en ai gagné 8 à la récré.

Un point de vigilance doit être sur le verbe avoir : il y a trop de sens autour du verbe avoir. Par exemple : j’ai 15 billes à mon anniversaire signifie-t-il j’ai gagné 15 billes ? au début de mon anniversaire j’avais 15 billes ? à la fin de mon anniversaire j’ai au total 15 billes ?

Conclusion

En conclusion,
Une absence de réponse ou une réponse erronée peuvent signifier une incompréhension de l’énoncé et découler sur une incapacité à mener à bien l’opération demandée.
Apprendre à lire des énoncés de problèmes, c’est donc apprendre à décoder ce système complexe du vocabulaire mathématique, à prendre des repères dans la situation problème, à s’interroger sur les savoirs et savoir-faire à mobiliser et sur l’opération qu’il convient d’effectuer pour réaliser ce qui est demandé.
Des outils, telle la corole lexicale, amènent les élèves à construire une attitude active par rapport à la compréhension.