Bien entendu, les relations de dualité entre droites et points ne sont pas nouvelles, elles sont au cœur même de la géométrie projective (que Pappus soit un théorème ou un axiome de construction du plan projectif) et sont également très présentes en algèbre linéaire. Mais la géométrie projective n’est plus enseignée depuis bien longtemps, tandis que la dualité des espaces vectoriels est elle-même en passe de disparaître des enseignements de base de la licence (elle a déjà disparu des programmes de CGPE).
À la place on fait beaucoup d’autres choses, plus contemporaines, en particulier de la programmation et du calcul formel : c’est par ce dernier que nous allons retrouver, avec un point de vue peut être plus algébrique que d’ordinaire, ces profondes relations entre alignement et concours.
Cet article est structuré en six parties :
1. Écriture algébrique d’alignement de points et concours de droites
2. Version algébrique du théorème de Pappus
3. Approche algébrique de Desargues
4. Coordonnées barycentriques des coniques. Exemples
5. De Pappus à Pascal
6. Autre caractérisation de l’alignement
Dans tout cet article on se place dans un plan affine, a priori sur le corps des nombres réels (plus généralement sur un corps commutatif de caractéristique différente de 2, ce qui semble suffire).
Le déterminant de trois termes a, b, c est noté par le produit mixte [a, b, c] .
1. Coordonnées barycentriques pour points, droites, intersection de droites
1.1. Alignement de 3 points
On se place dans un repère affine $(O, I, J)$ (quelconque) du plan. Étant donnés trois points $M, N, P$ avec leurs coordonnées barycentriques dans $(O, I, J)$, on sait que ces trois points $M, N, P$ sont alignés si et seulement si le produit mixte de leurs coordonnées barycentriques, noté $[M, N, P]$ est nul :
Théorème : $(M, N, P)$ alignés $\Leftrightarrow [M, N, P] = 0$.
C’est simplement un passage des coordonnées cartésiennes aux coordonnées barycentriques. Soit $(A, B, C)$ le repère affine du plan associé au repère cartésien $(A, \overrightarrow{AB}, \overrightarrow{AC})$. L’écriture cartésienne $\overrightarrow{AM}=x \overrightarrow{AB}+y \overrightarrow{AC}$ s’écrit, de manière barycentrique, sous la forme $M=(1-x-y)A+xB+yC$ (avec la notation de Grassmann).
On considère alors trois points $M_1, M_2, M_3$ de coordonnées barycentriques normalisées respectives $M_i \left( \begin{array}{( c )} \alpha_i \\ \beta_i \\ \gamma_i \\ \end{array} \right)$ avec $\gamma_i=1-\alpha_i-\beta_i$ et de coordonnées cartésiennes $M_i (x_i, y_i)$. Avec ces notations, $[M_1,M_2,M_3] = \begin{array}{| l c r |} \alpha_1 & \alpha_2 & \alpha_3 \\ \beta_1 & \beta_2 & \beta_3 \\ \gamma_1 & \gamma_2 & \gamma_3 \\ \end{array}$.
Les trois points $M_1, M_2, M_3$ sont alignés ssi les deux vecteurs $\overrightarrow{M_1M_2}$ et $\overrightarrow{M_1M_3}$ sont liés, soit ssi $\begin{array}{| c c |} x_2-x_1 & x_3-x_1 \\ y_2-y_1 & y_3-y_1 \\ \end{array} = 0.$
Ceci est équivalent à $\begin{array}{| cc c |}
1 & 0 & 0\\
x_1 & x_2-x_1 & x_3-x_1 \\
y_1 & y_2-y_1 & y_3-y_1 \\
\end{array} = 0$, ou encore, en ajoutant la première colonne aux deux autres, à $\begin{array}{| cc c |}
1 & 1 & 1\\
x_1 & x_2 & x_3 \\
y_1 & y_2& y_3 \\
\end{array} = 0.$
En retranchant les deux dernières lignes de la première, c’est aussi équivalent à :
$\begin{array}{| cc c |}
1-x_1-y_1 & 1-x_2-y_2 & 1-x_3-y_3\\
x_1 & x_2 & x_3 \\
y_1 & y_2& y_3 \\
\end{array} = 0$, ce qui n’est autre que le déterminant initial nul : $\begin{array}{| l c r |}
\alpha_1 & \alpha_2 & \alpha_3 \\
\beta_1 & \beta_2 & \beta_3 \\
\gamma_1 & \gamma_2 & \gamma_3 \\
\end{array}=0 $, c’est-à-dire $[M_1,M_2,M_3]=0.$
Cette preuve a été faite pour des cordonnées normalisées. Compte tenu des propriétés trilinéaires des déterminants, il est clair que c’est aussi une équivalence pour des coordonnées barycentriques non normalisées.
(fin du bloc de la preuve du résultat)
Or le produit mixte $[u, v, w]$ — qui n’est autre que le déterminant $det(u, v, w)$ — est justement mixte au sens où il s’écrit avec le produit vectoriel et le produit scalaire : $[u, v, w] = (u \wedge v).w$. C’est même, en général, la définition du produit vectoriel, qui, comme application, est bilinéaire et antisymétrique.
1.2. Coordonnées barycentriques de droites. Équations tangentielles
Ainsi, $M$ appartient à la droite $(AB)$ s’écrit aussi $[A, B, M] = 0$, ou encore $(A \wedge B).M = 0$.
On appelle coordonnées barycentriques de la droite $(AB)$, les coordonnées de $A \wedge B$. Si $M$ a pour coordonnées barycentriques $(x, y, z)$ et $A \wedge B$ s’écrit $(a, b, c)$, la nullité du produit scalaire précédent devient $ax+by+cz=0$. Cette équation s’appelle une équation tangentielle de la droite $(AB)$. C’est une relation qui caractérise les coordonnées barycentriques d’un point $M$ de cette droite $(AB)$.
Théorème : $M \in (AB) \Leftrightarrow (A \wedge B).M = 0$.
Remarques :
• Ces rappels ne sont pas un cours, ce ne sont que des rappels. Il conviendrait par exemple de montrer le sens réciproque : l’ensemble des points $M(x,y,z)$, tel que $ax+by+cz=0$, avec $a, b, c$ non tous égaux — sinon les points A et B seraient confondus — est bien une droite affine.
• De même il faudrait préciser à chaque fois que le triplet de coordonnées (x, y, z) est non nul.
• Tout ceci est très bien traité dans de nombreux cours, en ligne ou dans des ouvrages classiques comme les deux cités en référence en fin d’article.
• Ces ouvrages en général n’utilisent pas la notation du produit vectoriel, plus anglo-saxonne semble-t-il, mais on la trouve aussi chez Daniel Perrin dans son dernier livre de géométrie, disponible en ligne.
1.3.Exemples et explorations dynamiques
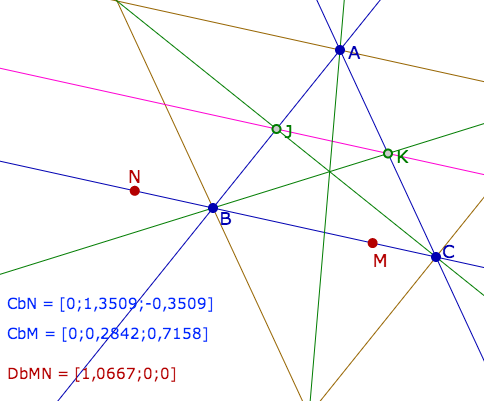
Dans la figure dynamique suivante vous êtes invité à placer les points M et N sur les différentes droites : côtés du triangles ABC, droites parallèles à ces côtés passant par le sommet opposé, les médianes, ou la droite des milieux (JK). Pour cela les deux points M et N sont aimantés par ces droites, ce qui permet d’avoir des résultats précis sur les différentes coordonnées barycentriques.
Dans chaque cas, observer les coordonnées des points M et N et les coordonnées barycentriques de la droite concernée. Confirmer par du calcul vectoriel avec le théorème ci-dessus (détails et illustrations dans le bloc après la figure).
Commentaires de la figure à l’ouverture
$M$ et $N$ sont sur la droite $(JK)$, on s’intéresse donc à une équation tangentielle "de la droite des milieux".
On lit, dans la liste DbMN — pour Droite barycentrique $(MN)$ — qu’une équation barycentrique de $(MN)$ est ici $x-y-z=0$ car le triplet est de la forme $[a,-a,-a]$.
Les coordonnées barycentriques normalisées de $M$ et $N$ illustrent que la coordonnée sur $A$ est toujours $1/2$. Cela vient du fait que les coordonnées $M(x, y, z)$ doivent vérifier à la fois $x+y+z=1$ (écriture normalisée) et $x-y-z=0$, soit, par somme, $2x=1$ d’où le résultat.
Il en résulte que les points $M$ et $N$, sur $(JK)$, ont leurs coordonnées barycentriques de la forme $[0,5 ; y ; 0,5 - y]$.
Calcul de l’équation barycentrique de (JK)
On part simplement de $J(1, 1, 0)$ et $K(0, 1, 1)$, alors $J \wedge K = (1, -1, -1)$.
Ce qui est bien illustré dans la figure ci-dessus (à l’ouverture, à un coefficient d’homogénéité prés). On voit que l’on n’a pas besoin d’utiliser les écritures barycentriques normalisées.
Le lecteur est invité à prendre le temps d’explorer d’autres situations, par exemple les quatre illustrations du bloc suivant, ou poursuivre avec d’autres droites non traitées.
La droite (BC)
$B \wedge C = A$, et donc la droite $(BC)$ a pour coordonnées barycentriques $(1, 0, 0)$, soit encore pour équation tangentielle $x=0$.
Les points de $(BC)$ ont alors des coordonnées barycentriques normalisées de la forme $(0, y, 1-y)$.



Commentaires