Interlude : Installation d’un réseau wifi local [1]
Mon vénérable internaute, parfois, besoin se fait sentir de partager des documents lors d’une modeste présentation. Ô certes, l’Internet nous à rendu facile l’utilisation de liens vers le web, des fichiers drobpox ou drive de google ou tout autre type de partage de données sur le cloud. Mais nul n’est à l’abri de se sentir vermine si toutefois aucune connexion internet n’est disponible ! A-t-on tous le courage de la goutte d’eau qui ose tomber dans le désert ? Seul l’aventurier intrépide se lançe à corps perdu en hurlant « banzaï ! » dans la configuration d’un routeur wifi et d’un serveur apache.
Toutefois, si comme moi, d’aujourd’hui, du tonnerre viendra la montagne ; il existe une solution assez simple à mettre en œuvre et que votre humble serviteur vous propose de suivre. Pas d’inquiétude, vous ne risquez rien, il y en a pour 5 mn et dites vous bien, Ô respectable internaute, qu’un imbécile qui marche ira toujours plus loin que deux intellectuels qui restent assis...
Entendons nous bien, l’utilisation d’un point d’accès wifi et d’un serveur web reste obligatoire ! Il faudra donc passer par ces deux étapes. Mais au lieu de se servir d’une box wifi, nous allons transformer un ordinateur portable en point d’accès et utiliser un serveur rudimentaire, facile à installer et à lancer, qui nous servira juste à diffuser des pages HTML statiques.
Le point d’accès wifi
C’est au pied du mur qu’on voit le mieux le mur : une petite vidéo que j’ai réalisée pour vous mettre sur les bons rails :
Voici la manip avec Ubuntu [2]. Pour window$ débrouillez vous [3]
Nous allons utiliser le gestionnaire de réseau par défaut d’Ubuntu et un tout petit hack (modification).
1. Cliquez sur l’icône Réseau dans la barre supérieure principale, puis sur « Modifications des connexions... ».
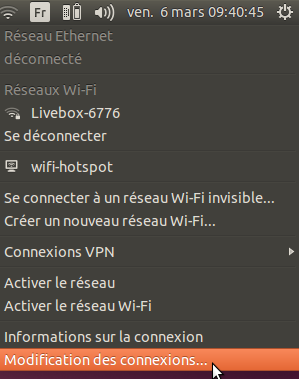
2. Cliquez sur le bouton « Ajouter » dans la fenêtre pop-up qui apparait.
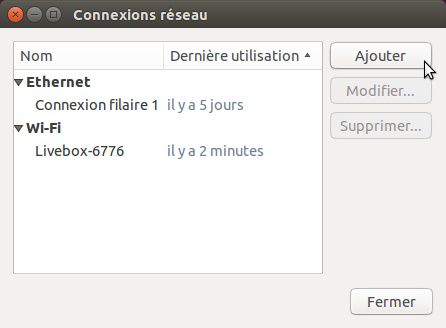
3. Choisissez « Wi-Fi » dans le menu déroulant lorsque vous êtes invité à sélectionner un type de connexion, puis cliqueé sur « Créer ».
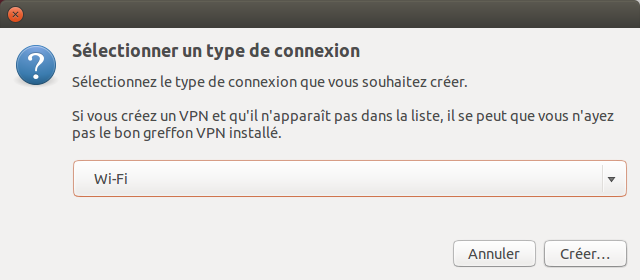
4. Dans la fenêtre suivante :
- Dans le champ « Nom de la connexion » : taper un nom. celui-ci sera utilisé plus tard(par exemple « wifi-hotspot »).
- Puis dans l’onglet Wi-Fi (vous y êtes déjà normalement)
- Dans le champs SSID entrez la même chose que le « Nom de la connexion » que vous avez choisit (pas d’espace, pas d’accents pour eviter les tracas ex :« wifi-hotspot »)
Sélectionnez le mode : Infrastructure - Adresse MAC du périphérique : sélectionnez votre carte sans fil à partir du menu déroulant (propablement étiquetée wlan0).

5. Allez à l’onglet Sécurité Wi-Fi, sélectionnez le type de sécurité WPA et WPA2 Personal et définir un mot de passe (ou pas, vous pouvez choisir aucune sécurité si vous souhaitez que votre hotspot soit ouvert).
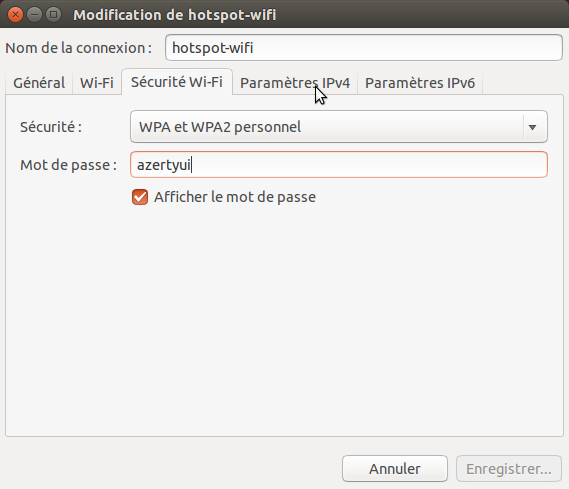
6. Allez à l’onglet Paramètres IPv4, depuis la liste déroulante « Méthode » sélectionner « Partagé avec d’autres ordinateurs ».
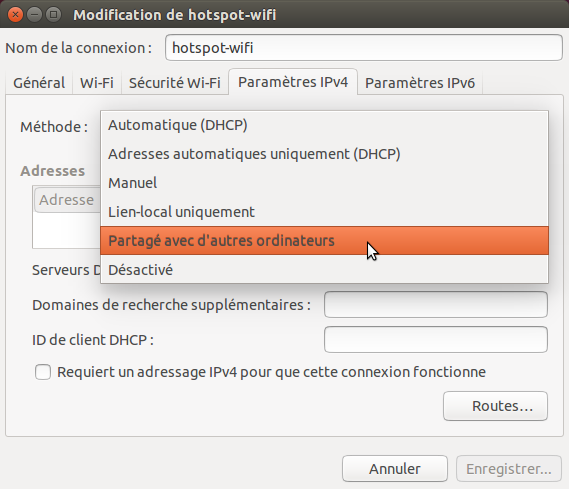
Lorsque vous avez terminé, cliquez sur le bouton Enregistrer.
- Dans le champs SSID entrez la même chose que le « Nom de la connexion » que vous avez choisit (pas d’espace, pas d’accents pour eviter les tracas ex :« wifi-hotspot »)
Après les étapes ci-dessus, un fichier de configuration est créé sous /etc/NetworkManager/system-connections/. Le nom du fichier est le même que le nom de connexion que vous avez tapé à l’étape 4.
Maintenant, appuyez sur Ctrl + Alt + T sur le clavier pour ouvrir un terminal. Quand il s’ouvre, collez les commandes ci-dessous et appuyez sur Entrée pour modifier le fichier de configuration :
-
gksu gedit /etc/NetworkManager/system-connections/hotspot-wifi
Remplacer hotspot-wifi avec le nom que vous avez tapé à l’étape 4, si vous n’avez pas choisit celui-la ! Lorsque le fichier s’ouvre, trouver la ligne
mode = infrastructure
et la changer en
mode = ap
Enfin enregistrer le fichier.

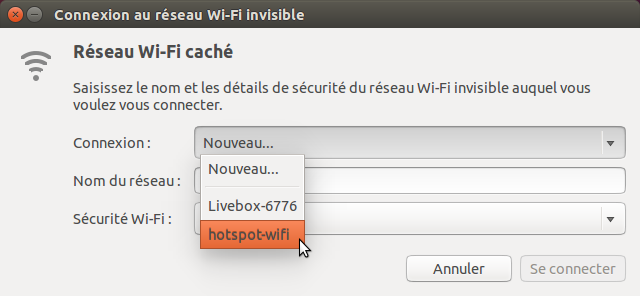
Quand tout est fait, activer le WiFi depuis l’icône de gestionnaire de réseau sur la barre des taches principales dans le coin supérieur droit. Votre ordinateur devrait se connecter automatiquement au hotspot que vous avez créé. Si vous ne le voyez pas, cliquez sur "Se connecter a un réseau Wi-Fi invisible... » dans le même menu et sélectionnez le dans la liste déroulante.
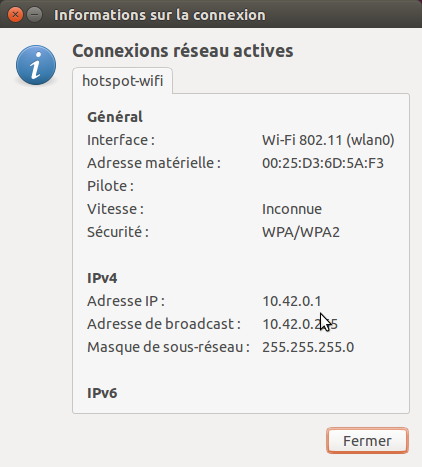
Une dernière chose importante : il faut noter l’adresse ip de votre machine, ce sera celle de votre serveur, elle servira donc plus tard ! Cliquer en haut à gauche sur l’icone de gestionnaire de réseau sur la barre des taches principales dans le coin supérieur droit, puis sur information sur la connexion puis notez l’adresse IPV4 (probablement de la forme http://10.42.0.1).En ligne de commande ce sera avec ifconfig ou ip address

Maintenant, vous pouvez rechercher et vous connecter au point d’accès à partir d’une tablette ou d’un smartphone et profitez-en ! Evidemment, pour que tout le monde puisse bénéficier de l’Internet, il faut connecter votre ordinateur à Internet par le biais d’un câble RJ-45. Cependant, comme mentionné au début de l’article, il est possible qu’auncune connexion à Internet ne soit disponible... Qu’a cela ne tienne, nous allons mettre en place un « web local »...Attachez vos ceintures !
Le serveur web
Pour diffuser de l’information sur un réseau, il faut et il suffit que l’ordinateur ouvre « un numéro de port de données » (en général le 8080) depuis l’un de ses répertoires afin d’autoriser des « clients » (tels les navigateurs) à s’y connecter. Dès lors, en demandant à un navigateur de se rendre à l’adresse IP du serveur suivi du port ouvert en les séparant par deux points (http://10.51.0.1:8080), le navigateur sera en mesure d’afficher le contenu du répertoire partagé par le serveur.
Charabia ? Pas d’inquiétude, tout va s’éclaircir :
Nous allons installer node.js, un environnement en javascript permettant de lancer un programme (npm) qui installera le serveur (http-server).
Installation de NodeJS
[4]
Ouvrez une invite de commande par la combinaison de touches suivante : Ctrl + Alt + T
- Ajoutez le dépot de Chris Lea (Chris Lea maintient un dépot avec des versions stables plus récentes de Nodejs) dans vos sources de logiciels :
sudo apt-add-repository ppa:chris-lea/node.js
- Rechargez la liste des paquets :
sudo apt-get update
- Installez les paquets nodejs.
sudo apt-get install nodejs
Installation de http-server
[5]
- Toujours depuis le terminal, lancer la commande suivante :
npm install http-server -g
- Si jamais vous rencontrez une erreur à l’installation, tant pis [6], faites ceci (installation en mode super user) :
sudo npm install http-server -g
Lancement du serveur
[7]
- Il ne vous reste plus qu’a lancer le serveur depuis le répertoire que vous souhaitez partager. Exemple le dossier « irem » sur mon « Bureau » :
cd ~/Bureau/irem
- Puis lancer le serveur :
http-server -p 8080
Visiter le dossier depuis un navigateur
Ouvrez votre navigateur favori, puis dans la barre d’adresse, tapez l’adresse ip de votre serveur suivi du numéro de port précédemment ouvert :
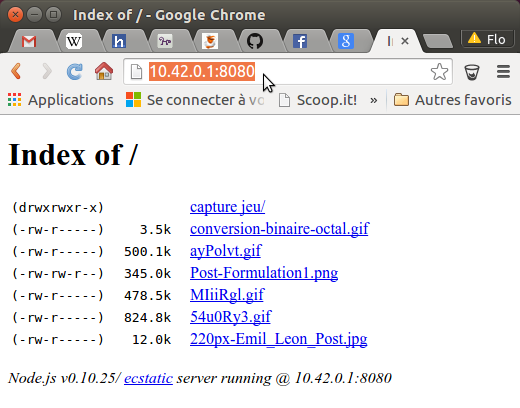
Ok c’est moche, mais c’est partagé ! Pour rendre tout ça très beau, il faudrait y ajouter un soupçon d’HTML5 et deux pincées de CSS3 !
Présenter son dossier partagé : Un site web statique vite fait !
Les navigateurs sont des explorateurs de fichiers d’un genre spécial : ils réagissent de manière particulière à certains type de fichiers : ceux dont l’extension est .html. Faire pointer un navigateur vers un fichier html va le forcer à afficher non pas le code mais son interprétation. Ainsi, utiliser des pages html pour présenter vos liens est une touche de finition qui ne saurait être qu’appréciée. Mais là encore, si l’on veut faire preuve de professionnalisme, les bras peuvent nous en tomber sous le poids du fardeau qui s’annonce. Un site web, c’est beaucoup de balises ; c’est du css, du javascript, des images, une petite icone pour l’onglet du navigateur. Peut-être même faut-il songer à entretenir ce code et donc prévoir une arborescence adaptée pour une évolution et des modifications aisées ? Scinder le code en séparant css, javascript et html ? Qu’en est-il des recommandations du w3c à propos des dernières spécifications du html5 [8]... Toutes ces questions ne sont pas superflues, elles s’imposent aux concepteurs sérieux. N’existe-t-il donc pas un outil qui pourrait nous préparer une trame, prete à remplir, aux normes, compatible avec l’ensemble des navigateurs et ordonnée selon une arborescence claire et intuitive afin de nous faire gagner un temps précieux au démarrage ? HTML5 Boilerplate (H5BP) [9] : C’est exactement cela !
Pour s’en tenir à sa description : HTML5 Boilerplate vous aide à construire des applications ou des sites Web rapides , robustes et adaptables . Démarrer votre projet avec la connaissance et l’effort combiné de centaines de développeurs, le tout en un petit paquet.
En allant sur Github.com vous pouvez récupérer la dernière version dans un fichier zip. Mais faisons encore mieux ! Nous allons passer par le site Initializr qui va configurer pour nous l’archive zip afin qu’elle contienne le strict minimum nécessaire à notre ambition : une toute petite page html !
Rendez vous donc sur http://www.initializr.com/ et cochez les cases suivantes :

- Mobile-first Responsive [10] : Afin d’avoir une page html prête à l’emploi et qui s’adapte aux écran d’ordinateur, de tablette et de smartphone de façon réactive.
- Just HTML5shiv [11] : Nous allons faire simple, HTML5shiv c’est HTML5 (même pour les vieux Explorateur$ Internet) .
- .htaccess [12] : ce petit fichier indiquera au serveur qu’il faut orienter le navigateur vers le fichier index.html lorsque celui-ci cherchera à explorer le dossier partagé
- favicon [13] : c’est une petite image qui s’affiche à coté du titre de la page dans l’onglet du navigateur, c’est la petite cerise sur le gâteau !
Le reste peut-être décoché, ensuite vous pouvez cliquer sur « Download it ! ».

L’archive zip que vous allez télécharger contiendra tout ce dont vous avez besoin pour commencer. Décompressez le tout dans votre fameux dossier partagé et contemplez l’œuvre prête à la finition !

Changer le titre et les liens sera un jeu d’enfant pour celui qui comprend quelques bribes des langages du web [14].
Le jeu électronique : Émilio Posti on the bit
Pour jouer à ce jeu (de ouf !), le plus simple est encore de l’essayer en ligne en vous rendant à cette adresse : http://zotweb.re/irem/game-wang
Si vous préférez télécharger le code source, faites le depuis github pour obtenir la derniere version : https://github.com/rodeofly/game-wang
d’Emil Post à Emilio Posti : un post-it
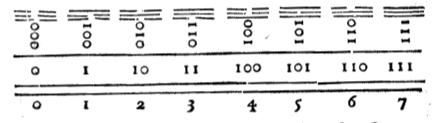
Dans son article original de 1936, Emil Post parle d’un « worker » (traduit par « ouvrier », c’est Emilio ci-dessous) qui coche (« mark ») des boîtes (« spaces or boxes ») dans (ou par-dessus) lesquelles il se déplace au cours de son travail. Mais « box » peut se traduire aussi par « case à cocher » (« checkbox ») et en remplaçant les traits verticaux suggérés par Emil Post, par des coches en deux traits, sa configuration ressemblerait plutôt à ceci :

Ci-dessus l’ouvrier Emilio a coché la boîte numéro 2 et seulement celle-ci. Voici comment Emil Post voyait les boîtes en question [15] :

Bon, et que peut-il faire, cet ouvrier, devant tout cet alignement de cases à cocher (ou pas) ?

Pour les (a) et (b), un seul bouton suffit, qui a pour effet de cocher et décocher alternativement la case sur laquelle se trouve Emilio. Ce bouton est sur la droite de la Wang-boy :

En-dessous de ce bouton, il y a un bouton sans mention mais en-dessous duquel est écrit « right » : Il sert donc à réaliser l’instruction (c).
Sur la gauche de la Wang-boy, il y a un bouton en-dessous duquel est écrit « left ». L’action de ce bouton réalise donc l’instruction (d). Enfin l’instruction (e) est associée à l’autre bouton de gauche, celui qui est marqué « ? » :

Ce bouton affiche la case, cochée ou non, sur laquelle Emilio est debout (les cases sont fixées aux planches formant un pont, qu’Emilio doit consolider en cochant les cases demandées). Emilio ne peut pas complètement traverser le pont, ce qui fait qu’une fois qu’on est tout à gauche, le bouton « left » est inopérant. Par contre, une fois qu’Emilio est à droite du pont, le bouton « right » lui permet de grimper dans le cocotier où se trouve son QG, et là les actions des boutons ne sont plus les mêmes :
- « right » est inopérant ;
- « left » permet de revenir sur le pont ;
- « ? » affiche la totalité des cases du pont (représentation binaire du nombre actuellement représenté) ;
- La case au coche permet de valider le nombre représenté en binaire sur le pont.
Remarque : Les enfants en cours d’apprentissage de la lecture semblent mieux comprendre que les adultes habitués aux modes d’emploi, le fonctionnement du jeu. En particulier, le fait que le bouton pour aller à gauche soit situé à gauche, leur semble naturel. Les explications ci-dessous sont donc a priori réservées aux adultes...
Un exemple de partie détaillée : On doit représenter le nombre 3 (soit 11 en binaire), le point de départ étant l’arbre, et aucune case n’est actuellement cochée (on est dans le jeu A). Il faut donc appuyer une fois sur la touche « left » pour être sur la case « 1 », puis une deuxième fois pour être sur la case « 2 » :

Ensuite, un appui sur la touche de validation permet (avec un son évocateur) de cocher celle-ci :

Au cas où on aurait un doute (par exemple parce qu’on aurait coupé le son), on actionne la touche « ? » et un affichage provisoire confirme que la case est cochée :

Ensuite, on doit aller vers la droite avec le bouton iguane idoine, cocher la case « 1 » avec le bouton idoine, aller dans l’arbre avec le bouton « right » (all right ?), et faire un petit bilan avec « ? » :
Vu qu’on a bon, on peut valider sa réponse, ce qui déclenche une danse de la victoire chez Emilio (si on avait fait faux, Emilio aurait eu un sourire gêné et perdu une vie) :

Enfin, voici une petite démo pour comprendre les règles de ce jeu démoniaque expliquée par un jeune padawan de 6 ans [16] !
algorithmes de conversion
Le jeune Ky-Mani ci-dessus utilise visiblement l’algorithme glouton pour convertir 12 en binaire (et avec une rapidité impressionnante). Celui-ci consiste à
- cocher la plus grande case inférieure ou égale au nombre (restant) à convertir ;
- soustraire la valeur de cette case au nombre à convertir, et retourner à l’étape précédente pour la différence...
Cette méthode ne fait pas l’unanimité en terminale, où certains élèves préfèrent faire l’inverse :
- cocher la case 1 si le nombre à convertir est impair ;
- dans ce cas soustraire 1 pour rendre le nombre pair ;
- aller à gauche ;
- diviser le nombre obtenu par 2, puis retourner à l’étape du départ...
Pour convertir 12 en binaire, l’algorithme donne ceci :
- 12 est pair, on ne coche pas la case 1 ;
- 6 est pair, on ne coche pas la case 2 ;
- 3 est impair, on coche la case 4 et on soustrait 1 ;
- 1 est impair, on coche la case 8 et on soustrait 1 ;
- on a 0, on a fini.
Ce qui donne bien 1100 pour la représentation binaire de 12.
Gottfried Wilhelm Leibniz
Le vénérable Gottfried Wilhelm Leibniz, sinophile s’il en est, est vraiment un précurseur de l’informatique théorique avec son concept de calculus ratiocinator, mais également avec la promotion du calcul en binaire qu’il a faite au sein de l’académie des sciences en 1703. En voici quelques extraits :
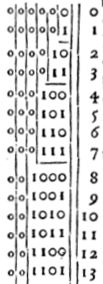
- Tableau des nombres binaires
| La version Leibniz | la version Wang |
|

|
Comment marche le puzzle qui le reconstruit
On commence le puzzle par le coin en haut à droite ; on constate qu’il faut un bord supérieur bleu et un bord droit rouge :

Or parmi les pièces disponibles dans le jeu, il n’y en a qu’une qui convienne, c’est celle du haut :

On place donc celle-ci dans le puzzle. Elle porte le chiffre 1 et donc le premier nombre entier s’écrit 1 en binaire. Du coup la pièce suivante doit avoir un bord supérieur et un bord droit tous les deux bleus. Ces pièces, entièrement bleues, portent le chiffre 0 ce qui fait que le premier entier non nul ne s’écrit pas réellement 1 mais 00001 en binaire. Une fois la première ligne remplie, la seconde ligne commence, à droite, par une pièce ayant un bord supérieur et un bord droit rouges tous deux :

C’est la troisième pièce en partant du haut :

Et ainsi de suite...
Remarques sur ce tableau
Comme les nombres sont alternativement pairs et impairs, la dernière colonne est formée d’une alternance de 0 et de 1. L’avant-dernière colonne, elle, est formée d’une alternance de 00 et de 11. Et ainsi de suite pour les autres colonnes. Leibniz s’en est émerveillé, mais surtout il a constaté des phénomènes similaires dans d’autres tables binaires :

Par exemple, voici la table des carrés en binaire :
000000001
000000100
000001001
000010000
000011001
000100100
000110001
001000000
001010001
001100100
001111001
010010000
010101001
011000100
011100001
100000000
100100001
101000100
101101001
110010000Pour la construire avec affichage des 0 à gauche et alignement, on a utilisé l’algorithme suivant :
-
- boucler sur n
- calculer son carré n²
- ajouter 65536 pour avoir un « 1 » tout devant
- transcrire en binaire avec toString(2) qui renvoie la chaîne de caractères représentant le nombre en binaire
- supprimer le « 1 » initial et quelques « 0 » avec c[8..] qui renvoie les lettres à partir du rang 8 dans le mot formé par l’écriture binaire.
En CoffeeScript, programmé sur alcoffeethmique, le script s’écrit ainsi :
for n in [1..20]
c = n*n
c += 65536
c = c.toString 2
c = c[8..]
affiche cOn constate alors que la première colonne est à nouveau formée d’une alternance de 0 et de 1. Mais la seconde colonne (en partant de la droite) est formée uniquement de « 0 ». Pour avoir la troisième colonne, on extrait les 3 derniers caractères de la représentation binaire, puis le premier caractère de la sous-chaîne obtenue, et en concaténant les chiffres binaires, au fur et à mesure, à une chaîne initialement vide. Ce qui donne un affichage en ligne plutôt qu’en colonne, et le script que voici
motif = ""
for n in [1..20]
c = n*n
c += 65536
c = c.toString 2
c = c[8..]
motif += c[-3..][0]
affiche motifLe motif obtenu est 01000100010001000100 qui est périodique, de période « 0100 ». Les chiffres des huitaines forment la période 00101000, les chiffres des seizaines forment la période 0001101010110000.
La même technique permet d’explorer les cubes :
-
- les chiffres des unités forment la période 10
- les chiffres des deuxaines forment la période 0010
- les chiffres des huitaines forment la période 00001010
- les chiffres des seizaines forment la période 0110110011000110...
Ce dernier cas se voit avec le script suivant :
motif = ""
for n in [1..40]
c = n*n*n
c += 65536
c = c.toString 2
c = c[8..]
motif += c[-4..][0]
affiche motifPour les nombres triangulaires, on peut utiliser ce script :
motif = ""
for n in [1..40]
c = n*(n+1)/2
c += 65536
c = c.toString 2
c = c[8..]
motif += c[-1..][0]
affiche motifOn voit alors que
-
- les chiffres des unités donnent la période 1100
- les chiffres des deuxaines donnent la période 01111000
- les chiffres des quatraines donnent la période 0010111111010000
- les chiffres des huitaines donnent la période 00011010100111111110010101100000
- Algorithme de conversion décimal -> binaire :

Remarque : En 1703 en France, on n’utilisait le système décimal ni pour les poids ni pour les monnaies. Le système monétaire binaire proposé par Leibniz est donc nettement plus simple que le système monétaire de l’Ancien Régime. Quand au système de poids binaires, les « essayeurs » peuvent l’essayer en ligne.
La version d’Alembert
Voici l’article de l’Encyclopédie (mathématiques) de d’Alembert, consacré au calcul binaire (1783) :




Cet algorithme peut aider à gagner à ce jeu, auquel les participants munis d’un appareil connecté à la wifi ont pu jouer avec beaucoup de concentration.
- Opérations en binaire

Addition binaire
Voici la manière d’utiliser le puzzle d’addition binaire pour effectuer 6+10 :
-
- On convertit 6 en binaire : 110
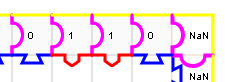
L’un des opérandes est représenté en binaire en haut du puzzle, l’autre, en bas.
-
- On convertit 10 en binaire : 1010 (le jeu de Wang-Post est un bon entraînement !) :

-
- On complète le puzzle pour effectuer l’addition :
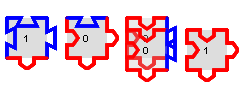
On commence par la droite ; on constate que la première pièce à poser est bleue en haut, en bas et à droite (le fait qu’elle est bleue à droite veut dire qu’il n’y a pas de retenue). Or une seule pièce convient, c’est celle de gauche :

On la pose donc :
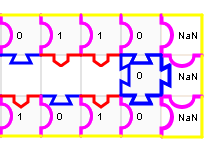
Elle porte le chiffre 0 ce qui veut dire que le chiffre des unités de la somme est 0. Et son bord gauche est bleu ce qui veut dire qu’il n’y a pas de retenue. Du coup il faut maintenant une pièce ayant des bords haut bas rouges, et un bord droit bleu. C’est l’avant-dernière pièce :
Elle porte le chiffre 0 donc le chiffre des deuzaines de la somme est 0 :
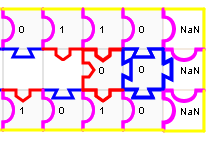
On constate que le bord gauche est rouge, ce qui veut dire que maintenant il y a une retenue.
La pièce à poser ensuite est la quatrième :

Encore une retenue :

Et encore une :
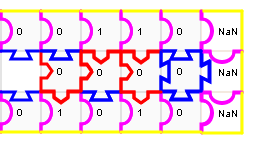
La somme s’écrit 10000 en binaire, ce qui veut dire que 6+10=16 :
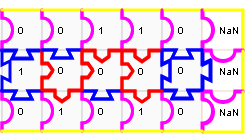
Soustraction binaire
Comme la pascaline, le puzzle additionneur peut servir à effectuer des soustractions. Par exemple pour effectuer 10-3 on s’arrange pour représenter 10 (1010 en binaire) dans la rangée du milieu, et 3 (11 en binaire) dans la rangée du bas. Seulement si on veut représenter le 0 final de 1010 au milieu, laquelle des deux versions suivantes choisir ?
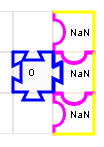
|
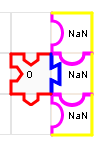
|
Pour le savoir, l’astuce qui marche est de commencer par poser 3 (soit 0011) en bas, avant de poser 10 (soit 1010). En posant 3 :
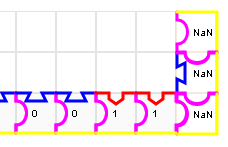
on voit que maintenant seul le second 0 convient pour le chiffre des unités de 1010 :

On peut maintenant poser 10 (soit 1010) :
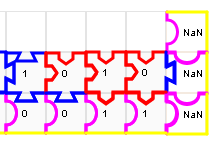
Si on complète le puzzle, on obtient en haut le seul nombre qui, additionné à 3, donne 10 :
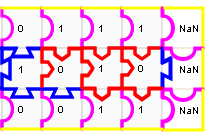
Pour le fun, essayer de calculer avec ce puzzle
-
- 10-10
- 3-10 (très intéressant : Si vous avez réussi le puzzle, vous avez inventé le complément à deux...)
Le principe des pavages de Wang
Wang s’est rendu compte, en rédigeant les étapes d’un raisonnement logique, que, lors de chaque étape du raisonnement, il se passe deux choses :
- La mémoire de travail du logicien change d’état ;
- le symbole que le logicien vient de lire peut être effacé et remplacé par un autre.
On peut donc représenter ces deux transformations par un pavé carré de cette manière :
| - | - | - |
| ancien symbole | ||
| ancien état | nouvel état | |
| nouveau symbole |
Voici le principe permettant de trouver quoi mettre à la droite de ce dessin :
L’ancien état de la nouvelle étape doit coïncider avec le nouvel état de l’ancienne étape
Un principe similaire pour les symboles a amené Wang à inventer une généralisation bidimensionnelle du jeu de dominos, avec appariements des chiffres. Puis avec ses étudiants ils sont passés à
- un appariement de couleurs : pavages de Wang
- un appariement de formes : puzzles de Wang.
L’ordinateur à ADN
Ce jeu de puzzle a des pièces en forme de croix. En effet lorsqu’on synthétise des nanomolécules d’ADN elles tendent à prendre cette forme. Leonard Adleman a eu l’idée de réaliser des puzzles calculateurs dont les pièces sont de telles nanomolécules, et de construire ainsi un ordinateur à ADN. Ce genre de puzzles « autoassembleurs » est adéquat pour étudier des problèmes NP par calcul massivement parallèle. Mais avec plusieurs heures de « calcul » (en fait des réactions chimiques) pour avoir la table des racines carrées entières des nombres à un chiffre, l’ordinateur à silicium a encore de beaux jours devant lui...
Pour en savoir plus, ne pas hésiter à parcourir l’article original qui comprend, outre d’autres puzzles, des simulations de machines de Post.


Commentaires