Voici les sujets :
| Sujet 1 | Sujet 2 | Sujet 3 |
|
|
|
Comme une bonne partie des sujets portait sur les partitions et leur représentation sous forme de forêts, voici des modules qui peuvent servir à manipuler les partitions et les dessiner :
| la classe Partition | le dessin d’une partition |
|
|
Le dessin des partitions utilise PyGraph.
Sujet 1 : blocs et ponts
Le sujet (partie II) propose de représenter des graphes non orientés par des structures Union-Find, elles-mêmes représentées par des forêts (dont les arbres sont orientés). Vous trouverez cette partie avec des dessins de forêts ici : blocs et ponts
Sujet 2 : expressions régulières et automates
Plan
Le sujet portait sur l’égalité des langages. Pour cela, l’algorithme proposé consistait à
- coder, pour chacun des langages à comparer, sa Regex) (et la dessiner, sous forme d’un arbre syntaxique),
- calculer, pour chacun des langages à comparer, un automate le reconnaissant, par la construction de Glushkov (présente dans le programme de MPI sous le nom d’algorithme de Berry-Sethi),
- rendre les automates déterministes et le minimiser, à l’aide de la relation d’équivalence de Nerode,
- comparer les automates minimaux obtenus : ils sont égaux si et seulement si les langages sont équivalents.
Comme la relation de Nerode est une relation d’équivalence, la structure union-find permet de rendre les algorithmes plus efficaces. Néanmoins, ici, on ne traitera pas de la question de l’efficacité.
Arbres
Dans la question 14, on demandait le dessin de la Regex (a+b)*a+(ab+ε)(c+ε) sous la forme d’un arbre binaire. Le voici :
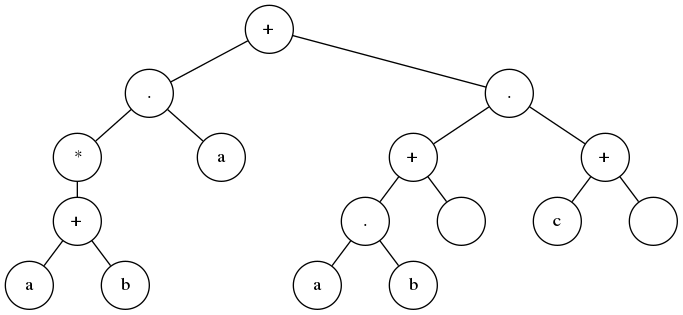
Dans la question 15, on demandait une fonction Python donnant la Regex à partir de sa représentation en arbre préfixe. Cette fonction se trouve dans le module glushkov.py que voici :
pour traiter l’exemple, il suffit de faire
from glushkov import *
exp = ['+',['*',['.',['a'],['b']]],['+',['.',['a'],['a']],['']]]
print(expression(exp))Dans la question 16 on demandait l’écriture d’une fonction Python permettant de savoir si une Regex contient le mot vide. Cette fonction figure également dans la module glushkov.py ci-dessus. Par exemple avec
from glushkov import *
exp = ['+',['*',['.',['a'],['b']]],['+',['.',['a'],['a']],['']]]
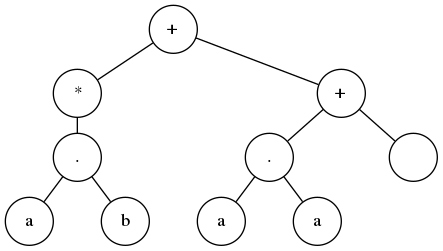
print(contient_le_mot_vide(exp))on a la réponse True puisque cette Regex contient le mot vide : on le voit sur son arbre syntaxique sous la forme d’une feuille vide en bas à droite :
Glushkov
Victor Glushkov (et après lui, Gérard Berry et Ravi Sethi) a trouvé un algorithme permettant, à partir d’une Regex linéaire, de fabriquer un automate la reconnaissant. Une Regex est dite linéaire si aucune lettre n’y apparaît plus d’une fois.
La question 17 demandait une fonction Python qui, à partir d’une Regex, donnait sa linéarisée. Cette fonction se trouve dans le module glushkov.py ci-dessous :
En entrant
from glushkov import *
exp = ['+',['*',['.',['a'],['b']]],['+',['.',['a'],['a']],['']]]
print(linearisation(exp))on a
['+',['*',['.',['a1'],['b2']]],['+',['.',['a3'],['a4']],['']]]
La construction de Gluskov utilise des ensembles :
- First est l’ensemble des lettres apparaissant au début de la Regex considérée.
- Last est l’ensemble des lettres apparaissant en de la Regex considérée.
- Follow est l’ensemble des couples de lettres successives dans au moins un des mots de la Regex considérée.
Le sujet utilise une classe spécifique Set pour les ensembles. Elle est dotée, en plus de la méthode de réunion (qui est lente), d’une méthode de réunion disjointe (qui est rapide, grâce à la compression des chemins permise par la structure Union-Find - voir plus loin). Comme ici on ne cherche pas un corrigé exhaustif, le module glushkov utilise les ensembles de Python, et non le module spécial du sujet.
Pour obtenir les enembles ci-dessus, avec la Regex linéarisée, on peut faire
from glushkov import *
exp = ['+', ['*', ['.',['a1'],['b2']]], ['.',['a3'],['a4']]]
first,last,null,follow = glushkov(exp)
print(first,last,null,follow)ce qui répond à la question 23 :
-
first==set(['a1', 'a3']) -
last==set(['a4', 'b2']) -
follow==set([('a1', 'b2'), ('a3', 'a4'), ('b2', 'a1')])
La question 24 demandait quel type de parcours est effectué sur l’arbre syntaxique de la Regex, pour construire son automate de Glushkov. On voit sur le code source qu’il s’agit d’un parcours suffixe.
Une fois qu’on a les ensembles First, Last et Follow et qu’on sait si la Regex contient le mot vide, on peut dessiner un graphe orienté représentant la relation Follow. Les états finaux sont dans Last et les arêtes issues de l’état initial sont dans First. Il suffit alors de délinéariser (enlever les chiffres qui avaient été ajoutés lors de la linéarisation) pour avoir l’automate de Glushkov de la Regex. Celui de la Regex considérée est :
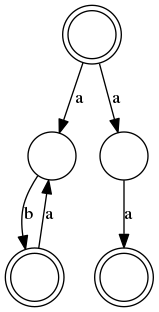
Pour obtenir ce genre de graphe il faut installer le module graphviz, décommenter la première ligne du module glushkov et utiliser la fonction automate sur les données first, last, null et follow obtenues en lançant la fonction glushkov sur l’automate linéarisé.
L’automate de Glushkov reconnaît bien la Regex considérée mais il n’est pas déterministe : la lecture du premier a peut le faire aller dans un des deux états non terminaux (cercles simples) mais comment savoir lequel ? En 1959, Michael Rabin et [Dana Scott] ont publié un algorithme permettant, à partir d’un automate comme celui ci-dessus, de trouver un automate déterministe reconnaissant le même langage. Appliqué à l’automate non déterministe ci-dessus, il donne
(l’état initial est à droite)
La construction de Rabin et Scott consiste à considérer comme états du nouvel automate, des ensembles d’états de l’ancien automate : on l’appelle donc construction par sous-ensembles.
Dans la suite, les automates sont supposés déterministes et complets (pour chaque état de l’automate et chaque lettre de l’alphabet il y a une transition). Le problème de comparer deux Regex revient donc à celui de trouver l’automate le plus petit possible (ayant le moins d’états) reconnaissant une Regex. Ensuite il suffira de comparer les automates minimaux des deux Regex pour savoir si elles sont égales.
Pour trouver l’automate minimal, on partitionne les états d’un automate : les états de l’automate minimal sont des partitions d’états de l’ancien automate.
Partitions
La structure Union-Find (voir onglet suivant) permet de simplifier une partition en réduisant le nombre de classes d’équivalence (opération union). Dans cette partie, on fait le contraire : raffinement de partition. En partant de cette partition :
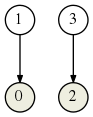
l’automate
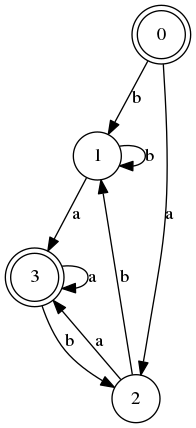
produit la nouvelle partition :
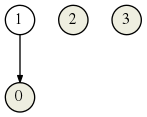
En effet alors qu’initialement 2 et 3 étaient dans la même classe d’équivalence, la lettre b les envoie respectivement sur 1 et 2 qui n’étaient pas initialement reliés.
Un automate a donc un effet sur une partition : il la raffine. Il s’agit là d’un processus d’apprentissage.
Les réponses aux questions 35 et 36 figurent dans le fichier Python ci-dessous :
Il utilise les modules suivants :
| partitions | PyGraph | dessin de partitions |
|
|
|
|
On constate que le choix a été fait de modéliser un automate par un tuple. Définir une classe Automate() n’aurait pas été moins judicieux. Cette construction est laissée en exercice.
Dans la suite, les lettres de l’alphabet sont numérotées et donc représentées par des entiers. L’état 0 et la lettre 0 ne sont pas à confondre évidemment. Avec ce nouveau codage, l’automate ci-dessus devient
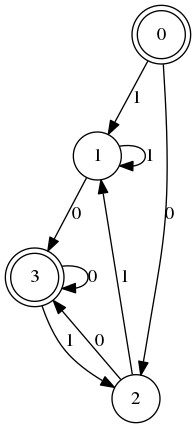
Nerode
Les dessins d’automate montrent deux sortes de sommets :
- les doubles cercles sont des états finaux (ou accepteurs)
- les simples cercles ne sont pas accepteurs.
Cela constitue une partition appelée de Nerode. Elle est calculée par la fonction calcule_partition0() qui est dans le fichier ci-dessous :
Appliquée à un automate, elle donne une partition au sens du module partitions donné au début de cet article. Et on peut dessiner cette partition.
Avec l’automate
on obtient cette partition de Nerode :
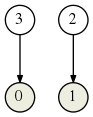
En effet 0 et 3 (classe de représentant 0) sont les deux états terminaux de cet automate, alors que 1 et 2 (de représentant 1) ne le sont pas.
En 1956, Moore a trouvé un moyen de construire l’automate minimal à partir de l’automate A. Sa construction passe par un raffinement de partitions, en commençant par la partition de Nerode de A :
puis en affinant cette partition avec A :
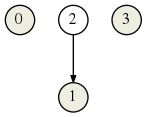
Et ainsi de suite, par affinements successifs. En afinant à l’aide de A la partition ci-dessus, on trouve
ce qui montre que l’algorithme est terminé à ce stade.
La fonction moore(A) est dans le fichier
On l’utilise comme ceci :
from partitions import *
import viz_partition as vp
from raffinement import *
delta = [[2,1],[3,1],[3,1],[3,2]]
F = [0,3]
A = (2,4,delta,0,F)
graphe = vp.VizPartition(moore(A))
graphe.png('moore')ce qui produit ce dessin de partition :
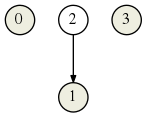
Les états 1 et 2 étant équivalents, leur classe (de représentant 1) sera un seul état de l’automate minimal. L’idée est de ne pas distinguer les états équivalents : l’automate miniml est le quotient de l’automate A par la relation d’équivalence de Nerode.
Dans le cas présent le quotient est cet automate :
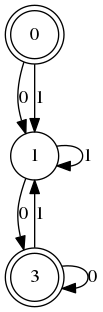
égalité
Une fois qu’on sait trouver l’automate minimal d’une Regex, on peut comparer des Regex en cherchant un éventuel isomorphisme entre leurs automates minimaux respectifs.
La structure Union-Find permet de comparer directement deux Regex sans passer par leurs automates de Nerode. Cette fonction est proposée dans l’énoncé (ici, légèrement modifiée pour être utilisable avec le module partitions.py) :
from partitions import *
def test_egalite_langages(A,B):
mA,nA,deltaA,iA,FA = A
mB,nB,deltaB,iB,FB = B
assert mA==mB
partition = Partition(nA+nB)
a_faire = [(iA,iB)]
while len(a_faire):
p,q = a_faire.pop()
if partition.find(p) != partition.find(q+nA):
if FA[p] != FB[q]:
return False
else:
partition.union(p,q+nA)
for a in range(mA):
a_faire.append((deltaA[p][a],deltaB[q][a]))
return TrueMais si on essaye de l’utiliser pour vérifier que l’automate minimal vu dans l’onglet précédent vérifie le même langage que l’automate A :
A = (2,4,[[2,1],[3,1],[3,1],[3,2]],0,[0,3])
B = (2,3,[[1,1],[2,1],[2,1]],0,[0,2])
print(test_egalite_langages(A,B))on a la réponse False parce que les listes d’états finaux ne sont pas les mêmes pour les deux automates : l’état 3 est final pour le premier automate mais n’existe même pas pour le second !
Sujet 3 étude de cas : tournées de véhicules
On s’intéresse à la partie I et plus précisément aux sept premières questions qui manipulent des graphes pondérés. On y retrouve des calculs simples et moins simples : matrices d’adjacence, plus courtes distances (algorithme de Floyd-Warshall), optimisation de tournées (algorithme de Clarke et Wright pour le problème de tournées de véhicules).
Les matrices d’adjacence et l’algorithme de Floyd-Warshall sont au programme d’informatique de la classe MP2I [1] ; et en Tle NSI, ces algorithmes peuvent servir de support pour des exercices guidés ou des mini-projets. Avant cela, on peut imaginer des activités débranchées qui restent (en avril 2023) à tester...
Le corrigé de cette partie est ici : Étude de cas
Sujet 3 fondements : réseaux de neurones
Plan
Dans la première partie, on modélise un neurone et on étudie les fonctions booléennes calculables par ce neurone.
Dans la seconde partie, on relie des neurones entre eux pour obtenir un réseau de neurones.
Dans la partie III, on étudie l’apprentissage du réseau.
Ensuite on étudie les réseaux de neurones récurrents et on fait le lien avec les automates, et enfin on étudie d’autres fonctions d’activation, qui ne sont pas discrètes.
ReLU
Le sujet aborde plusieurs fonctions d’activation des neurones, qui sont aisément définissables en Python :
def H(x):
return int(x>=0)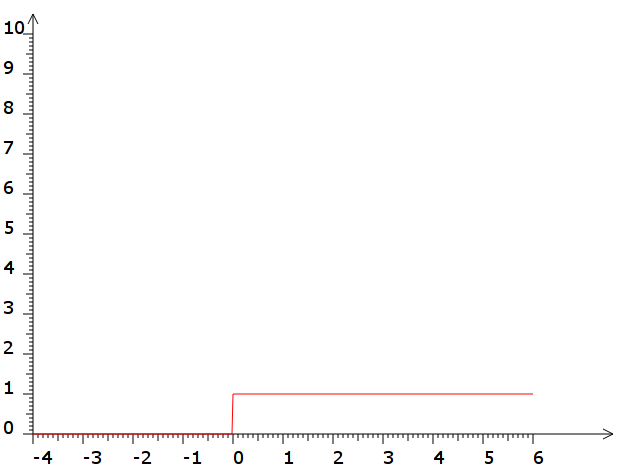
- la fonction ReLU :
def ReLU(x):
return max(x,0)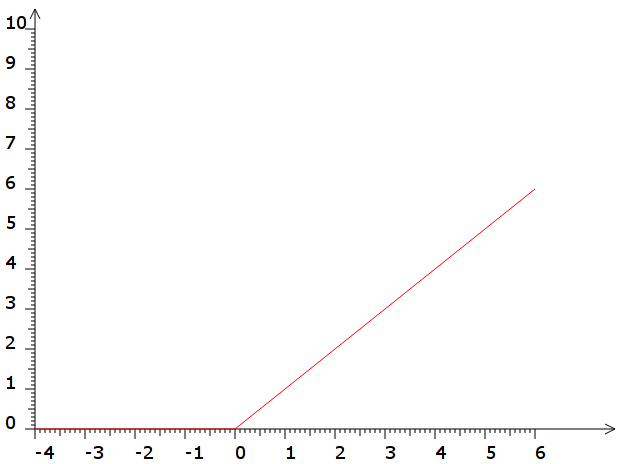
- la sigmoïde idéale :
def s(x):
return min(ReLU(x),1)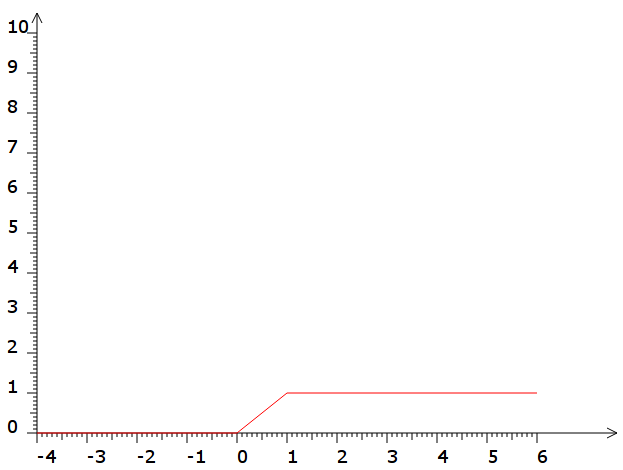
Dans le début du problème, seule la fonction de Heaviside est utilisée.
neurone
- La fonction logique NOT peut être calculée par un neurone de poids -1 et de seuil 0.
- La fonction logique AND peut être calculée par un neurone à seuil, car il est possible de séparer les points bleus (valeur booléenne 0) et rouge (valeur booléenne 1) par une droite représentant le seuil (son équation est de la forme x+y=seuil) :
Une représentation possible est (1,1,2) (poids 1 et 1, seuil 2). Plus généralement avec des poids 1 et un seuil égal au nombre d’entrée, AND à n entrées est calculable par un neurone. Et le vote majoritaire est calculable de façon similaire avec un seuil égal à la moitié du nombre d’entrées (et les poids égaux à 1).
- La fonction OR peut aussi être calculée par un neurone à seuil, parce que là aussi on peut séparer les points bleu et rouges par une droite :
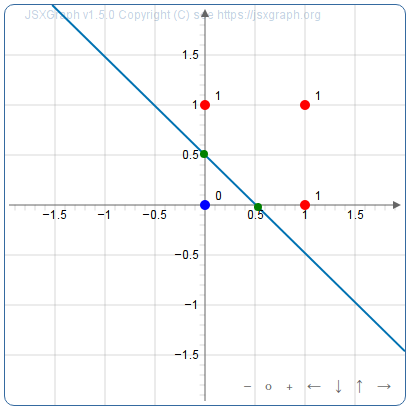
On lit la représentation (1,1,1) soit les poids 1 et 1 et le seuil 1. Plus généralement la fonction OR à n entrées est calculable par un neurone à seuil.
- mais la fonction XOR peut être représentée par un neurone à seuil, si et seulement s’il est possible de séparer les points bleus et rouges par une droite (verte, on peut bouger les points la définissant pour essayer) :
Si vous y êtes arrivés, c’est que la fonction XOR peut être calculée par un neurone à seuil, et les poids de ce neurone, ainsi que son seuil, sont lisibles sur la figure. Si vous n’y êtes pas arrivés, c’est que le problème n’a pas de solution...
De même, la fonction parité (le nombre d’entrées égales à 1, modulo 2) n’est pas calculable par un neurone à seuil.
apprentissage
Au lieu de comparer la somme pondérée des entrées avec le seuil, on va comparer avec 0 (seuil nul) la différence entre les entrées pondérées et le seuil. En plus, on remplace la sortie 0 par -1. Pour la porte OR, les données d’apprentissage sont donc
0 0 -1
0 1 1
1 0 1
1 1 1(la troisième colonne est le seuil)
Chaque fois que la somme pondérée est positive ou nulle, on dit qu’il y a une erreur d’apprentissage. Dans ce cas, on soustrait la donnée d’apprentissage ayant causé l’erreur aux poids actuels. La condition d’arrêt est que plus aucune donnée na causé d’erreur d’apprentissage durant le passage dans la boucle.
Pour OR, voici les états successifs des données d’apprentissage :
réseau
On a vu précédemment que la fonction XOR n’est pas calculable par un neurone à seuil. Mais elle l’est par un réseau de neurones à 2 couches :
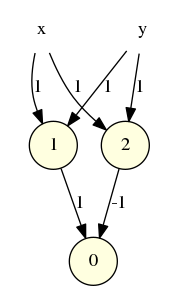
Le neurone de seuil 1 est un OR : il n’est inactif que si les deux entrées sont à 0. Le neurone de seuil 2 est un AND : il n’est actif que si les deux entrées sont à 1. La fonction XOR sera donc réalisée si le premier neurone est actif mais pas le second. On donne donc un poids -1 au AND et un poids 1 au OR pour isoler cette situation où une seule entrée est active.
Une autre façon de faire est généralisable (par exemple pour prouver que la parité sur n entrées - XOR étant la parité sur 2 entrées - est calculable par un réseau de neurones à 2 couches). Elle consiste à utiliser un neurone pour détecter chaque jeu d’entrées possible :
- Pour savoir si aucune entrée n’est active, il suffit de prendre un neurone OR et de nier sa sortie :
Le neurone aura donc un seuil de -0,5 et ses poids seront -1 et -1.
- Pour savoir si les deux entrées sont actives, il suffit de prendre un neurone AND :
Le neurone aura donc pour seuil 1,5 et pour poids 1 et 1.
- Pour savoir si seule l’entrée x est active, on peut isoler le point en rouge ci-dessous :
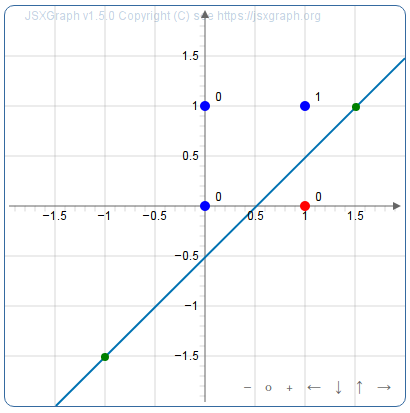
Le neurone aura donc pour seuil 0,5 et pour poids 1 (pour x) et -1 (pour y)
- Pour savoir si seule l’entrée y est active, on peut isoler le point en rouge ci-dessous :
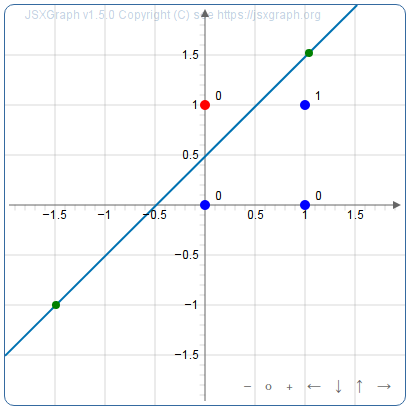
Le neurone aura donc pour seuil 0,5 aussi mais pour poids -1 (pour x) et 1 (pour y).
Une couche formée de ces 4 neurones aura donc pour propriété qu’un seul des 4 sera actif. Si c’est un de ceux dont le poids est 0,5 alors c’est qu’on a une des entrées (0,1) ou (1,0) et il suffit de regrouper les sorties des deux neurones de seuil 0,5 (dont un seul sera actif) par un neurone OR pour avoir un réseau de neurones réalisant XOR :
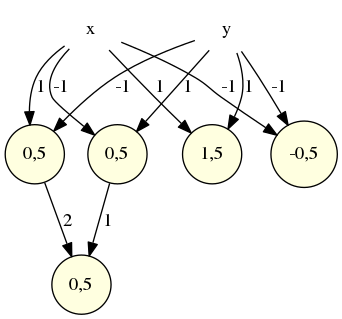
Cette technique (une couche séparant les cas possibles pour les entrées) est utilisée pour réaliser la fonction de transition d’un automate et ainsi, simuler un automate par un réseau de neurones récurrent. C’est ainsi que Kleene a défini les automates dans son article de 1951.
registres
Les questions 38 à 42 montrent un résultat intéressant : on peut
- simuler un réseau de neurones ReLU dans une machine à registres
- réaliser une machine à registres avec un réseau de neurones ReLU.
Ce résultat est intéressant parce que les machines à registres ont la même puissance de calcul que les machines de Turing (du moins si les registres sont illimités).
Dans la question 38, on demandait un programme ne faisant appel qu’à des incrémentations, décrémentations et tests de nullité, permettant de doubler une variable. Avec un graphe de flot de contrôle, on peut le faire avec 2 registres seulement :
La question 39 semble comporter une erreur : il est dit que r est réel, mais r est le contenu d’un registre (donc un entier naturel a priori). On va donc représenter graphiquement les données sous forme de nuages de points.
- Pour la fonction r+1 (incrémentation du registre) on prend un seuil égal à -1 :
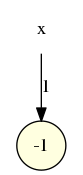
qui représente graphiquement la fonction r+1 :
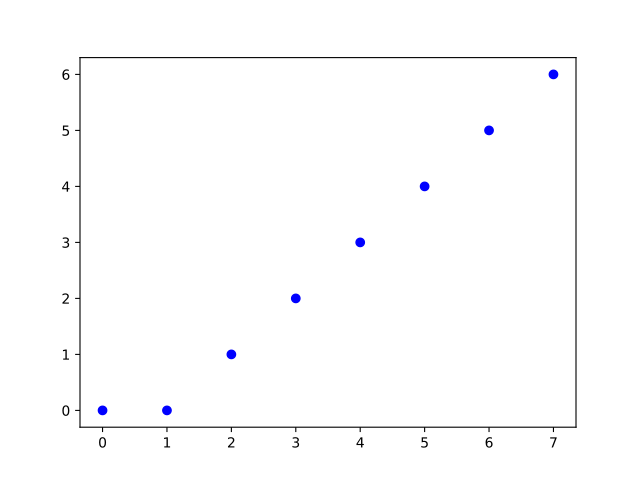
- Pour la fonction max(0,r-1) (ou décrémentation si possible du registre) il suffit de prendre un seuil égal à 1 :
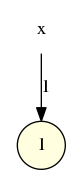
qui représente graphiquement la fonction égale à r-1 si r-1 est positif ou nul :
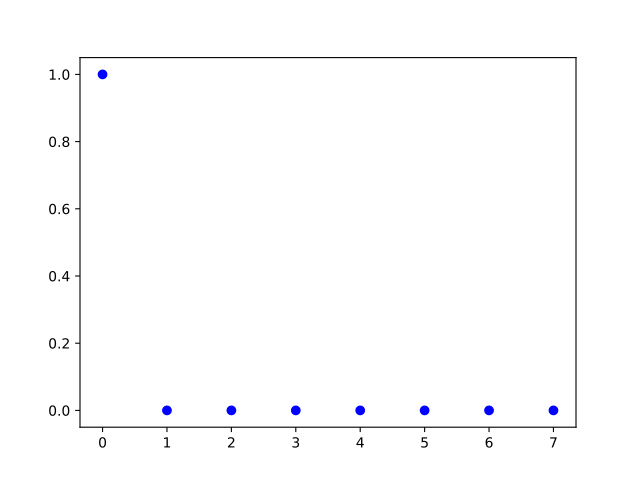
- Pour la détection de 0 (fonction qui vaut 1 si r=0, 0 sinon) voici une solution avec 3 neurones organisés en deux couche :
En effet la représentation graphique de la sortie du réseau correspond au cahier des charges :
Mais voici également une solution avec un seul neurone :
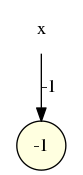
pile
Toute chaîne de caractères 0 et 1 peut être représentée par un réel compris entre 0 et 1 (0 représenté par 1 en base 4, 1 représenté par 3 en base 4). Cela permet de simuler les empilements et dépilements de 0 et de 1 par des fonctions sur les flottants. Voici un simulateur de ce pile basé sur ce principe :
L’ensemble triadique de Cantor permet aussi de repsrésenter les chaînes de caractères 0 et 1, mais avec la base 4 on a de la marge pour séparer les 0 des 1. Avec ça,
- La fonction top permettant de connaître le dessus de la pile sans modifier celle-ci, est calculable par ce neurone :
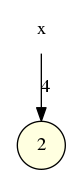
- La fonction push(0) est représentable par ce neurone :
- La fonction push(1) est représentable par ce neurone :
Annexe : documents historiques
L’article d’Edward Moore en 1956 (notion d’automate de Moore évoquée dans le sujet 1, et algorithme du sujet 2 pour avoir l’automate minimal) :
La théorie des automates selon Rabin et Scott en 1959 (Nerode y est cité) :
La description de l’algorithme de Floyd-Warshall, par Warshall en 1961 :
Le même algorithme, décrit par Floyd en 1962 :
L’algorithme de Clarke et Wright, en 1964 :
La naissance de la structure Union-Find en 1964 :
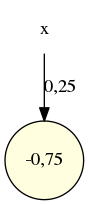
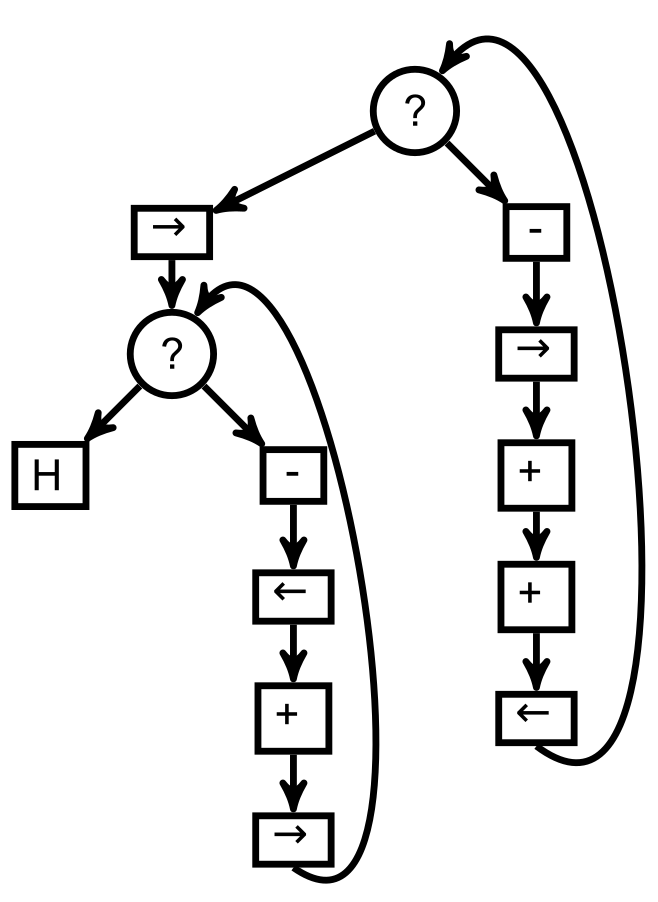
Commentaires