Le problème avec Python est qu’une telle fonction existe déjà, par exemple on peut faire
from math import pi
print(round(pi,2))Pour permettre aux élèves de choisir quand même Python, il leur a donc été demandé plutôt de créer une fonction tronc2 qui, au lieu de l’arrondi à deux chiffres, donne la troncature :
Du coup, l’interdiction d’utiliser la calculatrice était une erreur, puisque si la calculatrice affiche les arrondis à deux chiffres, elle ne le fait pas pour les troncatures.
Le programme d’algorithmique de Première (« objectifs pour le lycée ») commence par
Instructions élémentaires (affectation, calcul, entrée, sortie)
et donne pour exigibles, entre autres :
- d’écrire un programme calculant et donnant la valeur d’une fonction ;
- ainsi que les instructions d’entrées et sorties nécessaires au traitement.
En plus, l’écriture de l’algorithme comme une fonction (avec une entrée et une sortie) présente l’avantage de faciliter le test de l’algorithme en appliquant (« map ») la fonction à une liste d’antécédents :
list(map(tronc2,[13*n/7 for n in range(5)]))L’impossibilité de définir algorithmiquement une fonction avec Algobox est, de ce point de vue, une gêne ; cependant, tous les élèves ont eu des difficultés à comprendre que le « résultat » de l’algorithme doit être dépendant de son « entrée », que celle-ci soit imposée au moment du test de l’algorithme (Algobox et la calculatrice), ou par un appel à une fonction définie préalablement (Python et JavaScript). Une solution à ce problème pourraît être l’engagement direct permis par le tableur et son langage « BASIC »...
Des difficultés imprévues sont vite apparues :
Sous Algobox, c’est le test de l’algorithme qui effraye un peu au début, comme en témoignent ces erreurs d’élèves :
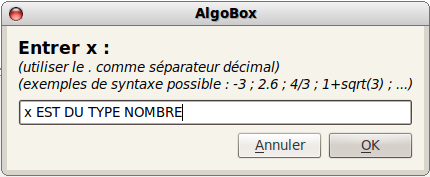
Sous Python, c’est la nécessaire rigueur de la syntaxe qui déroute (ici il fallait ajouter une ligne vide pour finir la définition de la fonction, et utiliser « print » en mode interactif) :
Les élèves ont besoin de se familiariser avec l’outil [1] et ont donc d’abord testé ledit outil (ou plusieurs d’entre eux parfois) avec les fonctions identité et constantes (comme on le voit ci-dessus avec l’exemple Python).
Seuls les meilleurs élèves [2] ont pensé à la fonction partie entière, sans toutefois réussir à trouver comment la modifier pour arriver à deux décimales. La difficulté du problème, déjà constatée lors de ce TP de fin d’année, semble se confirmer là aussi.
Moins de la moitié est partie sur une idée spontanée et assez intéressante : Essayer d’élever x à la puissance 2 ou -2 [3].
Vers une évaluation par compétences
Les compétences visées étaient
- la capacité à démarrer l’ordinateur et le logiciel (2 points)
- l’entrée d’une donnée numérique (2 points)
- l’affichage ou la sortie du résultat du calcul (2 points)
- la capacité à tester l’algorithme (2 points)
- penser à utiliser la troncature entière (4 points)
- penser à la multiplication par 100 (4 points)
- penser à la division (4 points)
Ce qui donne une note sur 20, dont voici le diagramme en bâtons :
Avec une moyenne de 8,5 ce TP n’est pas vraiment « réussi » mais en écoutant les élèves, on se rend compte que la notion de fonction, bien qu’évaluée au DNB, est très peu maîtrisée en entrant en Seconde [4].
Exercice d’arithmétique :
Sachant qu’il faut 5 secondes de moins pour lire un algorithme Python que pour lire un algorithme écrit dans un autre langage que Python, et qu’un prof est amené à lire en moyenne 5 fois l’algorithme de chaque élève au cours du TP, combien de temps gagne-t-il pour évaluer une classe de 36 élèves au cours du TP ?
Le fait que la moitié des élèves ait choisi Python, n’est donc peut-être pas totalement étranger à la possibilité de remplir la grille d’évaluation par compétences au cours du TP, et donc que les élèves aient leur note dès la fin de celui-ci...
Commentaires