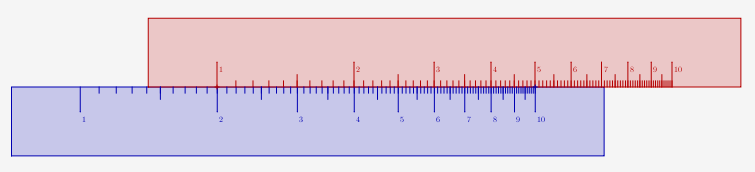
Règle à calcul traditionnelle
Comme une composée de translations de vecteurs colinéaires matérialise une addition de réels, faire coulisser deux règles graduées logarithmiquement permet de calculer graphiquement des produits de nombres positifs :
Pour calculer le produit $12 \times 13$, on estime mentalement (sans la règle) son ordre de grandeur ($10 \times 10 =100$) ce qui ramène à la multiplication $1,2 \times 1,3$ qui sera à la fin multiplié par 100. Ensuite on place l’origine de la règle mobile (en rouge) sur la graduation 1,2 et en face du 1,3 rouge on voit environ 1,55. D’où le produit (après multiplication par 100) $12\times 13 \simeq 155$. Ce qui révèle que, comme tous les instruments de calcul graphique, la règle à calcul est à la fois plus rapide et moins précise que la calculatrice [1].
Par contre pour calculer $8 \times 7$ on a un problème : Une fois la graduation 1 rouge mise face au 8 bleu, la règle rouge est presque entièrement en-dehors de la figure et il devient impossible de lire ce qui est en face de la graduation 7 rouge. Une solution serait de doubler l’une des règles en longueur comme c’est fait dans cet article. Une autre est de "remplacer 1 par 10" : On fait glisser la règle rouge vers la gauche pour que le 8 bleu soit non plus en face du 1 rouge mais en face du 10 rouge. Alors en face du 7 rouge on voit en bleu un 5,6 bleu ce qui veut dire que $0,8 \times 7=5,6$ ce qui revient bien à $8 \times 7=56$, ce que n’importe quel collégien connaissant ses tables de multiplication par cœur sait très bien [2].
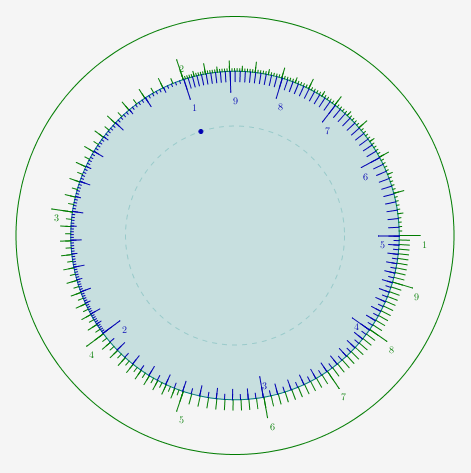
Cercle à calcul
L’argument ci-dessus revient à raisonner modulo le logarithme de 10. Comme en plus l’addition de nombres modulo $2 \pi$ est matérialisée par la composée de deux rotations de même centre, les graduations logarithmiques sur un cercle donnent aussi une règle à calcul :
Choisir entre les deux est essentiellement une question d’esthétique. On constate dans ce musée que de façon générale, le choix est rarement en faveur du cercle...

Commentaires