Pour Édouard Lucas, le jeu de taquin généralisé (qu’il appelle continental parce qu’il y a des continents et des presqu’îles servant de garages) est un jeu sérieux sur la théorie de Galois, à en juger par cette description :

Découvrir les groupes de permutation et leur énervante non-commutativité en jouant avec des cartes ? Pourquoi pas ? On va essayer, mais en s’aidant du logiciel GAP qui est spécialisé dans la théorie des groupes finis.
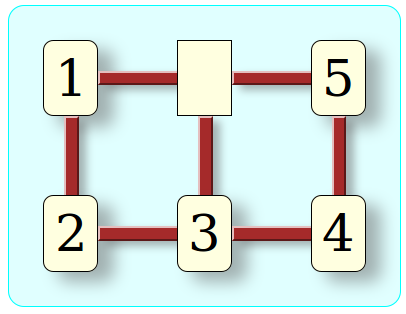
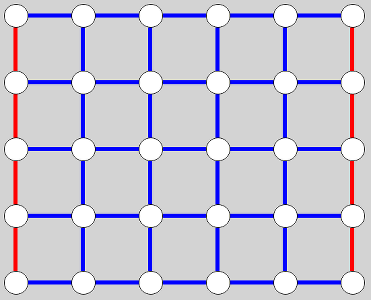
On va commencer par un exemple simple, un jeu de taquin à 3×2 cases (au lieu du 4×4 classique), la case vide étant initialement au milieu de la rangée du haut :
Il s’agit d’un jeu en ligne, que l’on peut ouvrir dans le navigateur pour y jouer un peu. Le plateau de jeu représente un étang surmonté de pontons que l’on emprunte pour déplacer les cartes.
Les 6 risqués de Ricky
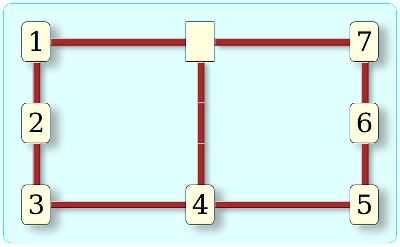
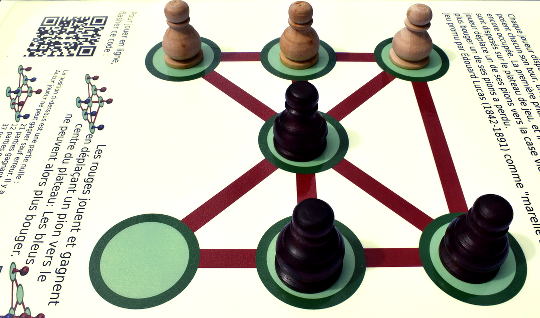
Ce jeu a été nommé par Conway, en hommage à Richard Wilson, qui est l’auteur du résultat sur le lien entre graphes bipartites et nombre de permutations, et de cette variante où il y a 120 permutations sur les 720 permutations des 6 cartes laissant vide le garage central :
Si on mélange totalement au hasard les cartes, on a donc une chance sur 6 de pouvoir résoudre le jeu, d’où le nom de « risqué ».
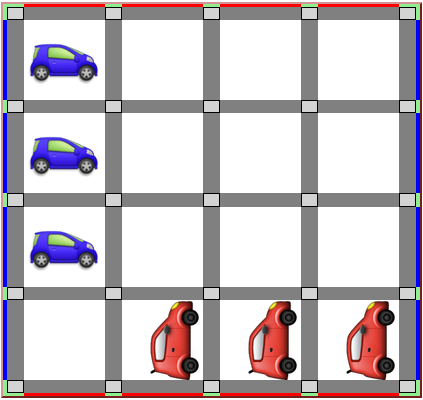
Après avoir dangeureusement transporté des cartes numérotées sur des pontons au-dessus du marais, voici un autre jeu où il est question de mangroves, à terraformer. Au départ du jeu il y a des toutes petites rivières allant d’un bord à l’autre (une seule carte, par exemple le coin en bas à droite), et des petites rivières n’occupant que deux cartes. Le premier joueur qui complète une rivière d’au moins trois cartes allant d’un bord à un bord, a gagné :
Après expérimentation de ce jeu, il apparaît nécessaire de rajouter une règle pour éviter les parties nulles : Ne pas jouer la carte qui vient d’être jouée...
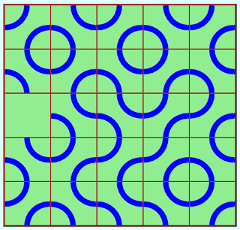
Ce jeu a été créé par Lewthwaite, qui est également l’auteur de cette variante :
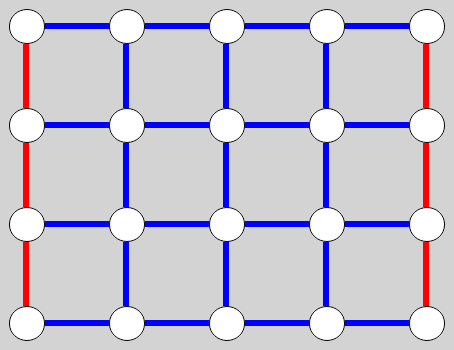
Pour cette version, Berlekamp, Conway et Guy ont trouvé une stratégie gagnante (pour le second joueur) basée sur un pavage des 24 cases non centrales par des dominos.
Bonus :
Pour jouer au jeu « lucky seven » sur Android, voici un installeur :








Commentaires