La suite logistique Un+1 = r Un (1-Un)

Cette suite est, à l’origine, une modélisation de la croissance et de la décroissance des populations animales au cours du temps. La légende nous parle de l’étude de la reproduction de mignons lapins :

L’idée c’est de définir r comme le taux de croissance de la population. Par exemple, si r=2 alors la population double chaque année. Ce facteur r Un, correspond à une suite géométrique classique, ce qui veut dire que pour r=2, la population va exploser très rapidement.

Pour équilibrer cette croissance, il va falloir rajouter un facteur de mort, c’est à dire limiter la population. Cela arrive dans des environnements réels, que ce soit tous ces prédateurs qui dévorent nos pauvres lapins ou plus simplement le manque de ressources indispensables comme la nourriture ...

Le terme (1-Un) limite et normalise le résultat sous la forme du pourcentage actuel de la population maximale définie à 1 soit 100%.

Le professeur Robert M. May a popularisé cette équation dans la revue scientifique Nature dès 1976 en étudiant comment elle convergeait en fonction de son taux de croissance r. [1] [2].

L’article de cet illustre professeur sur lequel est basé mon travail est disponible à la lecture en anglais en cliquant ici.

Suivant les valeurs [3] du taux de croissance de la suite logistique, L’équation Un+1 = r Un (1-Un) génère une suite convergente, une suite soumise à oscillations ou une suite chaotique.

C’est la visualisation de cette évolution vers la complexité qui va nous intéresser dans la suite de l’article. [4]

Coder une visualisation de la suite logistique en Python

La première étape, c’est d’importer la librairie Python matplotlib pour tracer une courbe avec sa fonction plot :

import matplotlib.pyplot as plt

Puis on initialise les variables et on fabrique la fonction Un+1 = f(Un). [5]

nmax = 60   # C'est l'année calculée maximale
r = 2.7     # C'est le taux de croissance
u0 = 0.7    # C'est la population initiale en %

# C'est la suite Un définie récursivement
def u(n):
    u=u0
    for i in range(n):
        u=r*u*(1-u)
    return u

On en profite pour documenter notre graphique en identifiant ses axes et en lui donnant un titre ( Il est possible de s’inspirer de la syntaxe des formules LaTeX sous matplotlib pour générer de belles formules en l’insérant entre des $ ) :

title ="Suite logistique "+"$u_{n+1} ="+str(r)+"u_n (1-u_n)$"+" avec "+"$u_0 ="+str(u0)+"$"
plt.title(title)
plt.xlabel("n")
plt.ylabel("$u_n$")

Enfin, il suffit de calculer les valeurs des y=Un pour chaque x=n appartenant à l’intervalle [0,nmax] et générer la courbe puis afficher la fenêtre plplot :

# C'est ici qu'on calcule les valeurs de la suite
x = []
y = []
for n in range (0 ,nmax) :
    x.append(float(n))
    y.append(float(u(n)))

plt.plot(x,y,'bo')

# On affiche la fenêtre pltplot
plt.show()

Le code complet proposé ci-dessus est disponible en cliquant ici.

Étude expérimentale de la convergence de la suite logistique en fonction du taux de croissance r

Pour une valeur de r=2,7, on observe une convergence rapide vers une valeur qui reste identique quelque soit la valeur de U0

Pour une valeur de r=3,4, on observe une oscillation entre deux valeurs stables, là encore, quelque soit la valeur de U0

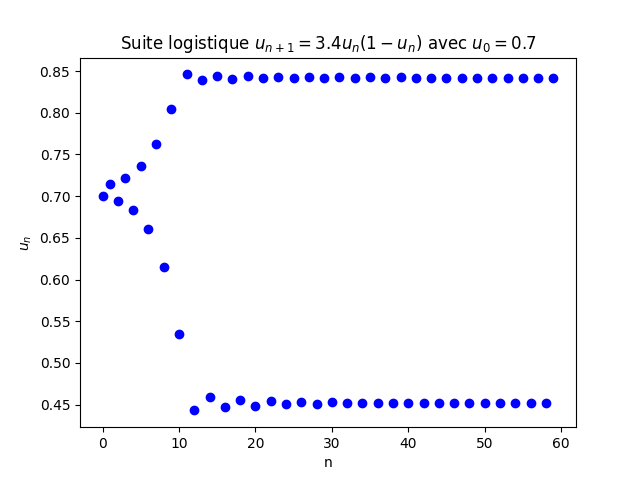
Pour une valeur de r=3,8, même en essayant des valeurs beaucoup plus élevées de n, on n’observe plus aucune forme de régularité : il n’y a plus que du chaos :

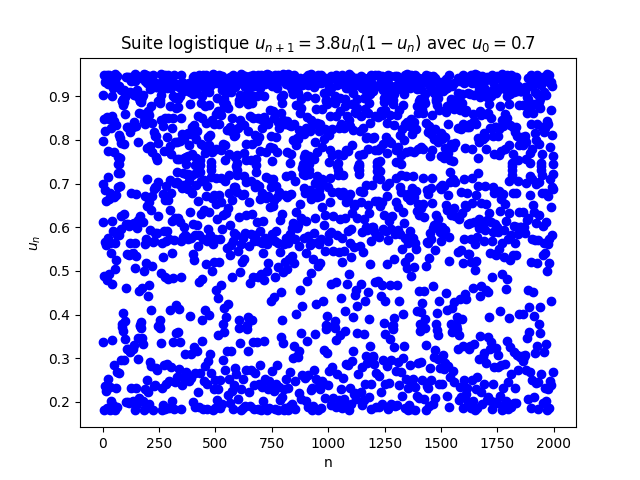
Pour pouvoir explorer le comportement de cette suite expérimentalement, il est possible de rajouter des curseurs pour pouvoir modifier interactivement les valeurs de r et de u0 et ainsi bénéficier d’une visualisation en temps réel.

Avec cette facilité de contrôle du taux de croissance r, on découvre qu’au milieu du chaos, il y a plusieurs zones où l’ordre revient comme par exemple pour r=3,831 où l’on observe des oscillations entre 3 valeurs stables :

Ce code complet comportant des curseurs est très agréable à manipuler, c’est un bon exemple d’utilisation des curseurs sous matplotlib et vous pouvez le télécharger et le tester dans votre interpréteur Python en cliquant ici.

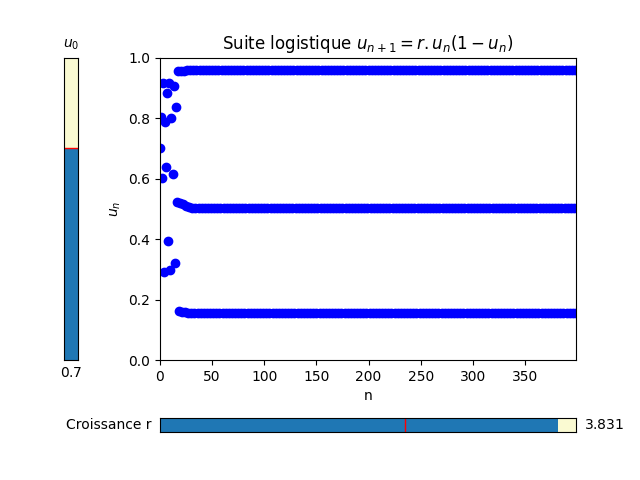
Coder le diagramme de bifurcation

Étant donné le comportement extrêmement complexe de la suite logistique, il est très intéressant de changer notre mode d’observation en générant un diagramme, c.a.d un nuage de points donnant les « multiples » valeurs possibles de Un en fonction du taux de croissance r.

Ce diagramme, décrit par le professeur Robert M. May dans ses articles sera nommé diagramme de bifurcation.

Pour commencer, on importe toujours la librairie Python matplotlib qui va nous servir cette fois-ci pour tracer un nuage de points soit la fonction scatter de plplot.

import matplotlib.pyplot as plt

Ensuite, nous allons initialiser toutes les variables indispensables pour pouvoir tracer notre diagramme :

nmin = 40     # Valeur minimale de n 
nmax = 200    # Valeur maximale de n
r = 1.0       # Le taux de croissance de départ
rmax = 4.0    # Le taux de croissance maximal
dr = 0.001   # La variation de r soit la capacité à zoomer dans le diagramme
u0 = 0.6      # La population initiale en %

La suite logistique va être définie sous la forme d’une fonction avec tous ses paramètres variables comme r et u0 [6] :

# C'est la suite Un définie récursivement
def u(n,r,u0):
    u=u0
    for i in range(n):
        u=r*u*(1-u)
    return u

Bien sûr, il est indispensable de commenter clairement les axes et le titre du diagramme de bifurcation :

title ="Diagramme de bifurcation de "+"$u_{n+1} = r.u_n (1-u_n)$"
plt.title(title)
plt.xlabel("r")
plt.ylabel("Valeurs de "+"$u_n$")

Le cœur du calcul (non optimisé) se trouve ici :
– On parcourt toutes les valeurs de r dans l’intervalle [1 ; 4[ en l’incrémentant par dr à chaque passage de la boucle while.
– Pour chaque valeur de r, on calcule les valeurs de Un dans l’intervalle [nmin ; nmax]

# C'est ici qu'on calcule les valeurs du diagramme de bifurcation
x = []
y = []
while r < rmax :
    for n in range (nmin ,nmax) :
        x.append(float(r))
        y.append(float(u(n,r,u0)))
    r=r+dr

Enfin, on génère le nuage de points avec la fonction scatter de plplot et on affiche la fenêtre plplot :

plt.scatter(x,y,1)
plt.show()

Le code proposé ci-dessus est disponible en version complète en cliquant ici.

Explorer expérimentalement le diagramme de bifurcation

Après des calculs plus ou moins longs en fonction de la puissance de votre ordinateur, on obtient le diagramme de bifurcation ci-dessous :

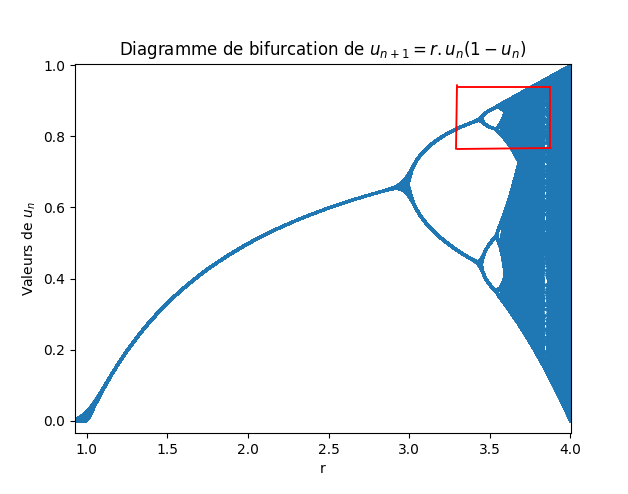
On remarque tout de suite qu’il ressemble fortement à une fractale car il semble que les bifurcations se répètent à l’identique avant de basculer dans le chaos. En diminuant la valeur de dr, on va très fortement augmenter le temps de calcul mais on pourra profiter des fonctions de zoom de plplot pour explorer la réalité de ce comportement fractal :

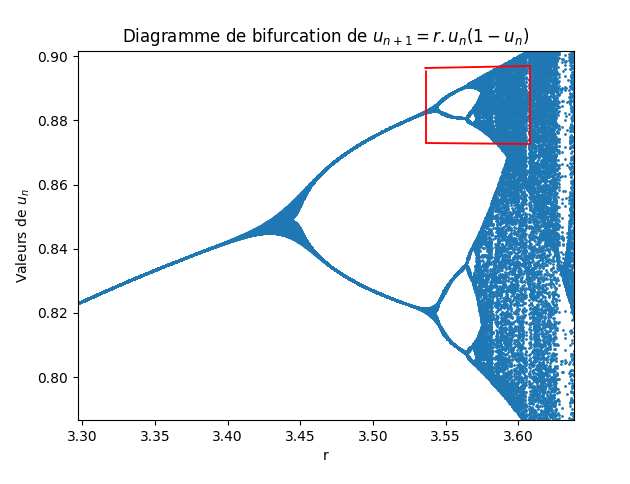
Si on zoome encore, il est clair que c’est effectivement une fractale. On arrive à la limite de résolution. (Ici pour une précision de zoom correspondant à un dr = 0.0005 ) :

Conclusion

Des équations très simples comme la suite logistique peuvent exhiber des comportements non-linéaires complexes.

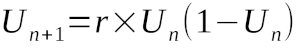
Il y a dans la simplicité, les germes de la complexité. Cette émergence du chaos au cœur d’une équation si simple ne cessera jamais de m’impressionner. Il semble qu’une relation très profonde existe entre l’ordre et le chaos, comme s’ils étaient totalement indissociables, comme si le chaos était généré à partir de l’ordre et que la réciproque était tout aussi pertinente.

Le diagramme de bifurcation se retrouve dans de nombreux domaines très éloignés les uns des autres comme la réception des ondes lumineuses sur notre rétine ou le comportement chaotique d’un robinet qui fuit. [voir la note 4]

L’illustre physicien théoricien Mitchell Feigenbaum a même découvert dans le diagramme de bifurcation une constante fondamentale de notre Univers : les nombres de Feigenbaum [Feigenbaum Constant chez Wolfram]

Cette intrication de l’ordre et du chaos est maintenant, grâce à la puissance de nos ordinateurs, accessible à des élèves de lycée, surtout depuis que la programmation a fait son entrée dans les programmes.

Au cours de cette narration de recherche, j’ai découvert de très nombreuses contrées mathématiques qui m’étaient inconnues. J’ai encore étendu les limites de mon ignorance et cela est bien l’objectif de ces recherches.