L’écriture itérative de l’algorithme d’Euclide présente l’avantage d’être courte et intéressante (parce que portant sur l’arithmétique). C’est donc un des exemples les plus simples illustrant la notion de boucle à sortie conditionnelle (à part peut-être ce jeu). Ceci dit le même algorithme illustre aussi la brièveté des codes basés sur la récursivité...
L’algorithme d’Euclide est basé sur le fait que le pgcd de a et b est aussi égal au pgcd de b et r, où r est le reste de la division euclidienne de a par b (en supposant que a>b) [1]. Pour l’implémenter, on a donc besoin de deux variables a et b, et chaque passage dans la boucle remplace a par b et b par r. Ces remplacements doivent être parfaitement simultanés sinon le calcul est entaché d’erreur (doit-on remplacer a par l’ancien b ou par le nouveau b ?).
Calcul parallèle
On en arrive donc à la recherche d’un algorithme parallèle : Si deux ordinateurs calculent chacun de son côté, l’un a, l’autre b, à eux deux ils iront deux fois plus vite en moyenne que si un seul d’entre eux faisait tout le travail à lui seul. À condition que ce soit possible !
L’affectation simultanée de deux variables est la spécialité du langage Lua, qui en plus possède un interpréteur en ligne, ça tombe bien ! Donc si on copie-colle le script suivant dans la fenêtre qui est à l’adresse ci-dessus, on peut calculer des pgcd par la méthode d’Euclide :
a=3600
b=3024
while(b>0) do
a,b = b,a % b
end
io.write("Le pgcd des deux nombres est ",a,"\n")
Comparer avec Python :
a=3600
b=3024
while (b>0):
a,b = b,a % b
print "Le pgcd est ", a
Et avec CoffeeScript :
pgcd = (a,b) ->
[a,b] = [b,a%b] until b is 0
a
alert pgcd 3600, 3024
En réalité il ne s’agit pas réellement de calcul parallèle mais de calcul matriciel : Lua considère que a,b est un vecteur dont les deux coordonnées sont mises à jour simultanément. Donc le même raccourci est implémentable avec SciLab ou Euler Math Toolbox puisque ces logiciels sont basés sur le calcul matriciel.
Un variante intéressante parce que graphique est ce CaRScript, qui calcule un pgcd sur une figure comprenant un point A (et on voit les étapes du calcul si on affiche les coordonnées de A) :
Move("A",3600,3024);
while(Y("A")>0){
Move("A",Y("A"),X("A")%Y("A"));
Pause(1000);
}
Le langage à la mode en calcul parallèle est Scratch, alors autant essayer avec Scratch : Puisqu’il y a deux variables à traiter, on peut les confier à deux lutins [2]. Le plus grand des deux nombres entiers (qui s’appelait a ci-dessus) est confié au lutin « Pégé » [3] et le plus petit au lutin « CéDé », représenté par un CD-Rom à droite de PéGé [4]. Le pgcd ne sera donc pas calculé par un acteur mais par PéGé et CéDé en travail collaboratif. Le remplacement simultané des deux variables « Nombre de PéGé » et « Nombre de CéDé » mène à un calcul faux (le pgcd est égal à 0, quelles que soient les valeurs de a et b). On doit donc créer une variable abritant temporairement le reste de la division euclidienne de a par b, le temps que a soit remplacé par b. La synchronisation des transformations de données se fait par des messages envoyés par la « scène » aux deux lutins. En calcul parallèle, on parle de sémaphore (informatique). Finalement, le calcul est partagé entre PéGé et CéDé, mais la scène joue le rôle de chef d’orchestre en synchronisant le travail de PéGé et de CéDé. Cette synchronisation se fera par envoi et réception de messages.
Pour commencer, il faut créer un projet Scratch, et ajouter à la scène les deux lutins PéGé et CéDé :
En cliquant sur un lutin, on voit apparaître à droite de l’écran, comment il est fait ; en particulier ses algorithmes, initialement vides.
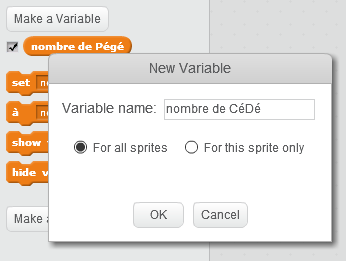
Lorsqu’on crée une variable comme « nombre de CéDé », on peut soit en faire une variable d’instance propre au lutin, soit une variable globale, accessible à tous les lutins (et à la scène, au besoin). Comme chaque lutin a besoin d’accéder à toutes les variables (soit pour les modifier, soit pour les afficher), on fait le second choix :
La scène va donc synchroniser les lutins :
- le démarrage du programme se fait lorsqu’on clique sur le drapeau vert, il consiste à initialiser les variables, puis
- entrer dans une boucle qui prend fin (ainsi que le programme) lorsque le reste euclidien est devenu nul, auquel cas le nombre de PéGé est devenu le pgcd cherché.
- Dans cette boucle, la scène envoie le message « divisez » puis attend que tout le monde soit synchronisé,
- et envoie le message « échangez »
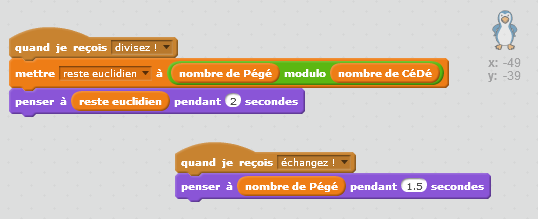
Le lutin PéGé a deux fonctions, selon le message qu’il reçoit :
- si c’est le message « divisez » il s’active et effectue la division puis affiche le résultat ;
- si c’est le message « échangez » c’est que c’est le tour de CéDé de travailler, alors PéGé fait une pause en attendant que CéDé ait fini, et pendant ce temps, se contente de rêver à son nombre :
Quant à CéDé, il n’effectue aucun travail si le message ne lui est pas destiné (« divisez » veut dire que c’est au tour de PéGé de travailler). Mais si le message qu’il reçoit est « échangez » il effectue l’échange en deux étapes :
- il met b dans a ;
- il met r dans b :
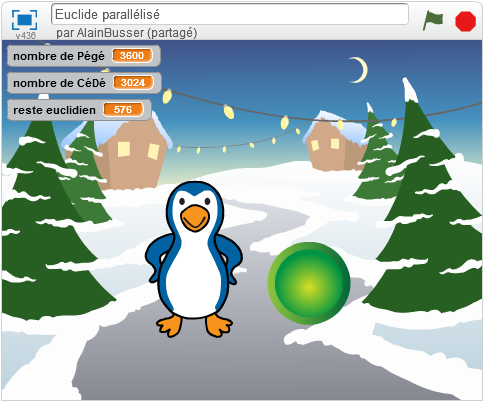
Pour calculer le pgcd de 3600 et 3024, on va donc sur le projet et on clique sur le drapeau vert. On voit alors ceci :
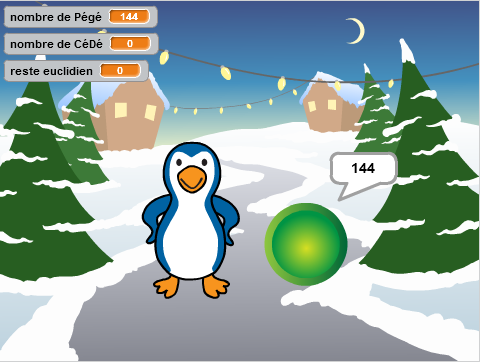
Puis, petit à petit, les variables sont affichées, et à la fin, CéDé affiche le PéGéCéDépgcd :
Si on veut calculer le pgcd d’autres nombres que 3600 et 3024, on peut modifier le projet, soit en mettant d’autres valeurs que 3600 et 3024, soit en ajoutant au projet des instructions d’entrée avec « demander » (« capteurs » en bleu clair).
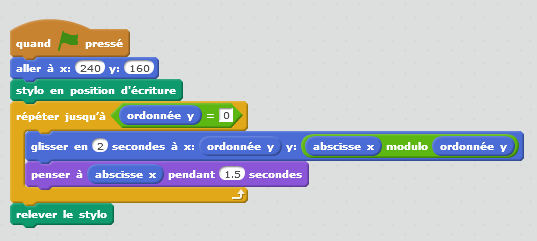
La scène peut être munie d’un ou plusieurs « arrière-plans », dont l’un représente un repère ; or l’algorithme d’Euclide peut être implémenté graphiquement en modifiant des coordonnées. On peut simuler un point mobile en prenant le lutin « ball » et en le redimensionnant. Au passage on coche les cases correspondant à abscisse (x) et à ordonnée (y) ce qui a pour effet d’afficher les coordonnées dans l’écran :
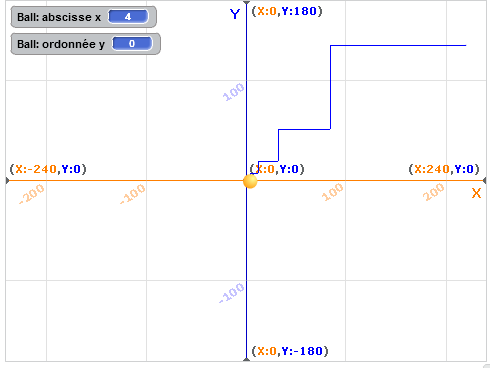
Ensuite, l’affectation simultanée des deux variables appelées a et b ci-dessus, se fait naturellement si a et b sont les coordonnées du lutin. Par exemple pour calculer le pgcd de 220 et 136 :
On peut même demander au lutin de laisser une trace de son passage :
Le projet est ici
On peut se diriger vers l’algorithme de tracé de segment de Bresenham avec la programmation graphique de l’algorithme d’Euclide avec soustractions, avec la même situation de départ mais cet algorithme pour le lutin :
Il laisse une trace dessinée de l’algorithme d’Euclide :
Le projet est ici
Cette réalisation où un seul processus fait séquentiellement le remplacement de a par b et b par le reste de la division euclidienne (avec une troisième variable pour les raisons évoquées ci-dessus) peut très bien être faite sous Scratch, mais je lui préfère personnellement JavaScript, en raison de la rapidité de la mise au point (y compris le débogage) avec les outils de développements existants : En bref, j’ai préféré choisir un outil plutôt qu’un langage.
Avec ce magnifique interpréteur en ligne qui est particulièrement adapté à des TP en Seconde (surtout si on s’en sert hors-ligne, ainsi on n’est pas tributaire d’un bon fonctionnement du réseau), le code produit en quelques minutes, débogage compris [5] est celui-ci :
var a=demander("Quel est le plus grand des deux nombres ?");
var b=demander("Quel est le plus petit des deux nombres ?");
while(b>0){
var t=a%b;
a=b;
b=t;
}
afficher("Le pgcd des deux nombres est ",a);
Autre outil particulièrement efficace, l’éditeur de CaRMetal donne quelque chose de plus « pro » avec des fenêtres d’alerte du plus bel effet ; le « CarScript » est légèrement différent du précédent :
a=Input("quel est le plus grand nombre ?");
b=Input("quel est le plus petit nombre ?");
while(b>0){
var t=a%b;
a=b;
b=t;
}
Prompt("Le pgcd des deux nombres est "+a);
On voit une différence au niveau de la création de l’affichage : Alors que l’éditeur en ligne affiche une liste de variables dont certaines sont des chaînes de caractères, CaRMetal affiche un seul texte, obtenu en concaténant un vrai texte (chaîne de caractères) et un nombre. Et l’affichage se fait dans une fenêtre ad hoc et pas directement dans l’outil de développement. Cependant les versions diffèrent peu...
On peut même profiter de l’intégration de JavaScript dans le format « web 2.0 » pour créer un fichier html comme celui qui est téléchargeable ci-dessous (« pgcd.html »). Cependant cela nécessite une petite connaissance du langage html et n’est guère réalisable en classe (ou alors en devoir maison ?) sauf si on fournit aux élèves un gabarit où seul le code JavaScript reste à écrire (celui qui a été reproduit dans le tableau du bas de la page « pgcd.html »).
Ceci dit, bien que nous quittions ainsi le programme de Seconde, la définition en tête de l’article « le pgcd de a et b est égal au pgcd de b et r » appelle une écriture récursive de l’algorithme. Surprenant, ça marche ! Bien que des langages soient spécialisés dans la récursivité (on pense à Maxima, pari->[http://pari.math.u-bordeaux.fr/down...] ou l’excellent xlogo mais il y en a plein d’autres), là encore une version JavaScript va être donnée, et là encore c’est plus à cause d’un outil qu’à cause du langage, puisqu’il s’agit d’un CarScript :
function gcd(a,b) {
// Implémentation de l'algorithme d'Euclide pour calculer un pgcd
if ((b % a) == 0){return (a);
} else {return (gcd(a,b-a));
}
}
for(i=1;i<4;i++){
// numérateurs
for(j=1;j<8;j++){
// dénominateurs
if(gcd(i,j) == 1){
// seulement si la fraction est irréductible
for(k=-4;k<4;k++){
// translations (pour éviter les trous)
a=Point("",k+i/j,1/j/j/2);
// centre du cercle
b=Point("",k+i/j,0);
// Point de contact avec l'axe des abscisses
c=Circle("",a,b);
SetRGBColor(c,32*i,2*i*j,16*j);
// La couleur du cercle dépend de sa taille
SetFilled(c,"true");
// On voit mieux si on le remplit
Hide(a);
Hide(b);
a=Point("",k-i/j,1/j/j/2);
b=Point("",k-i/j,0);
c=Circle("",a,b);
SetRGBColor(c,32*i,2*i*j,16*j);
SetFilled(c,"true");
Hide(a);
Hide(b);
}
}
}
}
Seules les 9 premières lignes concernent la fonction pgcd elle-même (fonction de deux variables soit dit en passant), le reste concerne une application de cette fonction pgcd, qui est utilisée dans la suite pour mettre des fractions sous forme irréductible : En effet, on montre que tous les cercles centrés sur les points de coordonnées $\left( \frac{p}{q} ;\frac{1}{2q^2}\right)$ et ayant pour rayon $\frac{1}{2q^2}$, où $\frac{p}{q}$ est irréductible, sont tangents ou disjoints. Un tel cercle s’appelle un cercle de Ford.
Le CarScript ci-dessus a servi à fabriquer la diapo numéro 5 de ce diaporama CaRMetal
Python n’a pas de lutins mais des threads : On va donc créer un diviseur et un échangeur qui effectuent respectivement la division et l’échange des données. Pour que chacun fasse son travail au moment où il est pertinent de le faire, on va les temporiser ; il faudra donc charger deux modules de Python :
- threading qui gère les threads
- time qui gère les pauses (« sleep »).
Le script doit donc commencer par ces imports :
from threading import *
import time
Le diviseur est défini comme un exemplaire de la classe Diviseur(). On doit commencer par définir celle-ci, en précisant qu’elle hérite de la classe Thread (le diviseur est donc bien un thread). Deux fonctions lui sont attribuées :
- __init__ qui détermine ce qui se passe au moment où on crée le diviseur ;
- run qui détermine ce qui se passe dans le thread une fois qu’on a démarré celui-ci avec start.
Lors de sa naissance, un diviseur se contente d’enregistrer les deux nombres a et b dont on veut calculer le pgcd, et d’afficher un message disant qu’il est prêt. Mais lorsqu’on le démarre, il fait 3 choses tant que la variable de l’échangeur n’est pas nulle :
- Il effectue la division euclidienne et stocke le reste dans la variable de l’échangeur ;
- Il affiche un message disant que la division est effectuée ;
- Il pique un petit somme (de 2 secondes) en attendant que l’échangeur ait fini son travail.
En Python cela donne
class Diviseur(Thread):
def __init__(self,a,b):
Thread.__init__(self)
self.a = a
self.b = b
print "Diviseur OK"
def run(self):
while echangeur.r > 0:
echangeur.r = self.a%self.b
print "Diviseur divise ", self.a, " par ", self.b
time.sleep(2)
Quant à l’échangeur, il n’a lui aussi que deux méthodes : __init__ qui affiche un faire-part de naissance et lui donne la variable r comme premier biberon, et run qui, tant que son contenu stomacal n’est pas vide, effectue ceci :
- faire une sieste d’une seconde en attendant que le diviseur ait fait son renvoi ;
- transférer la variable b (qui est au diviseur) dans a (qui est aussi au diviseur, ce n’est pas grave, il aime bien être palpé de l’intérieur par l’échangeur) ;
- transférer sa propre variable r dans b [6] (qui appartient toujours à l’échangeur) ;
- refaire une sieste en attendant que le diviseur ait divisé à nouveau :
class Echangeur(Thread):
def __init__(self,r):
Thread.__init__(self)
self.r = r
print "Echangeur OK"
def run(self):
while self.r != 0:
time.sleep(1)
diviseur.a = diviseur.b
diviseur.b = self.r
print "Echangeur echange ", diviseur.a, " et ", diviseur.b
time.sleep(1)
Ensuite, il suffit de créer un diviseur et un échangeur, puis de les démarrer, les joindre au script pour qu’il attende la fin des threads, et affiche le pgcd au bon moment :
echangeur=Echangeur(1)
diviseur = Diviseur(3600,3024)
diviseur.start()
echangeur.start()
diviseur.join()
echangeur.join()
print "Le pgcd est ", diviseur.a
En exécutant ce script Python, on voit apparaître au fur et à mesure l’état des différents threads actifs, et à la fin, le pgcd. Il est conseillé de modifier les durées pour voir l’effet produit sur le script (en particulier, ce qu’il faut faire pour avoir un pgcd faux). C’est un excellent exercice sur les droites graduées...










Commentaires