Les cartes à jouer
Voici une présentation de quelques infinitésimaux :
Le document source :
Et des cartes représentant des infiniment petits positifs et leurs opposés (qui sont donc négatifs) :
Avec le fichier source :
Dans son livre On Numbers and Games, Conway a défini une multiplication des surréels.
multiplication et infinitésimaux
Voici quelques exemples :
et le source en LaTeX :
La multiplication est compliquée à effectuer et on ne peut pas la représenter aisément sous forme d’opération sur les jeux. Toutefois, elle permet de modéliser les bases du calcul infinitésimal.
Principe de la dérivation
On prend pour exemple la fonction triple, qui, à un jeu J, associe le jeu obtenu en plaçant 3 copies de J l’une à côté de l’autre. Le triple d’un nombre s’obtient, en fait, en multipliant ce nombre par
Le triple d’un nombre est un nombre, mais le triple de
est
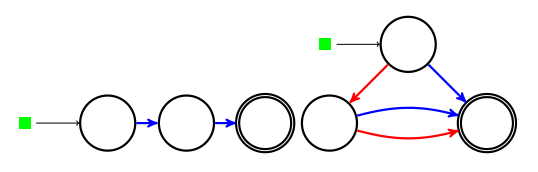
qui n’est pas un nombre : c’est la somme d’un nombre positif et d’un infinitésimal. Ce jeu est donc largement positif et peu intéressant à jouer. On peut cependant neutraliser le nombre en additionnant son opposé :
On a alors un jeu plus intéressant à jouer, parce qu’il est infinitésimal :
L’idée de l’analyse de Leibniz est d’estimer cet infinitésimal (appelé différentielle), et en particulier combien de fois y entre l’infinitésimal qu’on avait ajouté à 2 au départ.
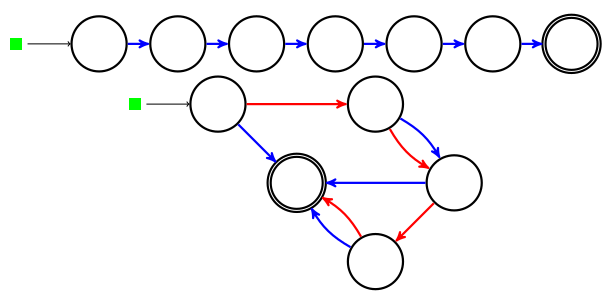
Or il se trouve qu’en effectuant (difficilement) le produit du nombre
par l’infinitésimal
on obtient précisément
qui est le jeu infinitésimal obtenu ci-dessus. En général, l’infinitésimal
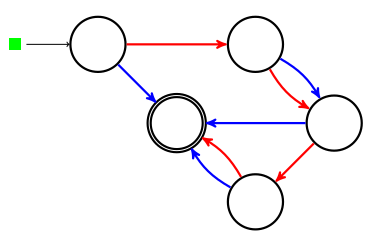
est à multiplier par autre chose qu’un nombre pour avoir exactement la différentielle, mais par la somme d’un nombre et d’un infinitésimal, et c’est ce dernier nombre qui est la dérivée. Pour la fonction triple, on apprend donc que sa dérivée en
est le nombre le plus proche de
soit
lui-même, puisque le résidu infinitésimal est, dans ce cas, égal à 0.
En fait, dans cet exemple précis (la fonction triple), la dérivée en n’importe quel nombre est le même nombre 3. D’où le nom de triple donné à la fonction.
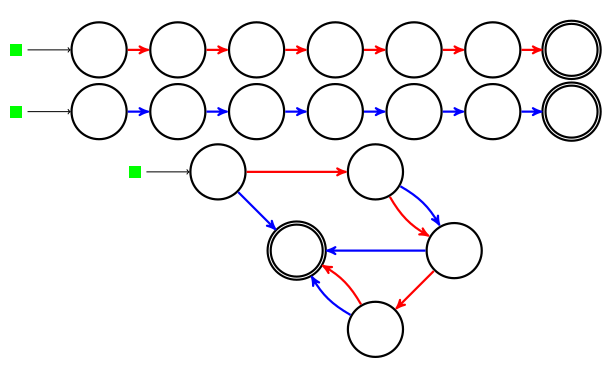
Pour les polynômes, il faut souvent développer et réduire. Voici des exemples de calculs de nombres dérivés des fonctions carré et cube :
| fonction | carré | cube |
| exemples |
|
|
| source |
|
|
Infinitésimaux dans des vrais jeux
Des infinitésimaux (en particulier up) ont été découverts
- dans konane
- dans alquerkonane
mais Noam Elkies en a trouvé aussi dans le jeu d’échecs. Voici des exemples :
avec le source :
Commentaires