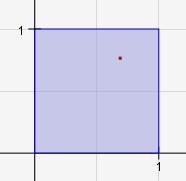
On voudrait que le point rouge parcoure le carré unité (en bleu) lorsqu’on chatouille le singe :

Ce point s’appelle P2, et P1 est un point mobile caché mais placé dans la fenêtre. Les coordonnées de P2 sont données par

Par cette transformation, la fenêtre a pour image le carré unité, et donc P2 bouge dans le carré.

Pour un autre quadrilatère Q, on peut adapter ces formules mais aussi chercher une affinité qui transforme le carré unité en Q (elle peut être définie par une macro).

On va modifier l’exemple de l’onglet précédent, pour avoir un rectangle. L’abscisse doit toujours être comprise entre 0 et 1 mais l’ordonnée doit aller de 0 à $2 \pi$ (on s’en servira tantôt comme argument).

(L’ordonnée est un peu longue et on ne voit pas le début de l’expression ; c’est juste le produit de celle de l’onglet précédent par 2*pi, soit

(y(P1)+windowh/2-windowcy)/windowh*2*pi

Maintenant ce point P2 va être caché, et ses coordonnées utilisées pour calculer celles d’un troisième point, nommé P5 (parce que P3 et P4 ont servi à construire le cercle), et dont les coordonnées sont

Alors, tant qu’on agace le rhésus (en cliquant dessus), P5 semble parcourir l’intérieur du disque unité :

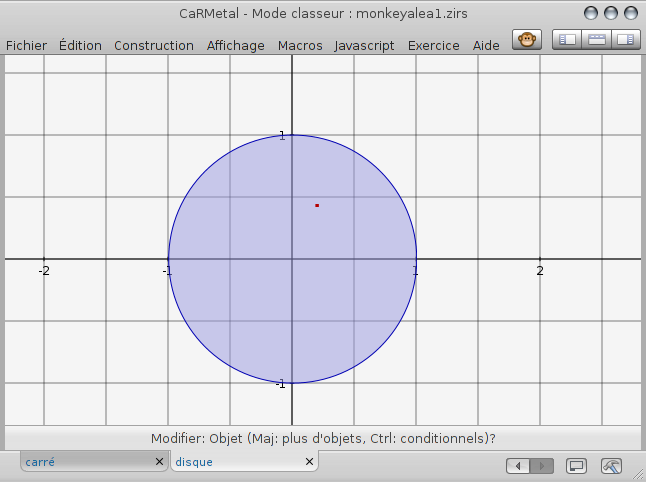
Cependant, le mouvement dans le cercle ne semble pas être uniforme.

Une homothétie permet alors de remplacer ce point simiesquement lié au disque unité, en un point qui bouge dans un autre disque ; et une affinité permet d’obtenir un point qui reste à l’intérieur d’une ellipse.

On pourrait de même transformer le carré unité en un triangle par une affinité, mais le sommet qui est image commune de 2 sommets du carré serait visité plus souvent que le reste du carré. Il vaut alors mieux choisir une transformation affine par morceaux, ce qui est assez facile lorsque le triangle occupe la moitié inférieure du carré unité :

Là encore, un point P2 a été créé comme dans l’onglet « carré » (et caché), et ses coordonnées utilisées pour calculer celles de P5 :

Alors on a beau énerver le singe aussi longtemps qu’on veut, le point P5 (en rouge ci-dessus) persiste à rester enfermé dans le triangle.

Pour avoir un effet analogue avec d’autres triangles, il suffit d’appliquer au point P5 ci-dessus, l’unique affinité qui transforme le triangle rectangle isocèle, en le triangle voulu. L’élaboration de cette affinité peut être l’objet d’un exercice intéressant de construction de macro...

Le procédé est généralisable à des polygones ayant plus de 4 côtés, en tronquant par exemple le carré par d’autres droites que sa diagonale.