Jeux de Nim
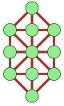
L’article wikipedia sur les jeux de Nim montre un exemple de graphe du jeu, avec des couleurs différentes pour les positions gagnantes et les positions perdantes. La légende de ce graphe dit que « Le but du jeu est de déplacer un jeton d’un sommet à l’autre selon les arêtes indiquées ». Le principe est alors repris en dessinant un graphe et en laissant les joueurs glisser un pion [1] sur le graphe.
Note : Pour trouver la stratégie gagnante, il faut colorier ou numéroter les cases, ce qui n’a pas été fait ici ; mais la numérotation implicite est faite en remontant depuis la case d’arrivée, laquelle est numérotée 0.
Voilà comment on peut avancer de deux cases, en faisant glisser le pion le long d’une arête rouge :

ou de trois cases, en faisant glisser le pion le long d’une arête bleue :

La règle du jeu :
Et si on veut jouer en ligne, voici le jeu :
On constate que si on est à 1, 2 ou 3 cases de l’arrivée, on gagne (des flèches permettant de faire le parcours). Le coup joué ci-dessous est donc perdant puisqu’il finit à 3 (qui est gagnant pour l’adversaire, en jouant le bleu) :
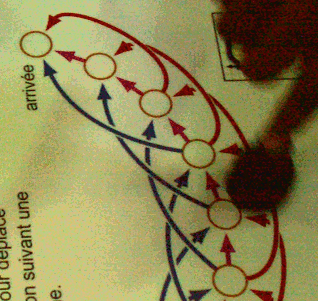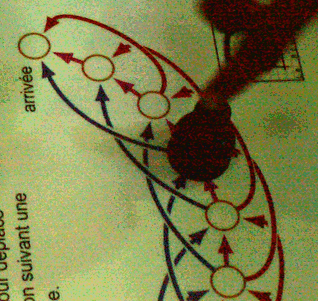
Pourtant il était possible de gagner, en ne jouant pas le rouge (2 cases) mais le mauve (1 case) ; dans ce cas l’adversaire ne pouvait pas gagner mais ne pouvait pas faire autrement que mettre le pion dans une position gagnante.
D’ailleurs la mine réjouie de l’adversaire en dit long :

Rapidement les enfants comprennent que cette case située à 4 unités de l’arrivée est gagnante s’ils y mènent le pion. Au point que la partie s’arrête là et plus à l’arrivée. Il est plus rare que l’on comprenne que du coup la case située à 8 unités de l’arrivée est aussi gagnante puisqu’en y menant le pion, on peut au coup suivant atteindre la case gagnante située à 4 unités :

Personne ou presque n’est allé jusqu’à la constatation que la case 12 aussi est gagnante, pour les raisons exposées ci-dessus

Et depuis la case 14, on peut donc gagner en jouant le rouge pour aller vers la case 12 :

Ôtez un carré
Cette variante vient des jeux mathématiques du Monde (4 mars 1997) :
| Deux joueurs disposent d’un tas d’alumettes. Chacun, à son tour de rôle, ôte un certain nombre, non nul, d’allumettes du tas, ce nombre ôté devant impérativement être un carré : 1, 4, 9, 16, 25 ... Le joueur enlevant la dernière allumette a gagné. |
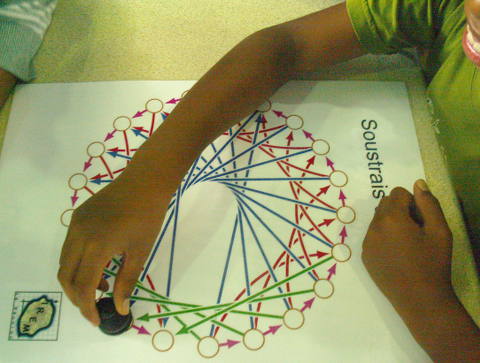
Dans le graphe du jeu,
- les arêtes mauves représentent la soustraction de 1 (qui est un carré) ;
- les arêtes rouges représentent la soustraction de 4 ;
- les arêtes bleues représentent la soustraction de 9 ;
- et les arêtes vertes représentent la soustraction de 16.
Ici, le joueur joue mauve (-1) et gagne puisque 1 est un carré :
Si on est sur la case 2, on perd puisque le seul coup qu’on puisse jouer est 1 (mauve) ce qui mène à la position gagnante (pour l’adversaire) vue ci-dessus. Dans la vidéo ci-dessous, l’un des joueurs joue le rouge (-4) pour amener le pion à la case 2 et effectivement, l’autre joueur perd (et s’en vite compte d’ailleurs) :
Voici une partie complète basée sur cette fin (le perdant de tout-à-l’heure prend sa revanche) :
- La première joue -1 ce qui fait passer de la case 20 à la case 19 ;
- le second joue -4 (rouge) ce qui fait passer à la case 15 ;
- la première joue -9 ce qui fait passer à la case 6, et on est dans la situation symétrique de celle de la partie précédente :
- Le second joueur joue -4 ce qui l’amène à la case 2 ;
- et les joueurs réalisent alors que le second a gagné, et s’arrêtent de jouer.
Ensuite, pour les raisons vues ci-dessus, la case 3 est gagnante puisque si on y est, en jouant 1 on arrive à la case 2 ce qui, on l’a vu, fait perdre l’adversaire. Ici, en jouant rouge, on arrive à cette case 3 qui fait gagner l’adversaire :
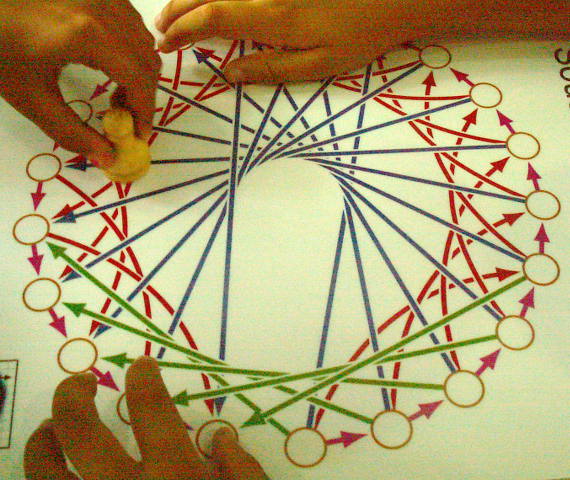
Par contre, comme 4 est un carré, la case 4 est perdante (en suivant l’arête rouge) :
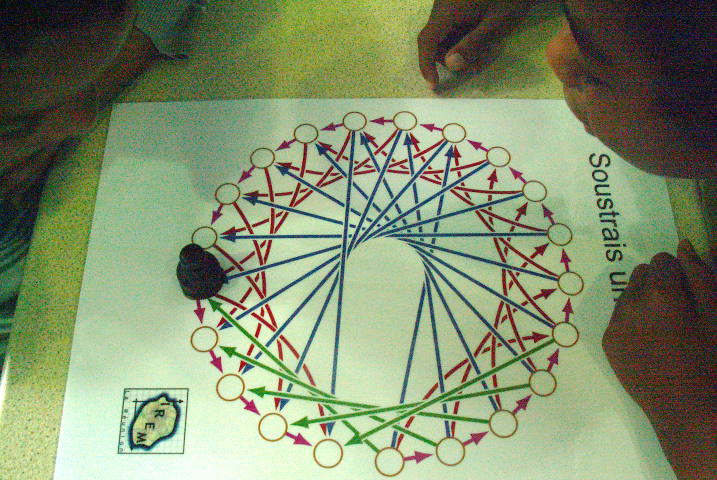
Comme 20=16+4, si le premier joueur joue la flèche verte, il perd puisque cela le mène à la case 4 qui, on l’a vu, est perdante. Certaines parties de débutants sont donc très courtes ! Si le premier joueur joue rouge (-4), c’est pareil, le second gagne en jouant vert (-16).
Jeux de poursuite

Le jeu militaire est, d’après Edourd Lucas, un jeu à la mode à la fin du XIXe siècle, inventé par un militaire (d’où son nom) retraité, et basé sur un vocabulaire issu de l’armée. En fait il ne s’agit que d’une variante du jeu du lièvre et du chien, un jeu médiéval qui lui-même est une simplification des jeux de tigre qu’on trouve dans toute l’Asie, mais aussi une variante d’un jeu dit « de l’ours » que l’on jouait dans la Rome antique. Les jeux asiatiques, dont les plateaux sont de remarquables œuvres d’art, permettent de prendre des pions comme aux dames, ce qui les rapprocherait plus du fanorona. Par contre, le jeu de go est basé sur la même idée d’encercler un pion.
En 1887, dans la revue La Nature, Edouard Lucas analyse le jeu militaire, qu’il décrit comme inventé peu avant par un militaire retraité appelé Louis Dyen. Cette analyse du jeu est intéressante parce que Lucas dénombre les positions possibles du jeu et fait un arbre du jeu (« tableau général des parties » à la dernière page). Cet article vaut la peine qu’on le lise ne serait-ce que pour profiter du style ironique de Lucas. Le voici en pdf :
La règle du jeu est plutôt simple :
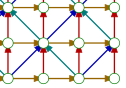
| Pour jouer, on déplace un de ses pions vers une place verte disponible (qui ne soit pas déjà occupée), sans quitter le chemin (en marron). Le joueur qui a les chiens choisit à chaque tour, lequel des chiens ils veut bouger, mais les chiens n’ont pas le droit de reculer. Le but du jeu est, pour les chiens, de coincer le tang, et pour le tang, d’échapper aux chiens en passant derrière eux. |
Comme le joueur qui joue en premier n’a qu’un choix possible, on peut faire commencer les chiens (« tours ») et prendre comme position de départ, celle où le pion a déjà avancé. Cela permet de rapidement s’exercer à ce jeu en ligne :
L’affirmation « les blancs gagnent toujours en une douzaine de coups, au maximum » signifie qu’il existe une stratégie gagnante pour les chiens (« blancs »). Pour autant, celle-ci n’est pas facile à trouver ni retenir et à la fête de la science, les parties gagnées et perdues étaient approximativement équiréparties.
Pour éviter de perturber les enfants avec des histoires de stratégie militaire, on a fait un peu « couleur locale » avec des chiens cherchant à bloquer dans son terrier, un tenrec ecaudatus (« tang », en créole ; en effet le chien n’attaque pas le tang mais ne fait que l’acculer dans son terrier). Le succès de ce jeu a été tel qu’il a fallu improviser un second jeu de pions :

Le but du jeu, pour les chiens, est de créer un mur bloquant le tang :

Pour le tang, évidemment, le but est d’échapper à ce mur en se glissant dans une faille de celui-ci. Mais la perception des diagonales n’est pas toujours parfaite ce qui amène certains enfants à « tricher » (le second coup ci-dessous est interdit puisqu’il n’y a pas de chemin en diagonale) :
Une stratégie qui apparaît vite chez les maîtres-chiens consiste à construire puis propager un mur, dès le début de la partie. Voici un début de partie typique :

Et voici une partie presque complète, qui se solde sans grosse surprise par une défaite du tang (à droite) :
Dans la situation suivante, où les chiens jouent, ils peuvent gagner mais à condition de bien s’y prendre :

Voici une partie où le tang gagne (erreur des chiens) :
Une autre où le tang peut s’échapper par le haut (puis la gauche, les chiens n’ayant pas le droit d’aller à gauche) :
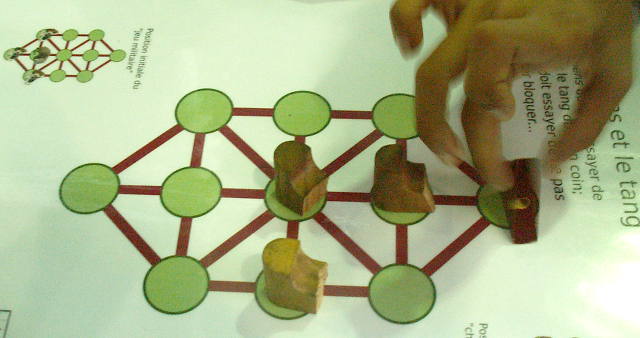
Plusieurs enfants ont voulu essayer la version médiévale où le tang part de l’autre bout. Là, si ce sont les chiens qui commencent, ils gagnent plus difficilement (en essayant un coup interdit à la fin) :
Si c’est le tang qui commence ça donne ça :

Qui va gagner ?
Une technique classique quand on joue c’est de regarder non le plateau de jeu, mais le visage de l’adversaire, dans l’espoir d’y lire ses intentions :

Pour finir, quelques exercices (on peut se servir de la version en ligne ci-dessus comme support de raisonnement) :
- Chaque joueur a joué trois coups depuis de début le partie ; lesquels ? Qui gagne ?

- Le tang joue et gagne. Est-il possible que la position initiale des chiens ait été à gauche de la photo ?

- Quels sont les coups qui ont été joués pour aboutir à cette position ?

Pour aller plus loin, voici un autre jeu de poursuite, sur un graphe plus équilibré ; on peut y jouer en ligne :
Bibliogaphie/Webographie
- sur le jeu de Nim et son histoire
- Edouard Lucas, « récréations mathématiques », disponible sur Gallica ou ici. Le jeu militaire est décrit dans le tome 3, mais bien d’autres jeux combinatoires sont intéressants, notamment celui du « fer à cheval », en apparence très simple.
- le jeu de la soustraction programmé en Scratch (langage) par Benjamin Clerc
- la théorie du jeu de Nim et des variantes intéressantes
- les jeux de Nim sur échiquier












Commentaires