Objectifs du TP

Il s’agissait d’introduire

• La géométrie repérée, l’un des exercices nécessitant la lecture de coordonnées de points sur la figure finie.
• La notion de boucle à nombre prédéterminé d’exécutions.
• Une révision discrète sur les fonctions affines.

Tout ça fait rétrospectivement un peu beaucoup...

Pour commencer, une explication au tableau :

On souhaite tracer le cercle dont le centre a pour coordonnées (0,1 ;0,01) passant par l’origine ; l’ordonnée a été calculée auparavant comme étant le carré de l’abscisse.

Mais on voudrait aussi avoir sur la même figure, le cercle dont le centre a pour coordonnées (0,2 ;0,04) et passant lui aussi par l’origine,

et aussi celui de centre (0,3 ;0,09) passant par l’origine,

etc.

Peut-on faire ceci avec un CarScript ?

En réponse aux soupirs découragés des élèves (« ce serait bien que JavaScript fasse tout ça automatiquement ») les termes de boucle et d’indice ont été introduits, puis le sujet du TP distribué. Le voici [1] :

Première boucle

Le premier exercice, fait correctement, donne ceci :

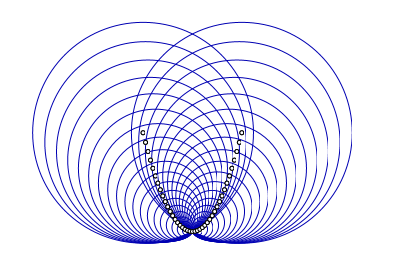
Mais si un élève oublie un « = » dans la deuxième partie de la déclaration de la boucle, ce qui fait qu’au lieu d’aller jusqu’à 20, i va jusqu’à 19, le résultat, bien que peu visible sur le script lui-même, se voit immédiatement sur le résultat :

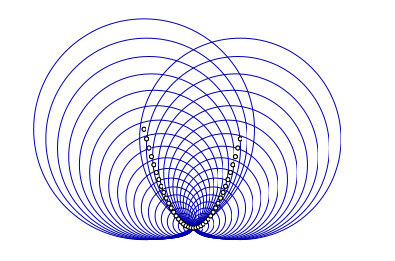
La majorité des élèves semble préférer tout taper au clavier que cliquer puis modifier ce qu’ils obtiennent. C’est sans doute dû au fait qu’en l’occurence ils avaient un texte à recopier.

Par contre, très peu d’élèves pensent à cliquer sur le bouton « undo » pour vider la figure avant de réessayer. Il y en a même eu qui effaçaient les points un à un avec l’outil « poubelle » de CaRMetal ! Le fait que lorsqu’on essaye plusieurs fois le script, les objets deviennent de plus en plus nombreux et chargent la mémoire de l’ordinateur, est plutôt bénéfique puisqu’il « punit » ceux qui préfèrent cliquer avant de réfléchir...

Bien qu’ils aient entendu parler de l’instruction « Pause » pour voir ce que donne le script, aucun élève ne l’a utilisée. D’ailleurs peu d’entre eux ont pensé à réduire la fenêtre JavaScript pour voir en « live » l’exécution du script.

Par contre le relevé des coordonnées du point le plus à gauche de la figure a été en général correct, puisque souvent les élèves savaient ce qu’ils étaient censés trouver.

Nuage de points

Bien qu’on sorte ici du cadre des CarScripts, 9 élèves ont trouvé le bon intervalle $[-4 ;4[$ alors que 8 ont donné à la place $[0 ;100[$ et même 8 d’entre eux ont donné $[0 ;+\infty[$ sans doute à cause de la borne supérieure non comprise.

9 élèves ont pensé au lien avec une fonction affine, dont 3 ont su donner la fonction $x \mapsto \frac{x}{2}+1$. Outre les classiques disciples de Jacques II de Chabannes de La Palice (« ils sont alignés car ils sont sur une même droite »), deux élèves ont estimé que « quand il y a un ++, les points sont forcément alignés ». Les mécanismes de création d’erreur sont donc très similaires en programmation et en géométrie.

Tableau de fils

Le tableau de fils était donné sur l’énoncé, avec la tâche de le reproduire. Bien que les enveloppes soient courbes [2], tous les élèves ont vu qu’il s’agissait de tracer une famille de segments, sauf un, qui après coup a fait chez lui ceci :

a=Point(-10,0);{
	b=Point(0,-10);
	c=Point(0,10);
	d=Point(10,0);
	f=Point(-10,10);SetHide(f,true);
	i=Point(-10,-10);SetHide(i,true);
	l=Point(10,10);SetHide(l,true);
	m=Point(10,-10);SetHide(m,true);
	v=Circle(f,a)
	n=Circle(i,b);
	u=Circle(m,d);
	r=Circle(l,c);
	s=Segment(c,b);
	s=Segment(a,d);
	o=Point(0,0);
	for(g=-10,0;g<=0,0;g=g+1);
	x=g/10;
	y=Math.pow(x,2);
   u=Point(x,y);
//à multiplier et à modifier pour obtenir tout les points.
	}

La boucle a visiblement été inspirée de l’exercice 1, et on voit surtout la réticence à faire exécuter une boucle (il aurait par exemple été possible de regrouper les 4 cercles dans une boucle). On voit également spontanément apparaître une utilisation des commentaires qui est apparemment classique chez les programmeurs, pour rappeler en quoi le programme (jugé, à juste titre, inachevé par l’élève) doit être amélioré. Le script en question donne la figure suivante :

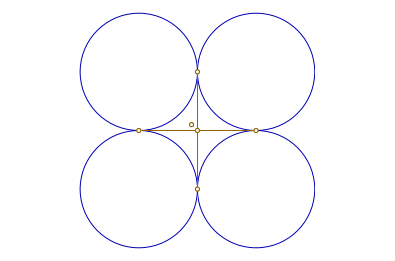
La difficulté de cet exercice est double :

1. Pour tracer les segments, il faut lire les coordonnées de leurs extrémités, à partir de la donnée des coordonnées des points les plus extrêmes de la figure.
2. Ensuite il faut trouver comment construire la (les) boucle(s).

Déjà, la première étape fut jugée difficile par les élèves, qui ont vite perçu que les coordonnées des points étaient entières et que l’une d’entre elles était nulle, mais beaucoup d’entre eux confondent l’abscisse et l’ordonnée ou se trompent dans le sens des axes...

Et beaucoup d’entre eux ont dit n’avoir pas bien saisi ce qu’est une boucle.

Une boucle, c’est quelque chose de difficile.

Le script ci-dessous

o=Point(0,0);SetHide(o,true);
N=20;
for (i=0; i<N; i++){
	t=2*Math.PI*i/N;
	a=Point(Math.cos(t),Math.sin(t));SetHide(a,true);
	b=Point(Math.SQRT2*Math.cos(t+Math.PI/4),Math.SQRT2*Math.sin(t+Math.PI/4));SetHide(b,true);
	c=Point(-Math.sin(t),Math.cos(t));SetHide(c,true);
	t=Polygon("",o+","+a+","+b+","+c);
}

produit le dessin suivant :

En dehors de l’utilisation d’angles en radians, il est clair qu’on ne peut attendre d’un élève de Seconde la production de ce genre de figure, du moins pas sans une préparation de plusieurs semaines. Or la même figure avait été produite sans problème par tous les élèves d’une classe de cinquième avec le script xlogo suivant :

pour carré
repete 4 [av 50 tg 90]
fin

repete 20 [carré tg 18]

Comment ce qui a été facile en cinquième peut être difficile en Seconde ?

• Il se peut que certaines notions d’algorithmique soient plus aisément perceptibles par des enfants que par des adolescents (?) ;
• Dans le cas de LOGO, la boucle ne comporte pas d’indice et il suffit de se dire qu’on effectue la tâche 20 fois. Dans le programme de Seconde, on a besoin (par exemple pour représenter graphiquement une fonction) que la tâche répétée dépende de variables : les indices de la boucle.
• La syntaxe des boucles n’est pas extrèmement simple en JavaScript : Une boucle est décrite par trois choses :
  • une valeur de départ pour l’indice,
  • une valeur d’arrivée,
  • et le pas (plus bien sûr le nom de l’indice)

alors qu’en JavaScript, comme dans les langages objet, la valeur de départ est donnée par une affectation comme il se doit, et le pas est remplacé par une affectation dynamique, ce qui est plutôt mieux, mais la valeur de fin est remplacée par une condition pour rester dans la boucle, ce qui est loin d’être simple. Cette notation, inventée par Dennis Ritchie et très populaire dans les langages objet, est visiblement difficile d’accès pour les élèves de Seconde.

Par contre la similitude entre JavaScript et les langages objet m’a servi à utiliser CaRMetal comme tremplin vers ces langages : Asymptote, Java, c++ et xcas me semblent plus faciles à déchiffrer qu’avant ces séances CarMetal...

À titre de comparaison la notation des calculatrices graphiques, inspirée de BASIC, est plus simple à saisir : « for(i,-20,20,1) ». Celle de Algobox « pour i allant de -20 à 20 » encore plus, celle de Scratch est la même que celle de LOGO, donc sans faire référence à l’indice.

Le processus d’apprentissage de la notion d’itération est analysé en détail dans cet article qui est un « must » (voir en particulier l’onglet 3).

Une explication possible à cette difficulté de percevoir que l’indice va de -20 à 20, est le fait que les élèves qui ont le plus de difficulté perçoivent mal que, en ajoutant 1 à -20, on obtient -19... Ainsi l’exercice sur le nuage de points faisait appel à des nombres pseudo-aléatoires et n’utilisait pas l’indice. Beaucoup d’élèves ont compris qu’on avait construit 100 points placés aléatoirement et tenté de s’en inspirer pour faire un tableau de fils pseudo-aléatoire...

Ainsi, un exemple typique est celui-ci

o=Point(-10,0);SetHide(o,true);
p=Point(10,0);SetHide(p,true);
s=Segment(o,p)
for (i=0; i<10; i++){
q=Point(0,-10);SetHide(q,true);
r=Point(0,10);SetHide(r,true);
s=Segment(q,r)
}

où on se contente de créer 11 fois le même segment (dont 10 dans la boucle), faute d’avoir songé à utiliser l’indice dans le corps de la boucle...

for(i=20;i>=0;i--)

function premier(n){//    fonction booléenne
var diviseur_potentiel=2;
var prime=true;//    nombre premier a priori
while(diviseur_potentiel*diviseur_potentiel<=n){
if(n % diviseur_potentiel == 0) prime=false;// nombre composé a posteriori
diviseur_potentiel++;
}//fin boucle while
return(prime);
}//fin définition fonction

function premier(n){//    fonction booléenne
	prime=true;
for(diviseur_potentiel=2;diviseur_potentiel*diviseur_potentiel<=n;diviseur_potentiel++){
	if(n % diviseur_potentiel == 0) prime=false;
}//fin boucle for
	return(prime);
}//fin définition fonction

for(p=1;p<Infinity;p=p*10)Println(p);

Voici un exemple de ce qui a été produit par un groupe de deux élèves [3] :

for(i=0;i<=10;i++){
a=Point(i,0);
b=Point(0,i);
s=Segment(a,b)
	}

La figure obtenue est la suivante :

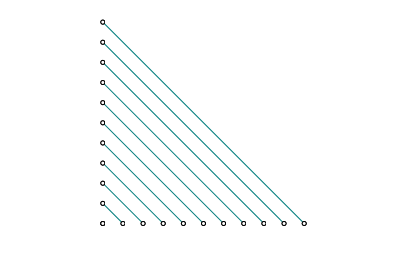
avec la nette impression qu’on n’est pas loin de la solution.

Lire des coordonnées, c’est plutôt facile.

Un CarScript qui peut aider pour le corrigé du TP :

for(n=-10;n<=10;n=n+1){
	a=Point(n,0);
	SetShowValue(a,true);
	b=Point(0,n);
	SetShowValue(b,true);
	}

Il produit la figure que trop peu d’élèves ont essayé de faire au brouillon sur papier :

La différence essentielle entre LOGO et CaRMetal, c’est que ce dernier travaille directement en géométrie repérée, donc dans un repère fixe (que certains élèves ont d’ailleurs choisi d’afficher) alors que LOGO travaille dans un repère de Frénet ce qui signifie concrètement que pour raisonner en LOGO on se livre parfois à des contorsions devant l’écran. Comme le montre cet article, il en est de même en Scratch [4]. Or raisonner en coordonnées locales est a priori plus difficile que raisonner dans un repère fixe. Pourtant, le langage LOGO (et de plus en plus, Scratch) a été sujet à des expériences réussies dans des petites classes. Mystère...

En tout cas, comme dans l’article suscité, l’intérêt de sortir une feuille de papier pour repérer des points d’après leurs coordonnées est perceptible, plusieurs élèves l’ayant fait, sans succès faute de temps.

Voici un exemple de script créé par une élève qui avait fait le dessin sur la feuille :

/*Tableau de fils
PRUGNIÈRES.marie
27/9/2009 */


var j=10;
for(i=0;i<=10;i++){
	a=Point(i,0);
	b=Point(-i,0);
	c=Point(0,j);
	d=Point(0,-j);
	e=Point(-i,-j);

	//x>0;y>0;
	s=Segment(a,c);

	//x>0;y<0
	s=Segment(a,d);

	//x<0;y>0
	s=Segment(b,c);

	//x<0;y<0;
	s=Segment(b,d);

	SetHide(a,true);
	SetHide(b,true);
	SetHide(c,true);
	SetHide(d,true);
	SetHide(e,true);

	j=j-1;

}

(on remarque la présence d’un point « e » superflu, c’est un bon moyen de repérer ceux qui copient).

Et voici un exemple fait par un élève dans les jours qui ont suivi le TP :

for(n=0;n<=10;n++){
	a=Point(10-n,0);SetHide(a,true);
	b=Point(0,n);SetHide(b,true);
	s=Segment(a,b);
	c=Point(0,-n);SetHide(c,true);
	t=Segment(a,c);
	d=Point(-10+n,0);SetHide(d,true);
	u=Segment(c,d);
	v=Segment(d,b);
}

Ces deux derniers exemples donnent bien le tableau de fils, et sont plus complexes que ce qui était attendu (j’imaginais 4 boucles, une pour chaque arc de parabole).

Conclusions

Il résulte de cette expérience pas très heureuse que les boucles devraient être vues

• Plus tard dans l’année, non pour une question de maturité mais parce que les généralités doivent être bien maîtrisées par les élèves pour se concentrer sur la difficulté que représente la gestion de l’indice et ce qui en dépend : Une boucle c’est une affectation successive de la variable indice, et ne peut être appréhendée que par un élève qui sait bien ce que signifie le mot « affectation ».
• Dans des exemples presque vides où on se contente d’afficher les valeurs successives de l’indice, éventuellement avec des « Pause ».

for(indice=-5;indice<=7;indice++){
	Println("Maintenant indice vaut "+indice);
}

for(indice=15;indice>=3;indice--){
	Println("Maintenant indice vaut "+indice);
}

for(indice=0;indice<1;indice=indice+0.1){
	Println("Maintenant indice vaut "+indice);
}

Dans cette optique, j’aurais du utiliser l’instruction « Move » de CaRMetal, qui, combinée avec « Pause » et l’affichage des coordonnées du point, aurait permis d’insister à la fois sur l’aspect dynamique des boucles, et sur les coordonnées...

• Après des révisions sur l’addition des relatifs, puisque ce semble être le principal mécanisme de blocage chez les élèves les plus en difficulté...

L’impression qui se dégage de tout ça est que, parce qu’une boucle est une répétition d’affectations dynamiques d’une variable, tout élève qui a mal perçu l’aspect dynamique des modifications de variables, aura aussi du mal à exploiter des boucles. C’est à ce stade que l’hétérogénéité des élèves commence à se manifester, et l’évaluation de l’algorithmique au futur bac STG promet des sueurs froides...

Postface

Le contôle qui a suivi ce TP est téléchargeable ci-dessous (au format pdf). Seul l’exercice 2 portait sur JavaScript. Il est en deux parties, une facile (parce que déjà faite en classe), portant sur l’écriture en ligne, l’autre plus difficile car portant sur les boucles.

Or l’exercice facile a été peu réussi, plusieurs élèves ayant répondu 24 (il y a même eu un -4, ?) et peu d’entre eux ayant pu expliquer pourquoi b=3,3 avec le calcul de fraction qui était demandé.

Quant à la deuxième partie, elle a surtout révélé que la notion de boucle n’est toujours pas saisie. Voici une ébauche de corrigé :

Or pas un seul élève n’a trouvé x=14 à la fin. Les causes d’erreurs sont multiples :

• La réponse i=3 a déjà été plus rare que la réponse i=2. Au moins un élève a vu dans "i<=3" un $i<3$ au lieu de $i\leqslant 3$. Au moins un autre a cru au contraire que le plus grand entier inférieur ou égal à 3 est 2, et ignorait donc que $3 \leqslant 3$...
• Souvent i=2 était associé à x=8 mais pas toujours.
• L’instruction x=x+2*i a été parfois vue en-dehors de la boucle ; avec i=3 ça donne x=2+2*3=2+6=8 (énoncé mal conçu : Deux causes différentes d’erreur donnant la même erreur).
• Visiblement le fait que la valeur de x qui est utilisée dans le calcul de la boucle change tout le temps est une difficulté supplémentaire : Celle de trop ?
• Beaucoup d’élèves n’ont même pas compris que quand on arrive à la fin de la boucle on recommence au début, bref le concept même de boucle n’est pas perçu. L’un d’eux a tout de même développé une vision statique de la boucle, comme si i était égal simultanément à 1, 2 et 3. Ce qui ne l’a pas aidé à trouver la valeur de x mais cet élève semble être fait pour programmer en SciLab...

Bref l’utilisation de boucle pour calculer la somme des premiers entiers est loin d’être aussi naturelle que prévue...

L’article qui va sans nul doute devenir un « best downloader »