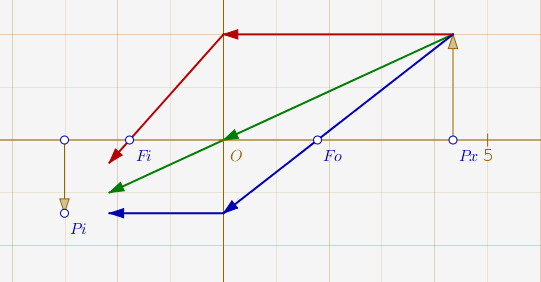
Le principe de la construction est le suivant : pour une lentille convergente (comme les loupes et objectifs des appareils photo), tous les rayons issus d’un point (l’objet) passent par un autre point (l’image). On peut donc construire l’image comme intersection de trois rayons remarquables :
- celui qui est parallèle à l’axe (il passe ensuite par le foyer image ; en rouge dans l’animation ci-dessous) ;
- celui qui passe par le foyer objet (il devient ensuite parallèle à l’axe ; en bleu dans l’animation ci-dessous) ;
- celui qui passe par le centre de la lentille (il n’est pas dévié ; en vert ci-dessous).
Comme le fait qu’un rayon puisse ne pas être dévié me paraissait peu intuitif, j’ai choisi les deux premiers rayons, qui se construisent avec des droites par deux points et des parallèles. Or le fait qu’il faut pour construire la parallèle à l’axe des abscisses par un point, avoir construit préalablement le point, n’est pas encore évident pour tous les élèves de Seconde [1]. Le manque de pratique de la géométrie dynamique se voit jusqu’à la maladresse de certains élèves qui n’arrivent pas à cliquer au bon endroit lorsqu’il faut sélectionner un point pour construire une droite passant par ce point : parfois l’élève clique à côté et crée un nouveau point, ce qui fausse la construction. Le rayon de sélection réglable de CaRMetal est un avantage pour ces élèves maladroits.
Voici le corrigé en ligne de ce TP :
Lorsque le point qui laisse une trace se déplace à l’écran, on voit apparaître la représentation graphique d’une fonction que plusieurs élèves identifient comme « une fonction homotruc », alors qu’en général ils sont complètement bloqués sur les fonctions (manque total de connaissances sur le vocabulaire des fonctions, impression que les fonctions sont trop abstraites par exemple). Il s’agit plutôt d’une reconnaissance de forme que d’un problème d’analyse, mais historiquement, la notion de représentation graphique semble avoir précédé celle de fonction (mathématique).
Ci-dessous on peut télécharger (au format diaporama CaRMetal) la démonstration du fait que les deux fonctions sont effectivement homographiques.
Voir aussi un autre exemple de fonctions homographiques traité en Seconde.
Une application à la transformation de Laplace
La transformée de Laplace d’une fonction $f$ est un objet un peu complexe : On commence, à partir de $f(x)$, par définir une fonction de deux variables $x$ et $p$, égale à $f(x) e^{-px}$ ; puis on intègre cette fonction de 0 à $+\infty$, définissant $\mathcal{L}f(p)=\int_{0}^{+\infty}f(x) e^{-px} \mbox{d}x$ ! Le fait que cette intégrale puisse être une fonction de p peut surprendre l’élève qui s’est perdu dans ce labyrinthe d’abstractions successives ; la technique vue ci-dessus peut l’aider à concevoir cela, en représentant ladite fonction.
Le principe de la manipulation est d’introduire l’intégrale, non comme une fonction, mais comme une « expression » de CaRMetal.
- Tout d’abord, on crée une « fonction définie par l’utilisateur » égale à f(x) (la fonction à transformer) ; dans l’exemple ci-dessous on a choisi la fonction de Heaviside max(x,0).
- Ensuite on crée un point M sur l’axe des abscisses ;
- puis on crée une expression p égale à l’abscisse x(M) de M ;
- ensuite on crée la fonction ici appelée g égale f(x)*exp(-p*x) (en réalité, g est un représentant d’une famille de fonctions paramétrée par p)
- enfin, l’expression L (la transformée de Laplace) est l’intégrale de g de 0 à 16 (qui a été choisi ici comme approximation de l’infini) :
Enfin, on crée un point de coordonnées (u ;L) et on « active sa trace ». En bougeant M, on voit que ce point parcourt une courbe, qui représente graphiquement une fonction de p :
La transformée de Laplace d’une fonction de x est donc une fonction de p (ci-dessus, l’inverse de p, qui est d’ailleurs une homographie aussi).
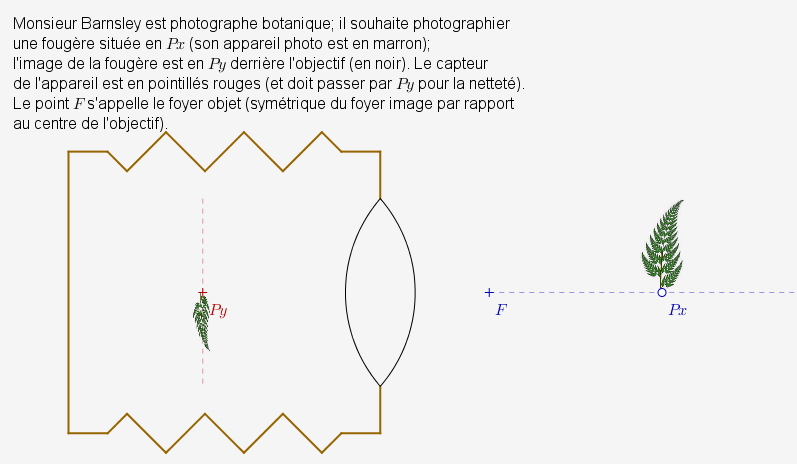
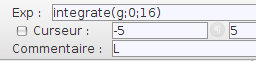
Commentaires