Construction du tétraèdre

Pour une fois, on ne perd pas en généralité en supposant le tétraèdre régulier. Alors après avoir créé une nouvelle figure 3D de CaRMetal, on sélectionne l’icône « tétraèdre régulier » et on choisit l’origine du repère comme centre. Il apparaît alors une expression « k=2 » (taille du tétraèdre) qu’on rend invisible (outil « gomme »).

Les points I et J (en vert) ont été créés avec l’outil « milieu » et L (en marron) avec l’outil « translation » :

doc=2589>

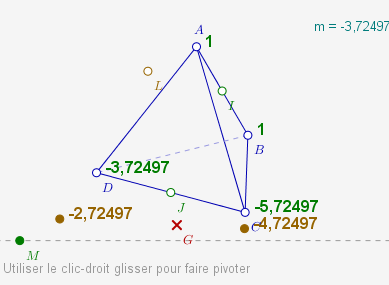
Pour obtenir un réel m variable, on a créé la droite d’équation y=-2 (en noir) et placé un point M (en vert) sur cette droite. m est alors l’abscisse de M.

Le fait que la droite est fixe par rapport au repère du plan la fait bouger si on fait tourner le tétraèdre. Sinon c’est M qui aurait bougé. Ce n’est pas gênant pour construire ou conjecturer.

Ci-dessous on a juste créé une expression m égale à x(M).

Barycentres

La suite est basée sur le fait que la perspective cavalière conserve le barycentre. CaRMetal n’ayant pas de macro pour les barycentres de 4 points, on commence (après avoir affecté les masses 1, 1, m-2 et m aux points A, B, C et D avec la macro « point pondéré ») par construire (avec la macro « barycentre de deux points affecté de la somme des masses »)

• le barycentre de A(1) et D(m) affecté de la masse m+1 ;
• puis le barycentre de B(1) et C(m-2) affecté de la masse m-2+1=m-1.

Alors G est le barycentre de ces points pondérés :

C’est en modifiant m par le mouvement de M qu’on peut émettre les deux conjectures du 2.a et du 2.b.

Lieu de G

La construction du lieu est aisée : On sélectionne l’outil « lieu », puis on clique sur le point G et on double-clique sur le point M :

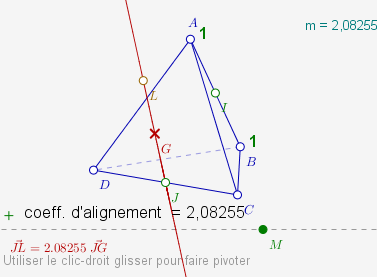
Colinéarité

La macro « coefficient d’alignement » de CaRMetal permet de conjecturer l’alignement de G, J et L et la relation de colinéarité entre les deux vecteurs (après avoir gommé les masses des points pondérés) :