L’exercice 4 « obli » du sujet de Pondichéry 2017 commençait ainsi :

On considère deux suites (u_n) et (v_n ) :
• la suite (u_n) définie par u₀ = 1 et pour tout entier naturel n : u_n+1 = 2u_n − n + 3 ;
• la suite (v_n) définie, pour tout entier naturel n, par v_n = 2ⁿ.

Il ne s’agit pas de somme mais c’est l’occasion de comparer l’outil suites de la calculatrice avec l’outil de programmation. On se concentrera notamment sur la question :

B 3. Déterminer le rang du premier terme de la suite supérieur à 1 million.

Comme le suggère le titre de cet article, c’est la calculatrice Numworks qui a été choisie pour ce comparatif, puisqu’elle se programme en Python.

L’écran de la Numworks ressemble à celui d’un smartphone, avec des icônes, chacun menant à une page web. On navigue dans ces pages comme sur le smartphone. L’icône des suites se trouve en haut à droite :

Une fois atteint cet icône à l’aide des flèches du clavier, on appuie sur OK et on a la possibilité d’ajouter une suite à une liste de suites actuellement vide :

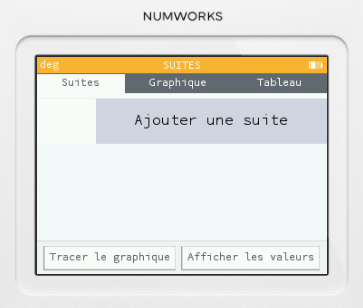
En appuyant sur OK, on a le choix entre suites explicite et récurrente :

On choisit la suite récurrente et on entre d’abord la formule :

L’appui sur OK montre qu’à l’édition la notation indicielle devient u(n). Ce qui permet d’entrer la formule :

Ensuite on entre, par une méthode similaire, le premier terme :

Et on ajoute une nouvelle suite, celle-ci de type explicite :

On utilise le bouton x^y pour entrer le chapeau :

Et voilà, il n’y a plus qu’à naviguer vers l’onglet « tableau » :

Le tableau donne les mêmes informations que celui de l’énoncé (obtenu lui par un tableur, c’est un peu nouveau au bac S) :

Pour répondre à la question B3, il suffit (après avoir redéfini le rang), de naviguer un peu dans ce tableau :

Ce serait bien que la navigation puisse être rendue automatique par une option de la calculatrice, mais pour l’instant ce n’est pas le cas, la priorité allant à la version Python (ci-contre).

Par contre on a aussi le graphique, moins facile à faire avec Python :

La navigation dans le nuage de points se fait avec les flèches.

L’application permettant de programmer est tout à droite, en bas :

En la sélectionnant, on a (après un message prévenant qu’il s’agit d’une version beta) le choix entre « éditer » et « exécuter » le programme Python (il n’y en a qu’un mais pour une calculatrice destinée à être utilisée en mode examen c’est plutôt logique). On choisit d’abord « éditer » et on entre ce programme :

u=1
for n in range(1,12):
    u=2*u-n+4
    v=2**n
    print(n,u,v)

Comme on commence par 1, on a un décalage et c’est 4 qu’on additionne, et non 3. Avec le bouton « OK » on peut exécuter ce programme ce qui a pour effet d’afficher n, u et v :

Partie 3

Pour la troisième partie, on ne peut utiliser pour l’instant que le programme Python, parce que pour l’instant, on ne peut pas définir de récurrence croisée dans l’outil des suites. Mais avec Python c’est facile, il suffit d’afficher u/v au lieu d’afficher u et v :

Pour ceux qui veulent tester ce script sur une autre version de Python :

u=1
for n in range(1,12):
    u=2*u-n+4
    v=2**n
    print(u/v)

La conjecture sur la limite de u/v se fait avec l’affichage obtenu :

Pour la question B3, on modifie le programme Python en changeant le style de boucle :

u=1
n=0
while u<1e6:
    u=2*u-n+4
    n=n+1
print(n)

L’exécution de ce script répond à la question 3B :

L’exercice 3 du sujet Amérique du Nord 2017 était basé sur des égalités entre sommes et produits, ce qui lui donne un intérêt mathématique certain :

Le but de cet exercice est d’étudier les suites de termes positifs dont le premier terme u₀ est strictement supérieur à 1 et possédant la propriété suivante : pour tout entier naturel n>0, la somme des n premiers termes consécutifs est égale au produit des n premiers termes consécutifs.
On admet qu’une telle suite existe et on la note (u_n). Elle vérifie donc trois propriétés :
• u₀ > 1,
• pour tout n > 0, u_n > 0,
• pour tout n > 0, u₀ +u₁ +··· +u_n−1 = u₀ ×u₁ ×··· ×u_n−1.

1. On choisit u₀ = 3. Déterminer u₁ et u₂.

Cette question avait le double mérite de vérifier les connaissances des candidats en équations du premier degré, et de montrer le principe de la suite de l’exercice : Le fait qu’il y a égalité entre produit et somme aboutit à ce que le terme suivant de la suite u est solution d’une équation du premier degré, une fois les termes précédents connus, et on le trouve alors par une relation de récurrence :

2. Pour tout entier n > 0, on note s_n = u₀+u₁ +··· +u_n−1 = u₀×u₁ ×··· ×u_n−1.
On a en particulier s₁ = u₀·
a. Vérifier que pour tout entier n > 0, s_n+1 = s_n+u_n et s_n > 1.
b. En déduire que pour tout entier n > 0,
u_n = s_n/(s_n −1).
c. Montrer que pour tout n > 0, u_n > 1.

Le c se démontre évidemment par récurrence, et le b est la même question que la 1, mais dans le cas général : On résout l’équation du a. Mais le point ici est le a :

s_n+1 = s_n+u_n

Cette formule de récurrence, apparemment censée être connue des élèves de terminale S, est à la base de l’algorithme de sommation suivant :

• on initialise la variable s à 0 ;
• après chaque mise à jour de la variable u, on additionne celle-ci à s, avec le s ← s+u de rigueur : C’est une traduction algorithmique de la formule récurrente ci-dessus.

À l’aide de l’algorithme, on veut calculer le terme u_n pour une valeur de n donnée.
a. Recopier et compléter la partie traitement de l’algorithme.
b. Le tableau ci-dessous donne des valeurs arrondies au millième de u_n pour différentes valeurs de l’entier n :

Quelle conjecture peut-on faire sur la convergence de la suite (u_n) ?

La suite de l’exercice visait à prouver la conjecture, en passant par le fait que s_n diverge (on montre par récurrence qu’elle est minorée par n) et que du coup, u_n converge. Mais voyons un peu l’algorithme :

Les scripts ci-dessous ont été obtenus à l’aide de cet outil en ligne.

Dans la nouvelle notation, il n’y a plus que « la partie traitement » et l’algorithme se rédige ainsi :

s ← u
Pour i allant de 1 à n 
    u ← ...
    s ← ...
Fin Pour

Le source Python donne cette variante :

u ← 3
s ← u
pour i allant de 0 à n-1
        u ← s/(s-1)
        s ← s+u

Le source étant

u = 3
s = u
for i in range(n)
        u = s/(s-1)
        s = s+u

Mais aussi, cette variante permet d’avoir un code plus sofusien :

u = 3
s = u
for i in range(n)
        u = s/(s-1)
        s += u

Le résultat :

u ← 3
s ← u
pour i allant de 0 à n-1
        u ← s/(s-1)
        augmenter s de  u

En général, la série se calcule à partir de la suite avec l’algorithme de sommation. Mais ici la suite n’est pas définie indépendamment de la série.

On remarque que dans ce cas, il est possible de calculer les termes successifs de u_n parce qu’on dispose de l’expression de u en fonction de s : Les suites u et s sont définies par une récurrence croisée. L’abondance d’exercices au bac S 2017 sur les récurrences croisées explique probablement que celles-ci sont reconnues depuis peu par la Ti 83 Premium CE (mais pas encore par la Numworks à ce jour, bien que la demande en ait été faite).

Le calcul itératif d’une factorielle se fait ainsi en Python (ici on se contente de 10 termes) :

p = 1
for k in range(1,11):
    p = p*k
    print(p)
    

Ce qui donne ce pseudocode (p est la variable contenant la suite des factorielles) :

p ← 1
pour k allant de 1 à 10
    p ← p×k
fin du Pour

Version Sofus

Pour additionner les inverses des factorielles, il suffit alors de faire pareil avec la variable additionnelle s, à laquelle on ajoute au fur et à mesure les 1/p :

p ← 1
s ← 1
pour k allant de 1 à 10
    p ← p×k
    s ← s+1/p
fin du Pour

p = 1
s = 1
for k in range(1,11):
    p = p*k
    s = s+1/p
    print(s)

Avec Sofus, cet algorithme se programme ainsi :

Et SofusPy permet, à partir de ce programme, d’engendrer automatiquement le code Python qui sera peut-être présent dans le sujet de BTS.

On pouvait aussi, assez facilement, faire le TP avec un tableur, en mettant dans la première colonne les valeurs de n, dans la seconde celles des factorielles (formule du genre =B1*A2 à copier vers le bas) et dans la troisième, les valeurs de la suite (formule du genre =C1+1/B2).

Le TP n’a duré qu’une heure et ce n’est pas tout le monde qui a trouvé le temps d’améliorer la rédaction à la maison. Outre des rapports jamais déposés sur Moodle, il y a eu certains assez incomplets :

largement inachevé	hostile au texte écrit	amateurs de pseudocode	choix de Sofus

Ce rapport témoigne du choix d’Algobox pour programmer les algorithmes (ce qui est une très bonne idée) mais aussi de celui de se contenter d’en faire une copie d’écran (mauvaise idée, c’est tout flou donc peu lisible) au lieu d’exporter la version textuelle pour ensuite l’incorporer au document :

Ces copies d’écran floues ne sont pas caractéristiques des utilisateurs d’Algobox, ceux de CoffeeScript aussi :

Ce rapport montre un travail de mise en forme et en couleurs, hélas pas assorti de rédaction de textes :

Celui-là est entaché d’une erreur : Au lieu d’incorporer le fichier svg dans le traitement de texte, a été choisi un simple lien vers l’original, ce qui allège l’odt mais ne permet pas d’afficher la figure dans le pdf exporté :

Le svg est bien affiché dans celui-là mais là encore, peu de texte :

Il y avait quand même plusieurs (très) bons rapports de TP ; leur description ci-dessous indique ce qu’il leur manque :

critique	définition de e	critique	critique	conclusion	rien (parfait)

Voici le corrigé, avec son source au format odt :

corrigé en pdf	source en odt

La calculatrice Numworks permet, rien qu’avec son application Sequence, de calculer la somme de termes, en choisissant les indices de départ et d’arrivée [4].

Une fois dans l’application des suites, il faut trouver la factorielle : C’est encore la partie la plus difficile :

Oui, le bouton à appuyer est celui qui ressemble à une boîte aux lettres, le deuxième en partant de la droite ci-dessus : En fait il représente une boîte à outils, et parmi ces outils se trouve le nombre de manières de permuter r objets parmi n, ici en prenant r=n on a la factorielle...

Après cela, la suite des inverses de factorielles se dessine directement :

Le tableau de valeurs montre qu’il n’y a que 10 valeurs calculées :

Mais en allant tout en haut de ce tableau, on voit un régler l’intervalle qui permet d’aller plus loin, par exemple jusqu’à 40 :

Ensuite, en réaffichant le nuage de points, on voit un bouton OK en bas à droite de l’écran. Il donne envie d’appuyer sur la touche OK et là, divine surprise, est proposé de calculer la somme des termes :

Le choix de cette option réaffiche le nuage de points avec la possibilité de naviguer avec les flèches du clavier mais cette fois-ci c’est pour choisir l’indice du premier terme à additionner ; on va jusqu’à l’abscisse 0 et on appuie sur OK puis est demandé l’indice du dernier terme à additionner (ici provisoirement 9) :

En allant jusqu’à 20 on voit en bas à gauche que la Numworks est prête à additionner les 21 premiers termes :

L’appui sur la touche OK permet alors d’avoir une valeur approchée de e sans avoir eu à programmer le moindre algorithme :

Hors programme, le sujet est intéressant par sa démonstration graphique : On calcule ln(n) comme intégrale, entre 1 et n, de la fonction 1/x ; puis on approche l’aire sous l’hyperbole par un histogramme (rectangles de largeur 1 et de hauteur 1/n). Plutôt que représenter les deux suites sur un même graphique pour constater leur décalage, il a été préféré de représenter carrément leur différence. Peu d’étudiants ont su conjecturer la convergence de cette différence sur la représentation graphique. Cela témoigne d’un manque d’expérience sur les représentations graphiques des suites.

Le calcul intégral n’a d’ailleurs pas encore été abordé en cours.

Ces deux rapports sont un plaidoyer pour l’utilisation du tableur à la place des algorithmes. Sur la forme ce plaidoyer n’est pas très réussi, on voit même une copie d’écran de toute la feuille du tableur juste pour montrer la formule utilisée :

trop concis	très bon !

Ce rapport cherche à montrer l’intérêt d’Algobox ; sans grand succès en raison du flou rendant illisible l’algorithme [5] :

Les rapports de TP suivants se terminent par l’émission d’une conjecture non prévue : La décroissance (à partir du rang 2) de la suite ; c’était la convergence qui était attendue :

plutôt décroissante	devient décroissante et n’est plus croissante

Les rapports de TP suivants méritent à eux seuls la lecture de cet article, en effet ils témoignent à la fois du progrès réalisé depuis le TP précédent, et des difficultés à conjecturer la convergence [6], et surtout à la verbaliser :

conjecture mal verbalisée	γ=0	γ=0,5	γ=0,599

Voici le corrigé du TP, fait avec alcoffeethmique :

corrigé en pdf	source en odt