Sur la capture d’écran ci-dessous, on aperçoit le héros du jeu, surnommé « Blackball », qui au départ était à gauche, et a été déplacé jusqu’à ce qu’il touche la pierre bleue.

Celle-ci avait initialement l’aspect des autres pierres bleues appelées « oxydes » et donc surmontées de pyramides. Mais au contact de Blackball, la pyramide s’est ouverte, révélant un carré bleu clignotant (on ne voit pas le clignotement sur la capture ci-dessus). On comprend alors qu’il s’agit pour Blackball d’aller toucher les autres oxydes pour les ouvrir, par exemple à droite :

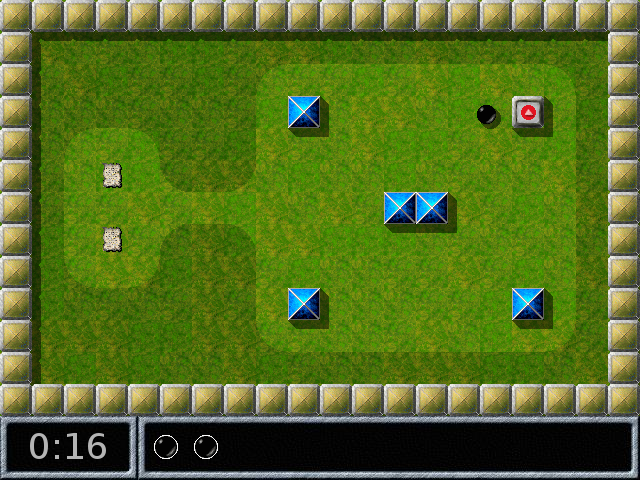
Cette fois-ci, la pierre est rouge, et en s’ouvrant elle a fermé l’oxyde précédente : Une seule oxyde à la fois peut être ouverte. Comment alors peut-on les ouvrir toutes ?

On voit ci-dessus une exception à la règle précédente : C’est parce que la deuxième oxyde est rouge aussi que Blackball, en les activant toutes les deux, a établi une sorte de lien télépathique entre ces deux oxydes et qu’elles restent ouvertes définitivement.

On découvre alors une autre règle d’Enigma : Les oxydes sont toujours en nombre pair, et le but du jeu est de les ouvrir en séquence jusqu’à ce qu’elles soient toutes ouvertes, ce qui nécessite de la mémoire à court terme.

Une caractéristique qu’Enigma a hérité de son ancêtre Oxyd est l’aspect atextuel du jeu : D’abord on cherche à comprendre ce qu’on doit faire, ensuite à comprendre comment on va le faire.

Le titre de cet article fait allusion à un mystère : Comment un jeu aussi simple peut-il avoir autant de fans ? C’est que dans l’exemple ci-dessus, Blackball peut rouler sur l’herbe dans tout l’écran, sauf aux bords qui sont fermés par des pierres, et que rien ne gêne son accessibilité aux oxydes. Il est possible pour les concepteurs de ce jeu de disposer sur le terrain des obstacles, et aucune limite ne semble exister pour la complexité des niveaux d’Enigma...

Ce paysage est très aquatique : Blackball est naufragé sur un îlot de forme rectangulaire, avec pour toute richesse 4 caisses de bois, et voit 3 oxydes (un nombre impair : C’est un indice, il y en donc forcément une autre quelque part, invisible sur l’écran), cette fois-ci sans leurs pyramides, mais l’une est en pleine mer et les autres sur des autres îlots :

Pour essayer d’atteindre celle du bas à gauche, Blackball essaye de nager vite vers l’îlot en question :

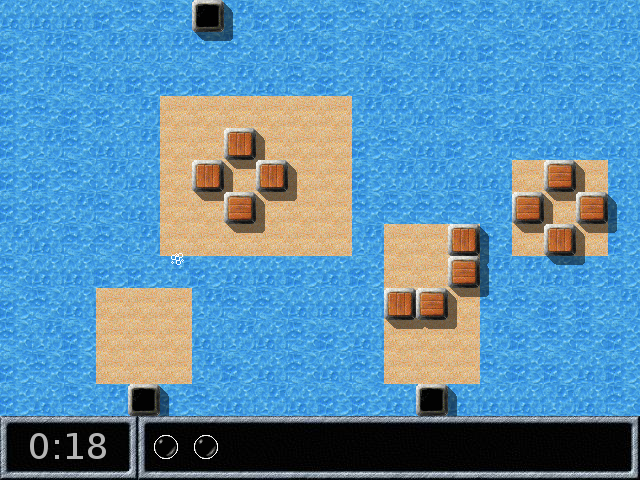
Le problème c’est que Blackball ne sait pas nager même sur une distance aussi courte, on ne voit plus de lui qu’un chapelet de bulles. Il va donc falloir essayer autre chose. Comme par exemple se taper la tête contre les murs, ou plutôt les caisses de bois :

La caisse a bougé ! On constate que Blackball a ressuscité mais qu’en bas, au lieu des deux vies supplémentaires dont il disposait au début, il ne lui en reste plus qu’une. En faisant le tour, il peut pousser la caisse vers le bas

puis dans l’eau :

(on constate que suite à une fausse manœuvre il s’est malencontreusement noyé à nouveau, et qu’il n’a maintenant plus de vie supplémentaire. En effet jouer à Enigma requiert parfois de l’habileté).

Il dispose maintenant d’un passage vers la première oxyde :

Comme il lui reste des caisses de bois pour fabriquer d’autres ponts, il peut maintenant accéder aux autres oxydes de l’écran et aux autres écrans (la quatrième oxyde, invisible ici, il faut bien qu’elle soit quelque part...).

En plus des oxydes de ce jeu, il y a de fausses oxydes, en effet en touchant l’une des pierres qui délimitent le fort ci-dessus, blackball n’a réussi qu’à l’allumer en rouge foncé, sans révélation du motif coloré habituel. Les vraies oxydes doivent donc être inaccessibles, protégées par la douve visible en haut à droite.

Comme dans l’onglet précédent, on peut combler cette douve avec les trois caisses de bois, à condition de ne pas coincer celles-ci dans un coin (elles peuvent être poussées mais pas tirées) :

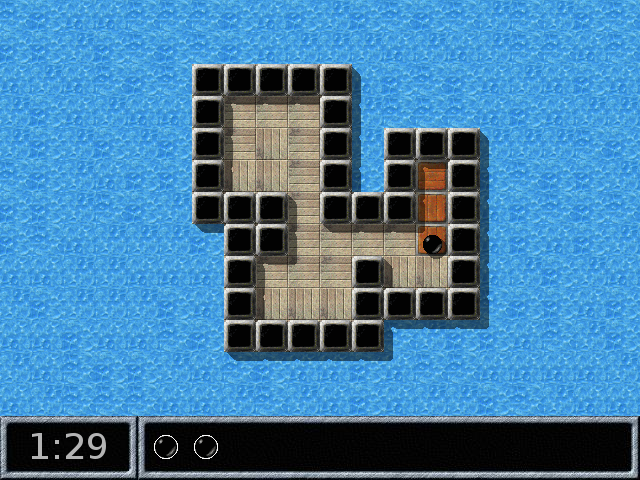
Il y a bien des oxydes tout au fond :

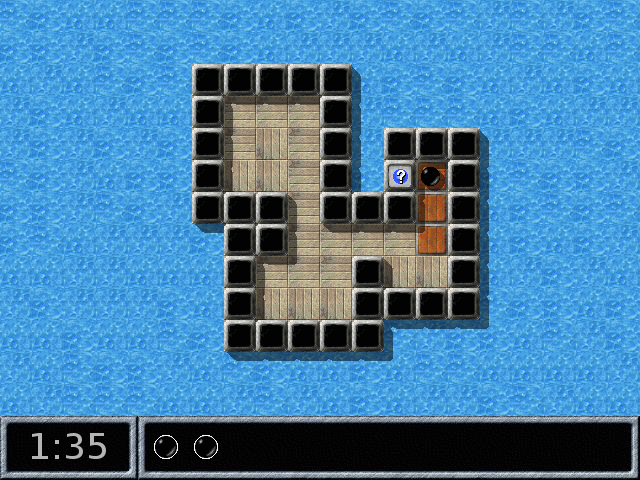
Au moment précis où on gagne l’écran ressemble à ceci :

Des explications sur le PAR figurent dans l’onglet « Algorithmique ».

Ce jeu est une légère variante de Sokoban (en effet dans Sokoban, l’ordre dans lequel on place les caisses sur leur emplacement n’a pas d’importance, alors qu’ici on est obligé de fabriquer le pont de bas en haut). Parmi le millier de niveaux d’Enigma actuellement disponibles, plus de 300 sont des Sokoban, en général importés de la collection libre de David Skinner.

Dans un registre analogue, plusieurs niveaux d’Enigma sont des puzzles à base de pentaminos, et leur nombre est destiné à s’agrandir énormément dans la version 1.10.

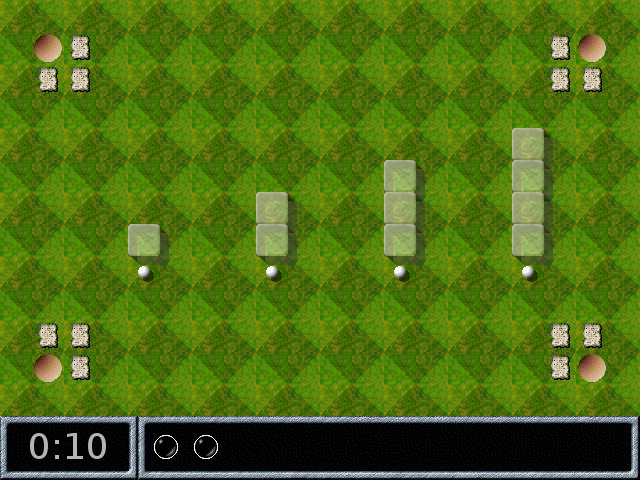
Dans ce niveau il n’y a ni oxydes ni Blackball. On aperçoit 4 creux dans les coins et 4 billes blanches qui suivent toutes les 4 les mouvements de la souris. On devine que le but du jeu est de caser chaque bille blanche dans un creux. Ce genre de niveau se réussit parfois très vite mais à condition de les jouer lentement, ce qui leur a valu le nom de « Meditation ». Celui-ci se trouve dans « Esprit ».

Ce niveau de méditation est particulier dans le sens où, ici, les billes blanches sont numérotées (par les colonnes de pierres qui les surplombent). Autour de chaque creux il y a des documents que les billes blanches peuvent ramasser tout simplement en roulant dessus. Par exemple si la bille numéro 1 roule sur un document en bas à gauche, en cliquant n’importe où, le texte du document défile en bas :

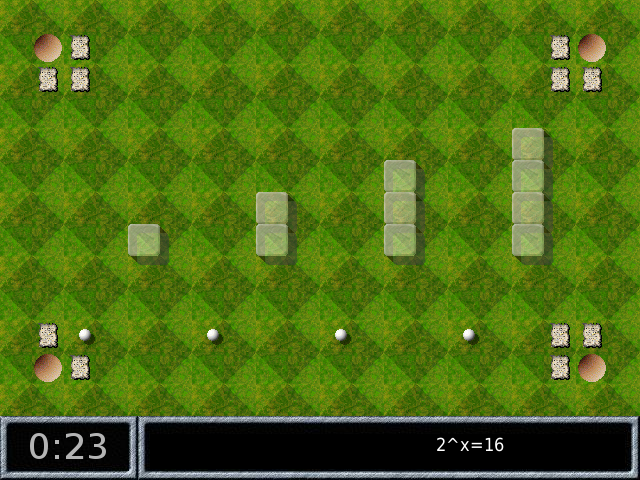
C’est une équation ! Celle-ci est de niveau collège, et demande quelle puissance de 2 est égale à 16. On en déduit que c’est la bille numéro 4 qui doit aller dans ce creux (encore un jeu de mémoire). Le creux en bas à droite dit ceci :

Cette fois-ci c’est une expression à calculer mais elle aussi est de niveau collège. Le creux en haut à gauche dit ceci

et le dernier

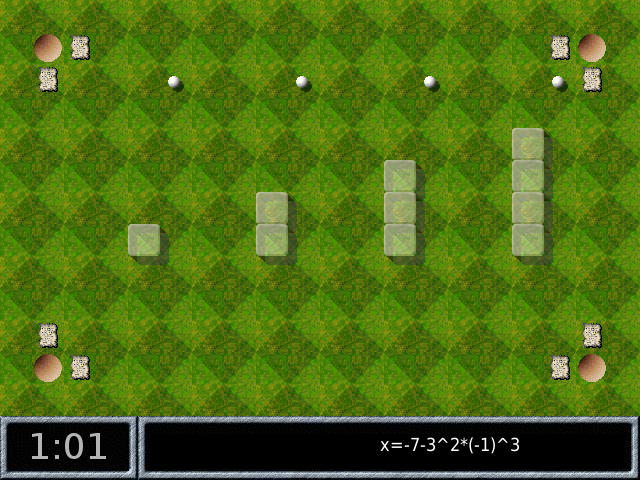
Pour finir ce niveau il ne reste plus qu’à se rappeler quelle bille va dans quel creux (c’est pour ça que dans les images ci-dessus on a pris soin de ne pas les mélanger) et dès que la dernière rentre dans son creux, elles disparaissent en même temps :

Quelques explications sur le PAR figurent dans l’onglet « algorithmique ».

• Enignimm est un des jeux de Nim peu classiques.
• Map it out est un labyrinthe bidimensionnel où les connections entre salles ne sont pas visibles, mais dans la version 1.10 d’Enigma il y aura un Map it out II où le labyrinthe est quadridimensionnel. Dans la même version il y aura des jeux basés sur les graphes, dont un où le but de jeu est précisément de colorier, au sens propre, un graphe. Il y aura aussi une version assez difficile du jeu des chiffres et des lettres.
• Use The PIN est un labyrinthe basé sur une suite de chiffres bien connue...
• Control Panel est basé sur l’écriture binaire des ombres entiers.
• Sierpinski est basé sur l’exploration d’une approximation de la courbe de Koch quadratique, que Benoît Mandelbrot appelle flocon de Neige de Sierpinski.
• Enigris est une implémentation du jeu Tetris en Enigma.
• Laser splitting est un jeu dont le but est de construire une approximation finie d’une courbe de Peano.
• The cube est un Rubik’s cube représenté sous forme d’un patron de cube.

Le superbe niveau The Metapuzzle ressemble à de l’algorithmique parce qu’au lieu de le résoudre directement, on utilise une machine fabriquant des outils de son choix :

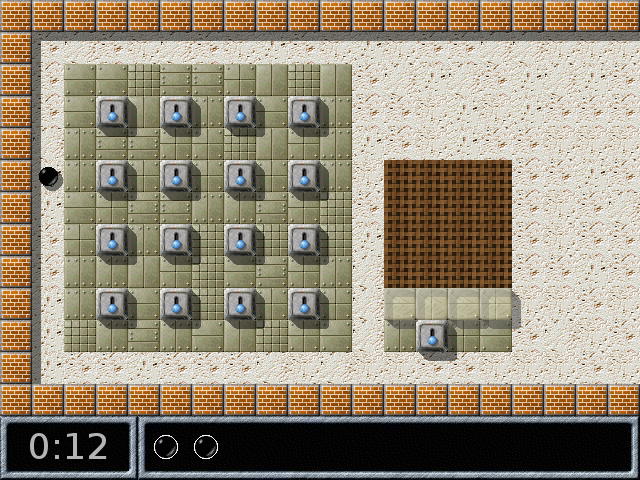
La grille d’interrupteurs à gauche est une matrice booléenne, chaque interrupteur allumé (position : en haut) déterminant une des pièces du puzzle fabriqué par la machine (d’où le titre du niveau). Par exemple, si on actionne les deux interrupteurs en haut à droite :

L’action de l’interrupteur du bas occasionne la création d’une pièce composée de deux carrés (si le motif n’est pas connexe ça ne marche pas) :

Et on peut pousser ce motif en le heurtant suffisamment fort avec la boule noire :

En le poussant suffisamment loin, on arrive à l’écran de droite, où on peut apercevoir des outils à ramasser : Un ressort pour bondir, et un marteau qui sert à casser les pierres fissurées qui empêchent l’accès aux oxydes. Mais tout ça est inaccessible à cause de l’abîme (en noir) qui a le même effet que l’eau : Impossible de le traverser :

Blackball ne peut traverser la zone noire (il tombe dans un vide sans fin) mais la pièce de puzzle, elle, peut combler ce vide :

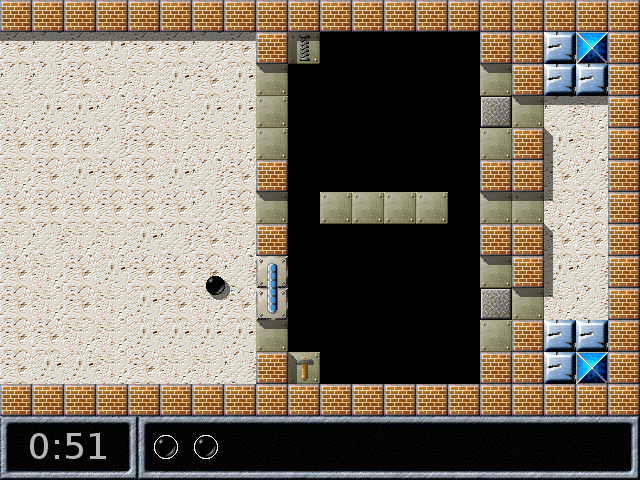
Encore une poussée, et

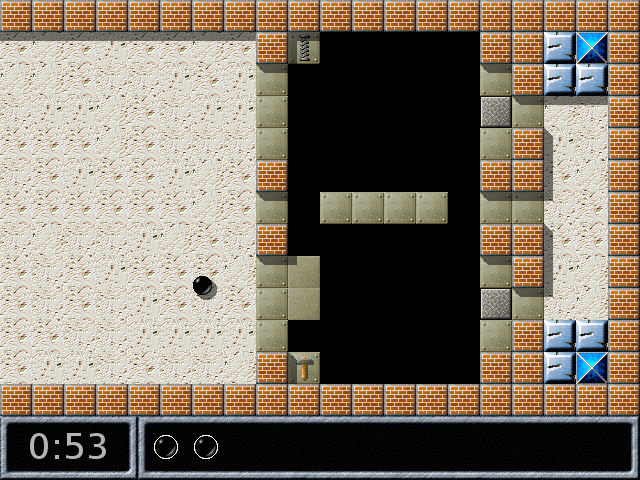
En répétant l’opération, on peut accéder au marteau, puis au ressort, et à l’autre côté. Mais ce n’est pas si facile, le mieux est encore de jouer à ce niveau pour découvrir pourquoi...

Le plus intéressant de ce niveau du point de vue algorithmique, c’est sa métadescription, en l’occurence le code source de ce niveau, lisible ici, avec une belle coloration syntaxique : La partie en rouge est une carte du niveau, et la fabrication des pièces de puzzle est effectuée par la fonction finalize_puzzle qui construit une chaîne de caractères (la concaténation de chaînes se fait avec deux points « .. ») décrivant la pièce de puzzle puis ajoute le résultat dans le tableau des objets du jeu. Autrement dit, c’est un programme Enigma qui construit un programme Enigma...

• Enigmastermind est une implantation du jeu de Mastermind en Enigma.
• Puzzling controls est un jeu où le joueur doit programmer une sorte de tortue LOGO invisible pour qu’elle aille aux bons endroits.
• The Turtle aussi, à ceci près que la tortue est visible. Ce jeu peut donc lui aussi être considéré comme une introduction à l’algorithmique.
• Khun Phan est une implémentation de l’âne rouge en Enigma.
• The life Game est un jeu basé sur le jeu de la vie de John Conway.
• et surtout, le jeu Print23 consiste pour le joueur à écrire un programme dans le langage de programmation Brainfuck, un langage ne connaissant que 7 instructions (plus une instruction d’entrée non utilisée ici), lequel programme est chargé d’écrire 23. Ce niveau d’Enigma est donc un interpréteur Brainfuck complet :

Les instructions du langage sont choisies avec les 7 interrupteurs de gauche, les deux autres servant respectivement à effacer la dernière instruction entrée, et à exécuter le programme. Le programme s’affiche dans la fenêtre du bas (et est donc limité à 28 instructions).

Par exemple, le programme

++++>++

met 4 dans la première variable, puis 2 dans la deuxième :

ce que confirme l’affichage du débogueur de l’interpréteur.

La multiplication de 8 par 7 se fait avec le programme

>+++++++[<++++++++>-]

(on commence par aller à la deuxième variable, que l’on rend égale à 7 ; puis on effectue une boucle, 7 fois donc, où on recule vers la première variable, que l’on incrémente 8 fois, et on retourne à la deuxième variable que l’on décrémente ; comme on quitte la boucle lorsque la deuxième variable est nulle, on l’effectue bien 7 fois).

Le message de débogage confirme bien que la première variable est égale à 56 et la deuxième est nulle à la fin du programme :

Ceci dit ce jeu est loin d’être simple, parce que non seulement 23 est premier, mais pour l’afficher il faut utiliser le code ASCII qui consiste à additionner 48 à chacun de ses chiffres ; c’est donc un 50 et un 51 que doivent contenir les deux variables...

Et pour ce qui est de l’utilisation de ce langage pour l’apprentissage de l’algorithmique, elle est peu recommandée vu que le langage est peu lisible et utilise les tableaux et les pointeurs, hors programme.

Le calcul du PAR (pour Professional Average Rating), un terme hérité du golf, donne lui aussi un exemple de démarche algorithmique : Le PAR se calcule à partir des durées des joueurs dit « professionnels », c’est-à-dire ceux qui ont enregistré auprès du site d’Enigma plus d’une centaine de niveaux réussis ; ce sont ceux qui ont un « handicap ». Or bien qu’average signifie moyenne, ce n’est pas la moyenne des durées qui est calculée mais la moyenne harmonique de celles-ci : En effet plus la durée est courte et plus le joueur est bon. Un paramètre plus pertinent que la durée pour classer les joueurs est donc l’inverse de celle-ci, d’où la moyenne harmonique. Celle-ci est décrite dans le manuel d’Enigma comme une moyenne coefficientée donnant plus de poids aux bons joueurs qu’aux moins bons :

(extrait du manuel de référence d’Enigma)

Le jeu Enigma est écrit dans le langage de programmation Lua, qui ressemble un peu au défunt Pascal, mais avec des objets. En Lua, une boucle s’écrit « for i=1,10 do ... end » et un test « if x==2 then ... else ... end » ce qui rend ce langage assez lisible pour toute personne ayant des rudiments d’Anglais. Pourtant, le langage Lua est brésilien. Un interpréteur en ligne est ici.

Lua est d’ailleurs un des langages favoris des amateurs de jeux, surtout les jeux de rôles et les jeux sur console. Ce qui évidemment lui donne un attrait immense auprès des élèves de Seconde...

La création d’un jeu sous Enigma est donc assez facile en mode texte, et d’ailleurs ce faisant, on s’amuse encore plus qu’en jouant à Enigma (ceci est un témoignage personnel...) ! Et avec le logiciel BlackBall Editor il suffit de dessiner le jeu avec la souris pour concevoir celui-ci !

Il se trouve que justement, la conception de jeux vidéos soulève des problèmes d’algorithmique intéressants (et pas toujours simples), comme par exemple le comptage des jeux de Nim.

Des exemples propres à Enigma :

• Comme les objets d’Enigma (à part Blackball) ont des coordonnées entières, la recherche des voisins les plus proches d’un objet donné utilise la distance de Manhattan.
• Les calculs de coordonnées et les tests sont utiles en Enigma ; par exemple pour savoir si Blackball est au point de coordonnées (3,5) on écrit

  if Blackball.x == 3 and Blackball.y == 5

• Un bon moyen de trouver un arbre de poids minimum est l’algorithme de Kruskal. Nat Pryce a réussi à le convertir en un générateur automatique de labyrinthes, les labyrinthes étant des objets importants dans Enigma. Cet algorithme, récursif, fonctionne par décomposition et recomposition, avec une réunion de sous-labyrinthes : -- Union-find algorithm for merging "zones" of the maze. Each zone is -- a tree of cells identified by the cell at the root of the tree. A root -- cell is represented by a nil reference in the zones table indexed by the -- cell number. function find_zone( zones, cell ) if zones[cell] == nil then return cell else zones[cell] = find_zone( zones, zones[cell] ) return zones[cell] end end function union_zones( zones, cell1, cell2 ) zones[find_zone(zones,cell2)] = find_zone(zones,cell1) end

  (extrait de la bibliothèque « natmaze » en Lua). Un exemple de labyrinthe engendré automatiquement peut se voir ici.

• De même, des objets de type « puzzle » peuvent être engendrés automatiquement par une biliothèque Lua qui assure que, après permutations, le puzzle obtenu est connexe. Les manipulations de ces objets, comme le Rubik’s cube, utilisent beaucoup des conjugaisons dans le groupe des permutations. Un exemple d’utilisation de cet algorithme est ici.
• Enigma possède des objets qui interagissent comme le « trigger » qui réagit lorsque Blackball roule dessus (on en voit à droite dans Metapuzzle dans l’onglet précédent), ou les interrupteurs. Ceux-ci communiquent avec d’autres objets (allumage d’un laser ou ouverture d’une porte par exemple). C’est une manière originale de présenter les notions de programmation objet ou de sous-programme (l’action d’un interrupteur appelant le sous-programme).