Les routes de Monsieur Fermat avec CarMetal et Scratch

Une application de l’inégalité triangulaire

mardi 26 octobre 2010
par Nathalie CARRIÉ

Comme cette année la valeur absolue est une nouveauté dans le programme de première S et comme elle n’est pas encore traitée dans les manuels, la conception de ce chapitre pour mes élèves m’a menée à une réflexion sur distance et algorithmes, pour finalement leur proposer le problème des autoroutes de Fermat que j’avais lu dans le manuel ISTRA de l’IREM de Strasbourg [1].

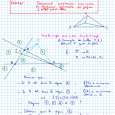
Voici le plan du cours que j’ai proposé à mes élèves. Le cours manuscrit en classe à l’aide du logiciel Xournal se trouve dans le portfolio ci-dessous. [2]

Définition
définition algorithmique de la valeur absolue et définition mathématique
Distance
- distance sur une droite
  résolution d’équations et d’inéquations simples avec la valeur absolue
- Distance dans le plan
  calcul avec algorithme et programme TI82
- Equations de cercles
Inégalité triangulaire
- avec des nombres réels
- avec des points
Application : le problème de Fermat.

Le problème de Fermat

Enoncé du problème posé par FERMAT :

Étant donné 3 villes A, B, C au sommet d’un triangle, il s’agit de construire une route de longueur minimale reliant les 3 villes 2 à 2.

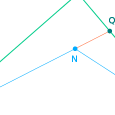
– Lemme préliminaire

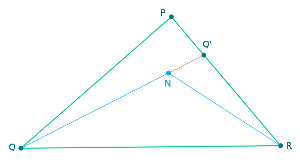
PQR est un triangle.
Pour tout point N intérieur au triangle, on a : $NQ+NR < PQ+QR$

indication : introduire Q’ intersection de (QN) et de (PR).

– Résolution pour un triangle ABC où les angles sont inférieurs à 120°.

Étant donné un point M du plan, le problème est de minimiser la distance $MA+MB+MC$. D’où l’idée de travailler sur la fonction
$f : P \rightarrow R$, $M \mapsto MA+MB+MC$.

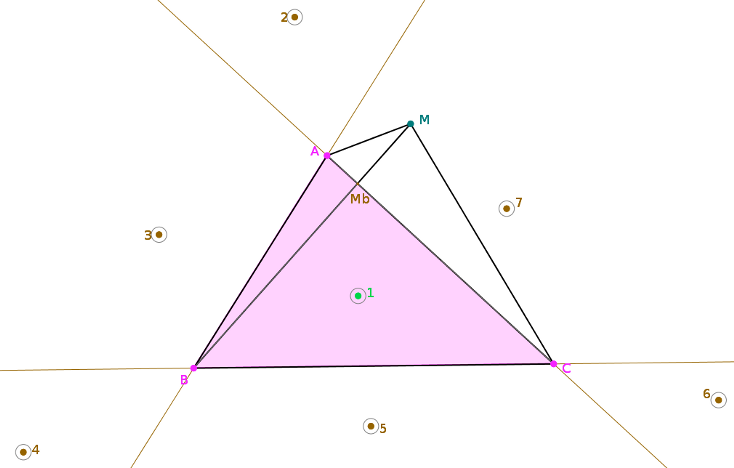
Le triangle des 3 villes délimite 7 zones du plan.
Montrer que :
– si M en 2, $f(M)$ a un minimum atteint en A
– si M en 3, $f(M)$ a un minimum atteint en I où $ \{ I \}=(MC) \cap (AB) $
– Régions 4, 5, 6, 7 ?
– si M en 1, Toricelli a démontré en 1659 qu’il existe un point T intérieur au triangle qui rend $f(M)$ minimum.

La figure CarMetal qui suit permet de rechercher le ou les minimums éventuels de $MA+MB+MC$.

<carmetals|doc=4424|largeur=800|hauteur=600>

Il faut d’abord initialiser le point Min en bougeant le point initMin, puis en déplaçant le point M, la distance s’affiche et le point Min se déplace. On peut ainsi chercher de proche en proche la position du point M qui rend cette distance minimale.

Le bouton "Solution" vous affichera la solution géométrique et le calcul associé. La construction du point solution, appelé point de Fermat, ou point de Toricelli, est celle donnée dans Wikipédia sur cette page.

Recherche de la distance minimum $MA+MB+MC$ : le point de vue analytique (algébrique ?)

La fonction $f : P \mapsto R$ qui à $M$ associe le réel positif $MA+MB+MC$ donne dans un repère du plan une fonction où interviennent deux variables : l’abscisse et l’ordonnée du point M. La recherche du minimum de f revient donc à une recherche de minimum pour une fonction de 2 variables, et ça, nous ne savons pas le faire en première S.

Par contre, ce problème peut se ramener à une recherche algorithmique de minimum puisque la fenêtre de CarMetal est un rectangle de l’écran contenant un certain nombre de pixels en abscisse et en ordonnée. En balayant de manière systématique la fenêtre de tracé de CarMetal pour le point M, on peut calculer la distance $MA+MB+MC$ pour tous les points de l’écran et en chercher le minimum.

Le code qui permet de calculer $f(M)$ dans le repère de CarMetal est :

xM=X("M"); yM=Y("M"); // on récupère les coordonnées des points dont nous avons besoin
xA=X("A"); yA=Y("A");
xB=X("B"); yB=Y("B");
xC=X("C"); yC=Y("C");

distance=Math.sqrt((xM-xA)*(xM-xA)+(yM-yA)*(yM-yA))+Math.sqrt((xM-xB)*(xM-xB)+(yM-yB)*(yM-yB))+Math.sqrt((xM-xC)*(xM-xC)+(yM-yC)*(yM-yC)); // calcul de f(M)
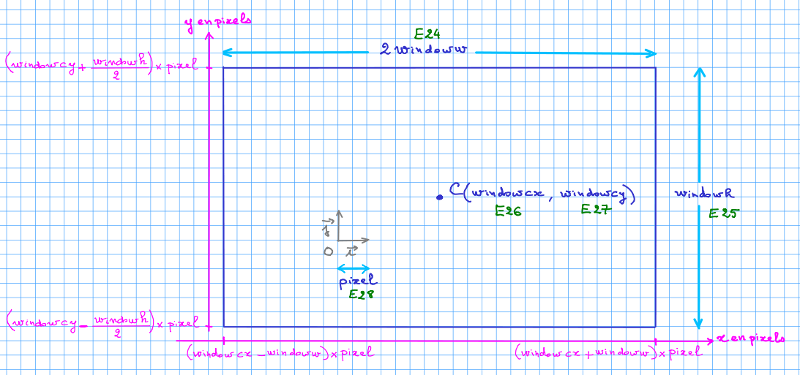
Println("MA+MB+MC = "+distance); // affichage de f(M)

Dans le repère orthonormé $R$ de CarMetal $(O, \vec{i}, \vec{j})$, la fenêtre de géométrie a les caractéristiques suivantes, en unités CarMetal données par le repère $R$ :
– sa demi-largeur : windoww
– sa longueur : windowh
– les coordonnées de son centre C : $C$(windowcx, windowcy)
– le nombre de pixels compris dans une unité du repère est pixel.

Les coordonnées en pixels de la fenêtre sont donc données par le schéma suivant :

En créant des expressions qui contiennent ces valeurs, nous pouvons les transmettre au carscript :

ExpressionsAutoroutesDeFermat

Les expressions associées sont indiquées sur le schéma de la fenêtre CarMetal et le code qui en résulte est celui-ci :

windoww=GetExpressionValue("E24");
windowh=GetExpressionValue("E25");
windowcx=GetExpressionValue("E26");
windowcy=GetExpressionValue("E27");
pixel=GetExpressionValue("E28");

Pour balayer la fenêtre et parcourir tous les points M de cette fenêtre, il nous faut une double boucle for : une première boucle balaye les abscisses en pixels de wlDebut à wlFin avec :

wlDebut=(windowcx-windoww)*pixel;
wlFin=(windowcx+windoww)*pixel;

et une seconde balaye les ordonnées en pixels de whDebut à whFin avec :

whDebut=(windowcy-windowh/2)*pixel;
whFin=(windowcy+windowh/2)*pixel;

La double boucle se code alors ainsi :

min=1000; //on initialise le minimum à une valeur assez grande

for (wl=wlDebut; wl<wlFin; wl=wl+1){
	for (wh=whDebut; wh<whFin; wh=wh+1){
		xM=wl/pixel; //wl et wh étant en pixels, on revient aux unités du repère de CarMetal
		yM=wh/pixel;
		distance=Math.sqrt((xM-xA)*(xM-xA)+(yM-yA)*(yM-yA))+Math.sqrt((xM-xB)*(xM-xB)+(yM-yB)*(yM-yB))+Math.sqrt((xM-xC)*(xM-xC)+(yM-yC)*(yM-yC));
		if (distance<min){
			min=distance;
			xMFermat=xM; // on stocke les coordonnées du point qui réalise le minimum
			yMFermat=yM;
		}
	}
}

Il ne reste plus qu’à afficher, à la sortie de la double boucle, les valeurs contenues dans les variables min, xMFermat et yMFermat. Il en résulte le carscript suivant :

**Script de recherche de la distance minimale**

Comme c’est magique, l’exécution du carscript nous fournit une valeur approchée de la distance minimale à $10^{-5}$ près.

Si $l$ est l’indice qui va balayer la largeur de la fenêtre et $h$ est celui qui va balayer la hauteur de la fenêtre, l’algorithme utilisé se résume à :

Entrer $x_A, y_A, x_B, y_B, x_C, y_C $
Entrer $lDebut, lFin, hDebut, hFin $
$ min \leftarrow 1000 $
$ x_M \leftarrow 0 $
$ y_M \leftarrow 0 $
$ x_{Fermat} \leftarrow 0 $
$ y_{Fermat} \leftarrow 0 $
Pour $l$ allant de $lDebut$ à $lFin$
Pour $h$ allant de $hDebut$ à $hFin$
$ x_M \leftarrow \frac{ l}{ pixel } $
$ y_M \leftarrow \frac{ h}{ pixel } $
$ f(M) \leftarrow \sqrt{(x_M-x_A)^2 + (y_M-y_A)^2} + \sqrt{(x_M-x_B)^2 + (y_M-y_B)^2} + \sqrt{(x_M-x_C)^2 + (y_M-y_C)^2}$
Si $ f(M) < min $ Alors
$ min \leftarrow f(M) $
$ x_{Fermat} \leftarrow x_M $
$ y_{Fermat} \leftarrow y_M $
FinSi
FinPour
FinPour
Afficher $min, x_{Fermat}, y_{Fermat}$

Exercice : En téléchargeant le fichier AutoroutesDeFermat.zirs, seule la première figure contient le carscript décrit ici, je vous propose de transporter ce script dans la 2e figure.

Recherche de la distance minimum $MA+MB+MC$ : c’est possible aussi à la calculatrice TI-82 !

La fenêtre de la TI-82 a pour dimensions 96 pixels de large et 64 pixels de haut. En laissant 1 pixel pour le cadre de chaque côté, la largeur va donc compter 94 pixels à balayer et la hauteur 62 pixels, comme le montre le schéma suivant :

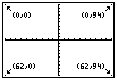
La fenêtre graphique paramétrée dans "Window" (ou "fenêtre") a des variables dont nous avons besoin : $Xmin$, $Xmax$, $Ymin$, $Ymax$. $Xmax-Xmin$ représente les abscisses parcourues pour 94 pixels de large, et $Ymax-Ymin$, les ordonnées parcourues pour 62 pixels de haut.

L’algorithme à implémenter sur la TI-82 devient alors :

Entrer $x_A, y_A, x_B, y_B, x_C, y_C $
$ min \leftarrow 1000 $
Pour $l$ allant de 0 à 94
Pour $h$ allant de 0 à 62
$ x_M \leftarrow Xmin + l*\frac{Xmax-Xmin}{ 94 } $
$ y_M \leftarrow Ymax - h*\frac{Ymax-Ymin}{ 62 } $
$ f(M) \leftarrow \sqrt{(x_M-x_A)^2 + (y_M-y_A)^2} + \sqrt{(x_M-x_B)^2 + (y_M-y_B)^2} + \sqrt{(x_M-x_C)^2 + (y_M-y_C)^2}$
Si $ f(M) < min $ Alors
$ min \leftarrow f(M) $
$ x_{Fermat} \leftarrow x_M $
$ y_{Fermat} \leftarrow y_M $
FinSi
FinPour
FinPour
Afficher $min, x_{Fermat}, y_{Fermat}$

Cet algorithme une fois implémenté sur la TI-82 donne, après avoir testé le source si vous le souhaitez, à l’aide du TI-Editor :

Si vous avez le câble de connexion TI-82, vous pouvez charger directement ce fichier binaire , sinon, voici le code source à copier-coller :

Prompt A,B,C,D,E,F
1000→M
For(L,0,94)
For(H,0,62)
Xmin+L*(Xmax-Xmin)/94→X
Ymax-H*(Ymax-Ymin)/62→Y
√((X-A)^2+(Y-B)^2)+√((X-C)^2+(Y-D)^2)+√((X-E)^2+(Y-F)^2)→Z
If Z<M
Then
Z→M
X→P
Y→Q
End
End
End
Disp M
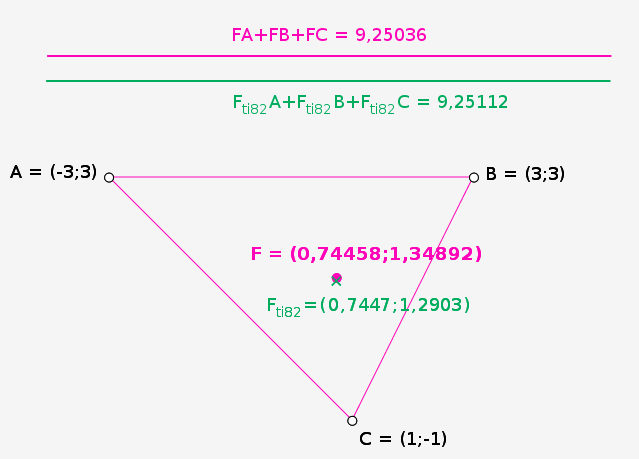
Disp P,Q

L’exécution du programme donne finalement pour $A(-3 ; 3)$ $B(3 ; 3)$ et $C(1 ; -1)$ les valeurs approchées suivantes :
$ min = 9.25112 $
$ x_{Fermat} = 0.7447 $
$ y_{Fermat} = 1.2903 $
J’ai utilisé CarMetal et la macro-construction « Point de Fermat » pour voir que finalement, le calcul effectué avec la calculatrice est tout à fait acceptable :

Recherche de la distance minimum $MA+MB+MC$ avec Scratch

– La fenêtre de Scratch

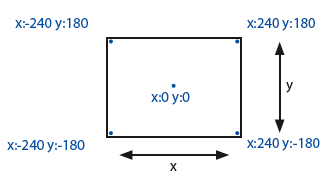
Nous allons directement travailler avec des coordonnées en pixels. L’algorithme à implémenter sur Scratch devient alors :

Entrer $x_A, y_A, x_B, y_B, x_C, y_C $
$ min \leftarrow 1000 $
Pour $l$ allant de -240 à 240
Pour $h$ allant de -180 à 180
$ x_M \leftarrow l $
$ y_M \leftarrow h $
$ f(M) \leftarrow \sqrt{(x_M-x_A)^2 + (y_M-y_A)^2} + \sqrt{(x_M-x_B)^2 + (y_M-y_B)^2} + \sqrt{(x_M-x_C)^2 + (y_M-y_C)^2}$
Si $ f(M) < min $ Alors
$ min \leftarrow f(M) $
$ x_{Fermat} \leftarrow x_M $
$ y_{Fermat} \leftarrow y_M $
FinSi
FinPour
FinPour
Afficher $min, x_{Fermat}, y_{Fermat}$

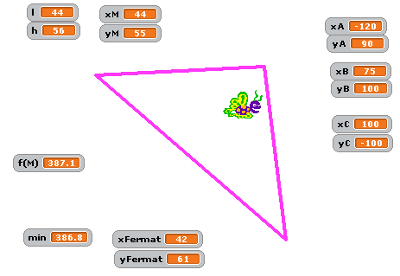
L’exécution du programme donne finalement pour $A(-120 ; 90)$ $B(75 ; 100)$ et $C(100 ; -100)$ les valeurs approchées suivantes (vous pouvez le lancer avant d’aller dormir... [3]) :
$ min = 386.8 $
$ x_{Fermat} = 42 $
$ y_{Fermat} = 61 $

Ce qui est intéressant avec Scratch, c’est de voir l’abeille se déplacer à largeur en pixel fixe, le long de la hauteur de la fenêtre, et de regarder comment le calcul du minimum se fait.