1 2 3 4 5 6 7 8

Algèbre

L’ensemble des expressions algébriques est aussi un langage.

Par exemple, une règle de ce langage est que le nombre de parenthèses ouvrantes doit être égal au nombre de parenthèses fermantes.

Puisqu’une expression est un mot d’un langage, on peut utiliser un arbre syntaxique (utile pour l’algorithmique des compilateurs) pour la représenter. Par exemple l’expression $(2x+1)(x-2)$ s’analyse successivement comme ceci :

• Un produit ;
  • Le premier facteur est une somme ;
    • Le premier terme du premier facteur est un produit, de $2$ par $x$ ;
    • Le deuxième terme du premier facteur est $1$ ;
  • Le second facteur est une différence ;
    • Son premier terme est $x$ ;
    • Son deuxième terme est $2$.

Cette description, inspirée par les grammaires transformationnelles, est en fait la représentation d’un arbre, que voici :

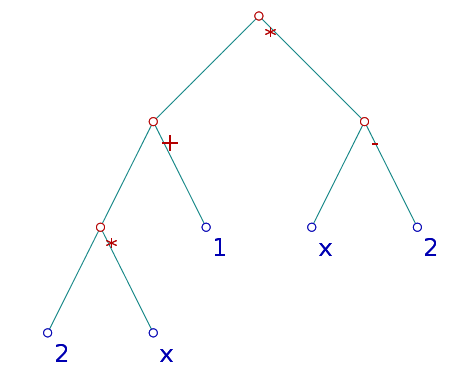
C’est en lisant l’arbre de gauche à droite qu’on retrouve $(2x+1)(x-2)$ (les parenthèses représentent les sous-arbres). Mais on peut aussi lire l’arbre de haut en bas, ce qui donne la notation polonaise pour l’expression algébrique : $*+*2x1-x2$ qui ne nécessite pas de parenthèses (elle n’est pas ambigüe).

Lorsqu’on ajoute l’existence pour tout mot non vide, d’un inverse pour la concaténation, on transforme le monoïde en un groupe, et tout groupe peut être décrit comme un langage de ce genre ; on parle alors de présentation par générateurs (les éléments de $V$) et relations (les axiomes du langage).

Par exemple, le complémentaire du noeud de huit (qui est un espace hyperbolique de dimension 3)

a pour groupe fondamental celui engendré par les trois matrices

$$a=\frac{1}{2}\left(\begin{array}{rr}3+i\sqrt{3}& -1-i\sqrt{3}\\1+i\sqrt{3}&1-i\sqrt{3} \end{array}\right)$$

$$b=\frac{1}{2}\left(\begin{array}{rr}1-i\sqrt{3}& 1+i\sqrt{3}\\-2&2 \end{array}\right)$$

$$c=\frac{1}{2}\left(\begin{array}{rr}1& 1+i\sqrt{3}\\0&2 \end{array}\right)$$

qui vérifient les relations $ab^{-1}cb=\left(\begin{array}{rr}1&0\\0&1\end{array}\right)$ et $abc^{-1}a^{-1}c=\left(\begin{array}{rr}1&0\\0&1\end{array}\right)$. Ces deux relations décrivent le groupe de façon univoque, et elles peuvent s’interpréter comme des règles de réécriture :

$$b^{-1}cb\rightarrow a$$

$$c^{-1}ac\rightarrow ab$$

1 2 3 4 5 6 7 8