Suites
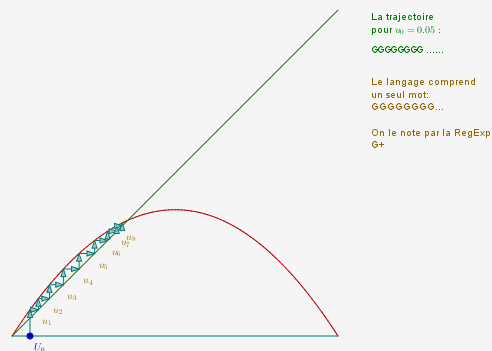
Des mots infinis peuvent apparaître dans l’étude de suites itérées comme $u_{n+1}=k u_n (1-u_n)$, en utilisant le codage suivant :
- Chaque fois que $u_k<\frac{1}{2}$, la k-ième lettre du mot sera "G" (initiale du mot "gauche" ;
- Chaque fois que $u_k>\frac{1}{2}$, la k-ième lettre du mot sera "D" (initiale de "droite".
On peut convenir que lorsqu’il n’y a que des "G" à partir d’un certain rang, on n’en écrit qu’un, et le mot est alors fini comme dans les autres onglets.
Le mot associé à une suite $u_n$ dépend de son terme initial $u_0$ mais pour $k<2$, le langage ne contient qu’un seul mot et celui-ci ne dépend pas de $u_0$ (on peut modifier $u_0$ en bougeant à la souris le point bleu sur l’axe des abscisses) :
En modifiant $k$ dans la figure ci-dessus, on constate que chaque fois que quelque chose d’intéressant se passe (une "bifurcation") du point de vue topologique, un changement du langage se produit également (avec $k=2$ par exemple). L’étude de ces langages infinis s’appelle la dynamique symbolique et elle est foisonnante. Par exemple pour $k=4$ :
- L’ensemble des valeurs de $u_0$ dont le mot commence par GGD par exemple, est l’ensemble des $u_0$ tels que
$$u_1<\frac{1}{2}$$
$$u_2<\frac{1}{2}$$
$$u_3>\frac{1}{2}$$
C’est un intervalle, il est inclus dans l’ensemble des $u_0$ dont le mot commence par GG.
- Ces intervalles sont emboîtés, et leur intersection est le singleton $\left\{u_0\right\}$ : À chaque mot infini écrit dans le vocabulaire $V=\left\{ G, D \right\}$ correspond un unique $u_0 \in \left[ 0 ; 1 \right]$ : On a une bijection entre $\left[ 0 ; 1 \right]$ et $V$.
- On peut munir $V$ d’une ultradistance telle que cette bijection soit continue : C’est un homéomorphisme (noté $\varphi$ ci-dessous).
- Ce diagramme commute :
$$\begin{array}{rrcll}&& 4x(1-x) &&\\ &[0 ;1] & \hookrightarrow &[0 ;1] & \\ \varphi & \downarrow && \downarrow \varphi \\ & V^* & \hookrightarrow & V^*& \\ && s &&\end{array}$$
c’est-à-dire que $4x(1-x)=\varphi^{-1}\left( s\left( \varphi(x) \right) \right)$ : Les fonctions $s$ et $x \mapsto kx(1-x)$ sont conjuguées. Ce qui veut dire encore que tout ce qui se passe du point de vue de $V^*$ avec $s$ correspond à ce qui se passe du point de vue de $[0 ;1]$ avec $x\mapsto 4x(1-x)$.
- Or la fonction $s$ qui est conjuguée à $x\mapsto 4x(1-x)$ est extrêmement simple à "calculer" : C’est celle qui consiste à enlever la première lettre du mot (par exemple $s(GGDGDGDDG...)=GDGDGDDG...$).
La dynamique symbolique permet alors presque immédiatement de démontrer certaines propriétés de la suite $u_n$ en utilisant la fonction $s$ (première lettre du mot anglais "shift", parce qu’en enlevant la première lettre d’un mot infini, on décale les autres lettres vers la gauche). Par exemple l’existence de points périodiques pour toutes les périodes, le dénombrement des périodes, l’aspect chaotique de la suite logistique $u_n$ ...
Dans le même ordre d’idées, c’est en regardant le mot $GGDGGDGGDGGD...=(GGD)^*$ qu’on démontre l’existence pour $k>3,83$, d’une "3-période" c’est-à-dire de trois réels $a$, $b$ et $c$ tels que $4a(1-a)=b$, $4b(1-b)=c$ et $4c(1-c)=a$. C’est aussi avec la dynamique symbolique qu’on démontre le théorème de Sarkovskii.



Commentaires