Deux questions se posent alors :
- Est-on certain qu’il finira par gagner, ce pauvre robot ?
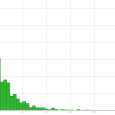
- Combien de temps la partie durera-t-elle ?
Avant le TP, l’animation en bas de page (lancer le script « jeu » ; on peut annuler les effets et recommencer autant de fois que l’on veut) a été projetée aux élèves, qui se sont immédiatement passionnés pour le sort de ce robot (par « chance », une des parties a été assez longue). Des explications ont été données sur
- le tétraèdre, forme peu connue des élèves (la plupart ne savait pas combien de faces le dé possède), et des questions intéressantes ont été posées sur la lecture du résultat du lancer, le dé n’ayant pas de face de dessus ;
- Le « switch..case » de JavaScript qui simplifie l’écriture du code (même avec seulement 4 faces) ;
- les tableaux de JavaScript, sous la forme du corrigé d’un exercice sur les diagrammes en bâtons.
- La définition du disque et le rappel des TPs sur les distances.
L’objet de ce TP est juste d’introduire l’autre sorte de boucle à condition de sortie :
- La boucle $while(b)$ tourne tant que $b$ est vraie. Donc si $b$ est fausse la boucle ne tourne jamais.
- Parfois on a besoin que la boucle soit effectuée au moins une fois, même si $b$ est fausse ; c’est l’analogue des boucles $until(\neg b)$ de Pascal (langage). En JavaScript, une telle boucle se rédige $do ... while(b)$. Dans le cas présent, on est certain que la boucle sera effectuée au moins 4 fois donc la distinction entre ces deux sortes de boucle ne présente pas d’intérêt pour cet exercice.
Le sujet du TP, au format pdf, est téléchargeable ici :
Une fois encore, les élèves se sont précipités pour copier le script au clavier, sans faire suffisamment attention à la syntaxe (oubli fréquent de points-virgule) et parfois sans lire le début de l’énoncé, qui demandait la construction du cercle !
Une fois le script entré, le spectacle de ce robot tentant parfois péniblement de sortir du cercle a été visiblement captivant pour les élèves [1] :
Lo tipwin y bouz...
Lo tipwin lé là...
Là n’a ganié !
erreurs de syntaxe
- En écrivant "case3" et "case4" sans espace entre "case" et le chiffre, le robot ne se déplace que sur l’axe des abscisses (parfois pas du tout). Bien que l’erreur de syntaxe soit difficile à corriger (on ne voit pas bien l’espace manquant), la présence d’une erreur a été immédiatement perçue par l’élève.
- Le remplacement du point-virgule par un double-point est une erreur de syntaxe signalée comme telle mais difficile à détecter, même en connaissant le numéro de la ligne.



Commentaires