Quadrilatères
Aires
En rajoutant un quatrième point aléatoire $D$ tel que $\bar{D}\left(\frac{3}{2} ;\frac{7}{2}\right)$, on a un quadrilatère aléatoire. Lla distribution de fréquences des aires ressemble à ceci :
Dans le cas gaussien :
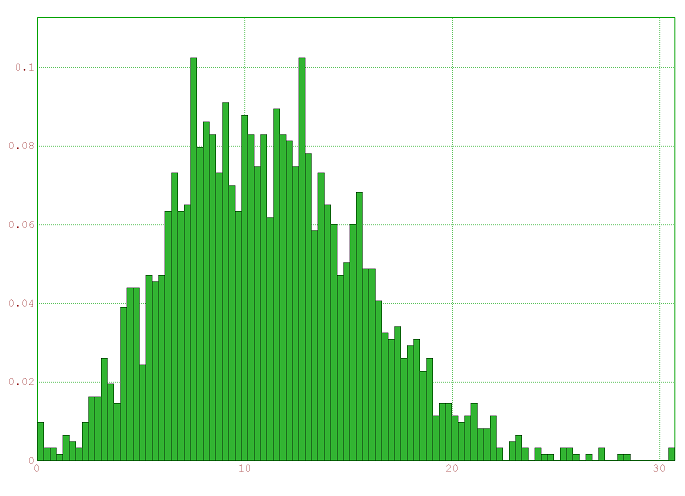
Et dans le cas uniforme :
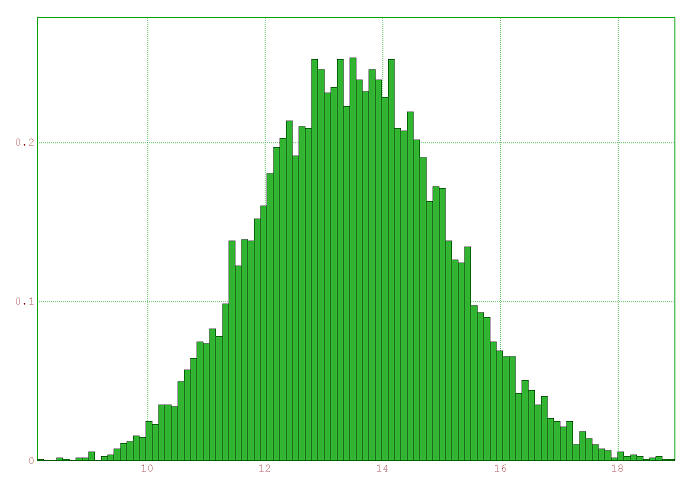
Intersection des diagonales
Sous Euler Math Toolbox, on peut facilement avoir les coordonnées du point d’intersection des diagonales $(AD)$ et $(BC)$ lineIntersection(lineThrough(A'[i],D'[i]),lineThrough(B'[i],C'[i]))'.
Dans le cas uniforme, le graphique donné par Euler Math Toolbox montre une densité pyramidale analogue à celle du milieu d’un segment aléatoire :
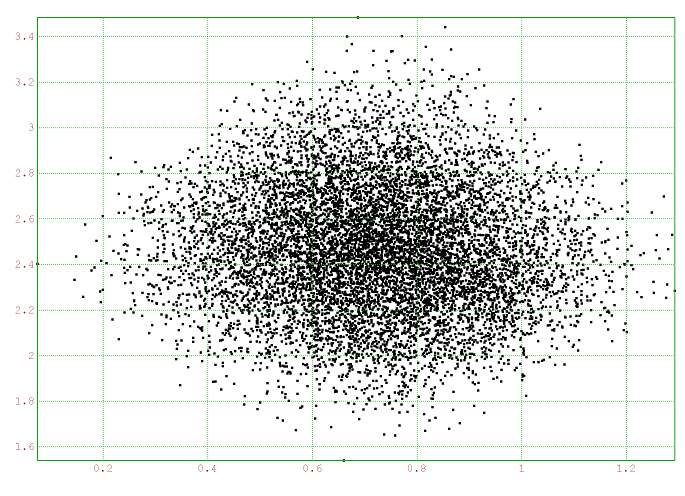
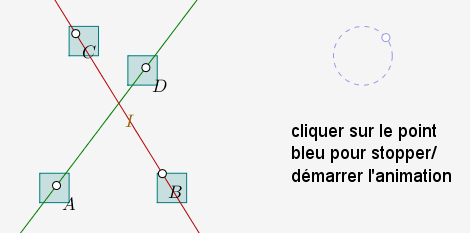
En attendant suffisamment longtemps, on peut le voir aussi sur la figure en cours de construction :
Dans le cas gaussien, le nuage est à la fois dispersé dans ses valeurs extrêmes et concentré autour de l’intersection de $(\bar{A}\bar{D})$ et de $(\bar{B}\bar{C})$ :
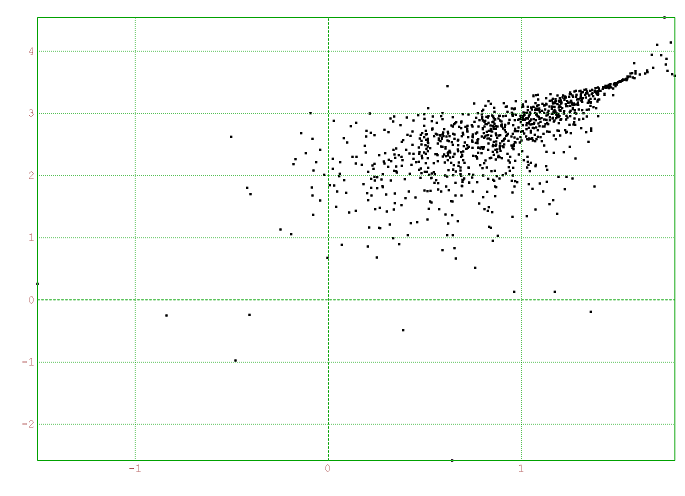
Au fait, les coordonnées du point d’intersection sont $\left(\frac{13}{18} ;\frac{133}{54}\right)$
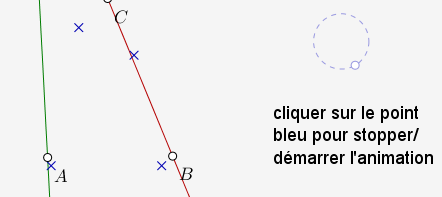
L’allure du nuage se confirme sur la figure ci-dessous, en cours de construction :
On constate en passant l’ampleur du mouvement d’une droite passant par deux points gaussiens (comparé au cas uniforme).
Cercles
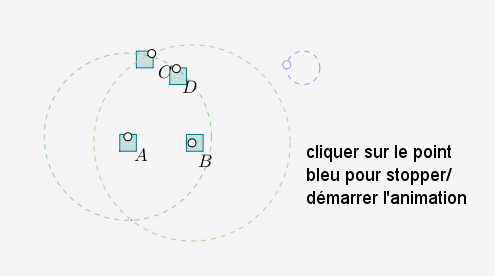
Pour finir en beauté, voici, dans le cas uniforme, le nuage des intersections du cercle de centre $A$ passant par $D$ et du cercle de centre $B$ passant par $C$ (deux nuages de points, qui semblent homothétiques) :




Commentaires