Cercle circonscrit
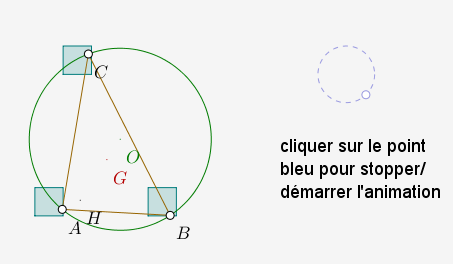
En représentant le centre du cercle circonscrit (en vert) avec l’orthocentre (en noir) et le centre de gravité (en rouge), l’alignement des trois centres ne saute pas aux yeux :
les trois centres
Par contre on voit ci-dessus que les nuages extrêmes sont homothétiques.
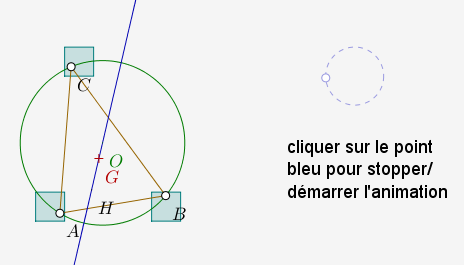
Pour vérifier l’alignement des trois centres il suffit d’ajouter la droite joignant deux d’entre eux (ci-dessous l’orthocentre et le centre du cercle circonscrit) et de vérifier visuellement qu’elle passe bien par le troisième point :
droite d’Euler
En téléchargeant le fichier "droite d’Euler" ci-dessous, on peut l’ouvrir avec CaRMetal et cocher l’onglet "trace visible" sur la droite d’Euler. Ce qui permet de voir à quoi ressemble une droite aléatoire. Le spectacle est ... indescriptible !
Commentaires