Tout jeu de Nim peut être modélisé par le déplacement d’un pion sur un graphe orienté. Mais en fait, tout jeu combinatoire peut de façon analogue être modélisé par le déplacement d’un pion sur un automate binaire, l’un des joueurs ne pouvant déplacer le pion que le long d’une flèche bleue, l’autre ne pouvant déplacer le pion que le long d’une flèche rouge. Cette construction, imaginée par John Conway dans les années 1970, comprend entre autres des nombres. Conway permet d’additionner et multiplier tous les jeux, pas seulement les nombres. Pour la semaine des maths 2023 (thème : les mathématiques à la carte) chaque jeu de Conway a été représenté sur une carte, et en considérant ces cartes comme des pays sur une carte on modélise l’addition et notamment celle des nombres.
Un exemple : alquerkonane
Le jeu alquerkonane a du succès dans toutes les classes, par exemple en CE 2 :
Pour chaque position d’alquerkonane, on joint par une flèche bleue toute position accessible aux noirs, et par une flèche rouge toute position accessible aux blancs. On obtient alors un graphe à deux couleurs (un automate binaire, la position initiale étant marquée d’une flèche et les positions finales, d’un double cercle), où le gagnant est celui qui mène le pion à une position finale :
On voit ci-dessus qu’il n’y a pas que des entiers dans alquerkonane, il n’y a même pas que des nombres. Il y a aussi des infinitésimaux, comme ici (extrait de mathématiques et jeux de société bib83 dans tangente) :
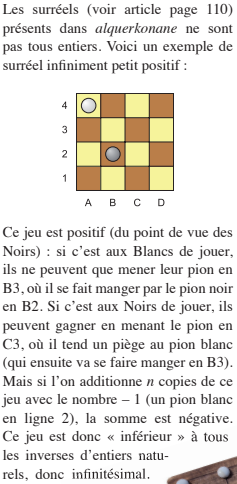
Des infinitésimaux peuvent aussi apparaître dans d’autres jeux comme les échecs ou hex :
Une carte pour un jeu
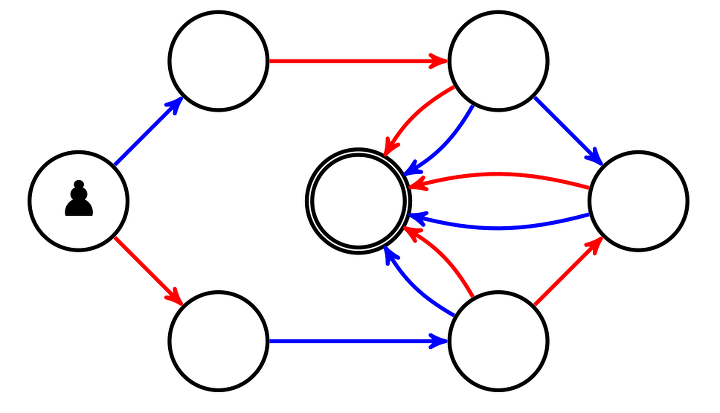
Pour inventer son propre jeu, il suffit donc de dessiner des flèches rouges et bleues entre des cercles (les sommets du graphe). Par exemple voici un jeu créé par une élève de Grande Section :
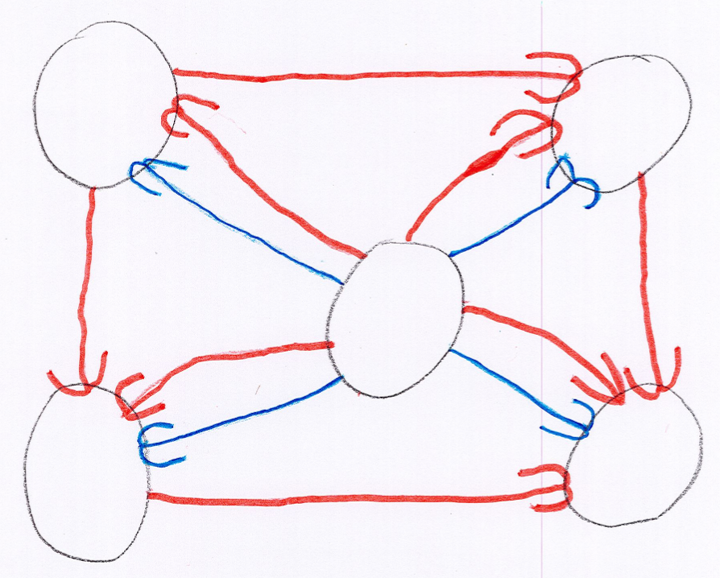
Pour jouer, il faut placer le pion sur le sommet central (le départ). Voici un exemple où les bleus gagnent en marquant le (dernier) but :
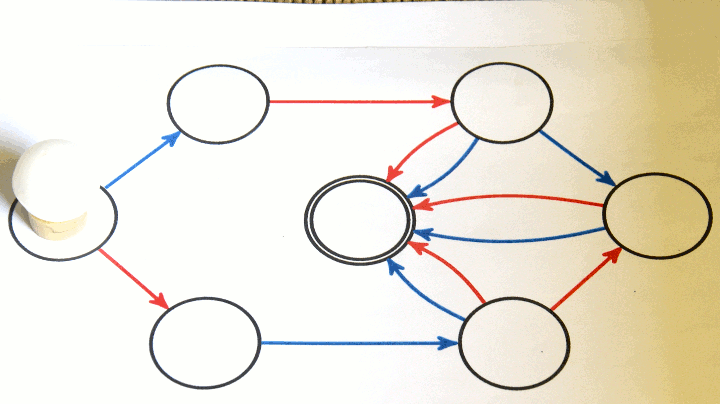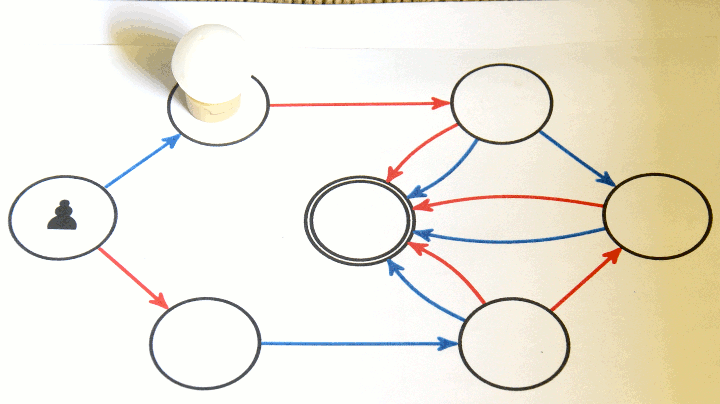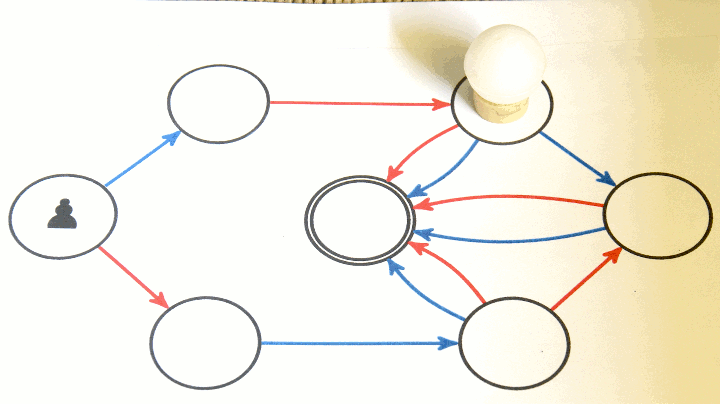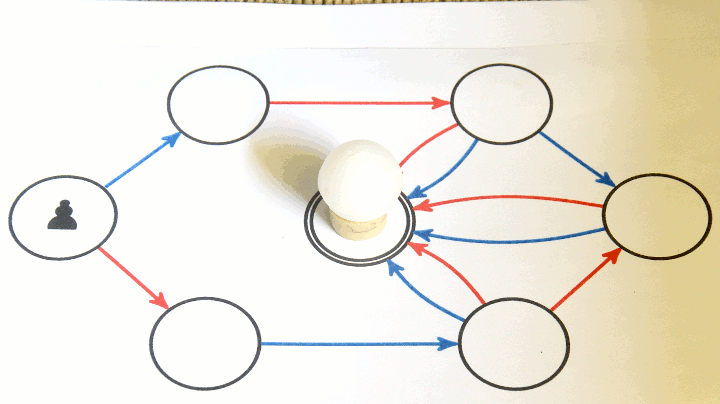
Voici quelques exemples de jeux modélisés de cette manière (théorie de Conway) :
On peut créer et tester son jeu en ligne.
L’addition des jeux par cartes juxtaposées
Pour la semaine des maths, les cartes suivantes ont été créées :
Puis un add-on pour les jeux infinitésimaux (plus intéressant car la stratégie gagnante est moins évidente) :
Et, pour les élèves daltoniens, une version en noir et blanc :
et la version noir et blanc des infinitésimaux :
Une fois les cartes posées sur la carte des cartes, pour jouer, il faut poser un pion au départ de chaque carte. Le premier qui ne peut plus bouger a perdu. Par exemple, voici un jeu inventé par un élève de CM1, avec 3 cartes :

Ce sont les rouges qui gagnent, puisqu’ils marquent le troisième but (alors même que les bleus avaient marqué les deux premiers buts).
Retour aux jeux de Nim
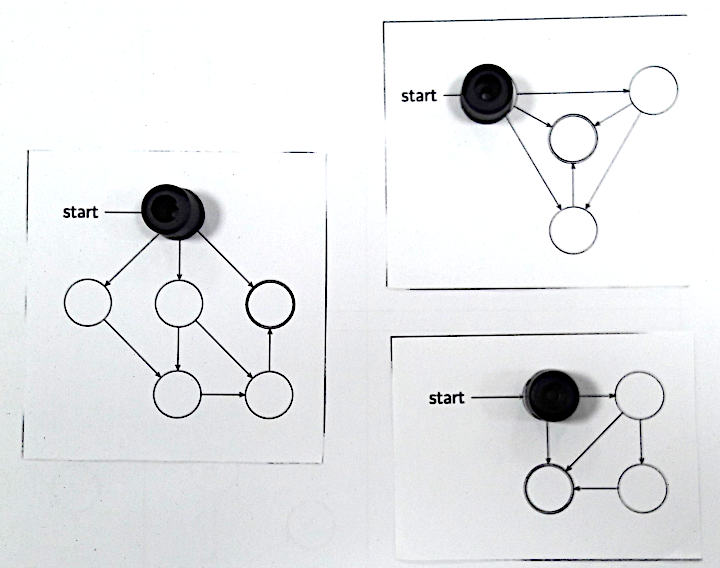
Dans le cas des jeux impartiaux, il n’y a, par définition, plus besoin de couleurs. Aviezri Fraenkel a modélisé tous les jeux impartiaux (de type Nim) par des graphes de ce genre:
Le théorème de Sprague-Grundy dit que tout jeu impartial est équivalent à l’une des cartes ci-dessus (du moins pour les petits nombres de Grundy ; sinon il faut d’autres cartes). La nouveauté de 2025, c’est que comme plus haut, on peut construire un jeu impartial en plaçant côte à côte plusieurs de ces cartes, chacune munie d’un pion, dont la position de départ est étiquetée start, et dont la position d’arrivée est le double-cercle (il n’y en a qu’un par carte). Celui qui effectue le dernier mouvement, gagne le jeu. Par exemple, ci-dessous, il y a un coup gagnant :
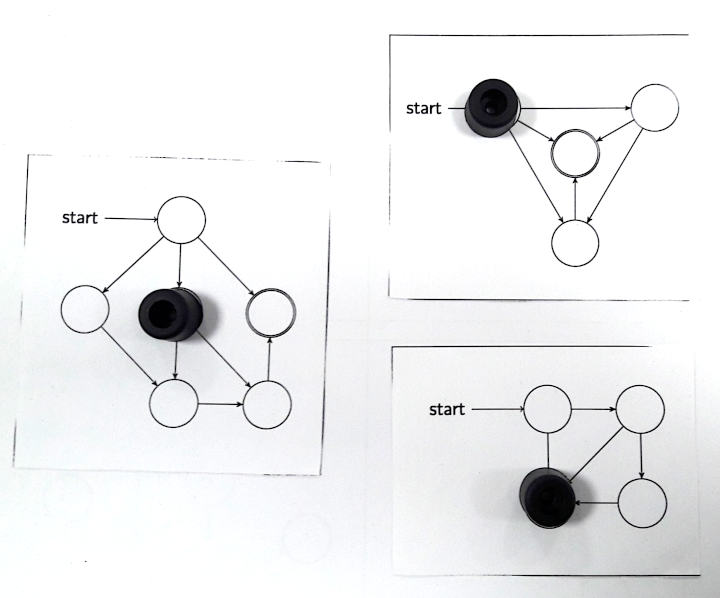
Lequel ? Pour le savoir, une astuce utile : le nombre de Grundy de la somme de ces trois cartes est la nim-somme des nombres de Grundy des trois termes (de haut en bas, 3, 2 et 0, donc le nombre de Grundy de ces trois cartes est 1…



Laisser un commentaire