Fractran

Fractran est un langage de programmation Turing-complet, ainsi que le prouve son créateur :

L’intérêt essentiel de Fractran est qu’il est basé sur les fractions. Ce langage permet donc de faire travailler à la fois

• les algorithmes
• le calcul sur les fractions
• la décomposition en facteurs premiers

Voici un exemple de programme Fractran, pour voir le principe. Et un programme de multiplication en Fractran (basé sur la décomposition en facteurs premiers).

Voici maintenant un interpréteur Fractran en Sofus :

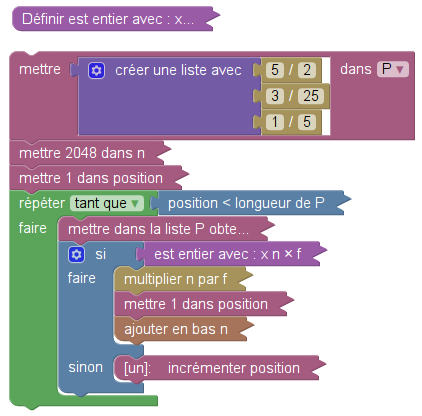
et en Python :

from fractions import *

programme = [Fraction(1,2),Fraction(2,3),Fraction(3,4),Fraction(4,5)]

def estEntier(fraction):
	return fraction.denominator == 1


def fonction(n):
    position = 0
    nombre = n	
    while position<len(programme):
        if estEntier(nombre*programme[position]):
            nombre *= programme[position]
            position = 0		
	else:
		position  += 1	
    return int(nombre)

for n in range(1,200):
    if fonction(n) == n:
        print(n,fonction(n))

(le programme Fractran a été inventé par un élève, sous forme de graphe, en SNT)

En fait, un programme Fractran est une sorte d’automate binaire, le fait que la multiplication par la fraction réussit ou échoue, conditionnant le chemin à prendre (retourner au départ en changeant de nombre, ou aller à la fraction suivante). Le programme Fractran ci-dessus (en Python) donne alors le graphe suivant :

Cela a été l’occasion d’un jeu en extérieur, coanimé par des élèves de 2nde (SNT) et des élèves de l’Alefpa, la course des fractions : chaque fraction est un point du lycée, où sont installés des élèves accueillant les concurrents, leur demandant leur nombre, vérifiant si la multiplication du nombre (du concurrent) par la fraction (de la station) réussit.

• Si la multiplication réussit, on envoie le concurrent vers le départ (en suivant la flèche bleue) où il donne au maître du jeu son nouveau nombre, et là il repart avec son nouveau nombre.
• Si la multiplication échoue, le concurrent garde son nombre actuel et est guidé vers l’étape suivante (flèche rouge).

Au départ du jeu (point d’interrogation sur le graphe), le concurrent se voit confier un nombre entier (dépendant du concurrent, ce n’est pas le même entier pour tout le monde), puis est guidé vers la première fraction. Ensuite, chaque fois qu’un concurrent arrive (en suivant une flèche bleue) au départ, il donne son nombre actuel au maître du jeu, qui vérifie si le nombre a changé depuis le dernier passage. Dans le cas contraire (le coureur est passé par une flèche rouge), il déclare que la course est finie, et note en vis-à-vis du nombre de départ, le nombre d’arrivée.

Lorsque tous les concurrents ont fini la course, on dispose d’une feuille de ce genre :

24	1
25	1
27	1
30	1
32	1
35	7
36	1
55	11
56	7
60	1

La question étant évidemment que calcule ce programme Fractran ?

On peut aussi songer à un projet où les concurrents flashent un QR-code pour géolocaliser la prochaine étape, mais dans ce cas les étapes doivent être suffisamment éloignées pour ne pas souffrir du manque de précision de la géolocalisation.

Voici un résumé de l’article de Conway, en lien avec la conjecture de Collatz :