Les programmes de calcul en cycle 3

Depuis les années 1980, Yves Chevallard propose d’entrer dans l’algèbre par le biais de programmes de calcul, et ce, dès le premier degré. On verra plus bas que les programmes de calcul peuvent être vus comme une généralisant les problèmes de changement d’état dans la classification de Gérard Vergnaud. Traditionnellement, on les présente comme des tours de magie, comme le faisait Claude Gaspard Bachet de Méziriac au début du XVII^e siècle :

Cet exemple de programme de calcul, de par son âge respectable (4 siècles au moins), servira à illustrer les outils présentés dans cet article.

Dans le programme de cycle 3 de 2025, on lit, comme objectif d’apprentissage en algèbre en CM 1 :

Exécuter un programme de calcul

et en CM 2 :

Exécuter ou produire un programme de calcul

Dans cet article, on décrit divers outils permettant d’étudier des programmes de calcul (en CM 1 et CM 2) voire d’en créer (en CM 2).

Flow974Primaire

L’outil est en ligne. On a une version à une étape (pour modéliser des changements d’état dans la classification de Vergnaud), mais pour le programme de Bachet, on a besoin de la version à 5 étapes.

Le programme de calcul par défaut est

1. ajouter 2
2. ajouter 1
3. ajouter 5
4. ajouter 3
5. ajouter 8

alors que celui de Bachet est

1. multiplier par 2 (doubler)
2. ajouter 5
3. multiplier par 5 (quintupler)
4. ajouter 10
5. multiplier par 10 (décupler)

Il faut donc cliquer sur les signes opératoires pour les remplacer (via des menus déroulants) par les bonnes opérations, et sur les opérandes pour les ajuster (par exemple avec les flèches à droite pour augmenter ou diminuer). Quand on arrive à cela :

on peut bouger le nombre à gauche (pour l’instant 8) afin d’émettre des conjectures sur ce programme de calcul.

Flow974

flow974 était plus adapté aux programmes de calcul du DNB, mais au nom du qui peut le plus, peut le moins, on peut, a minima, envisager de s’en servir en 6^e, comme transition entre les programmes de calcul flow974primaire et la programmation visuelle par blocs (voir plus bas). On peut programmer par exemple ainsi le tour de magie de Bachet :

On peut ensuite modifier le nombre de gauche (en modifier un autre ferait changer de programme de calcul) pour étudier le programme de calcul.

Tableur

Comme exemple, on choisit le plus connu des tableurs libres : Calc, qui fait partie de la suite Libre Office. Pour y mettre un programme de calcul, on commence par entrer un nombre (qui sera modifié plus tard) en A1, puis on écrit en A2 la formule =A1*2 :

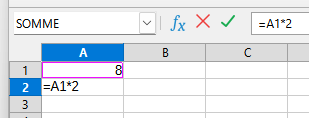
puis, en A3, la formule =A2+5 :

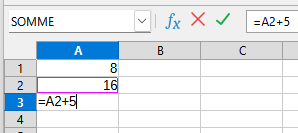
Ensuite, pour rester conforme aux instructions de Bachet, on place en A4 la formule =A3*5, puis en A5 la formule =A4+10, et en A6 la formule =A5*10. On obtient alors ce fichier :

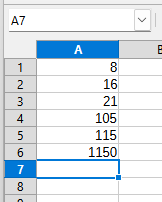
SofusColl

Sofus est un langage de programmation créé à l’origine pour programmer des programmes de calcul. La version collège est utilisable dès le CM 1 (à condition de ne faire que des programmes de calcul, avec les instructions de la partie sofus). Le programme de Bachet ressemble à ceci :

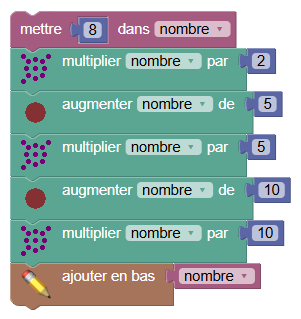
En cliquant sur le drapeau vert, on voit la valeur finale du nombre :

On peut modifier la valeur de départ et recliquer sur le drapeau vert, mais aussi, on peut mettre la lettre N comme nombre de départ :

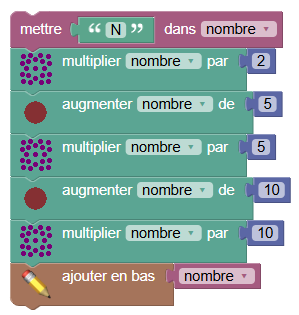
un nouveau clic sur le drapeau vert donne l’affichage suivant :

qui explique pourquoi Bachet a rajouté l’étape de soustraire 350 et ne pas regarder les deux derniers chiffres.

Pour décortiquer l’expression algébrique finale, il suffit d’ajouter des affichages à chaque étape :

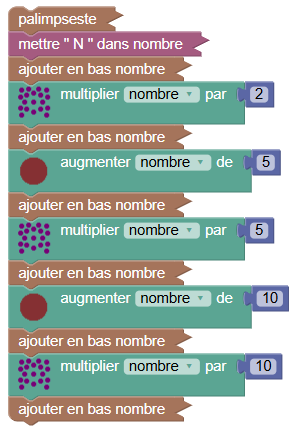
Le clic sur le drapeau vert affiche alors les valeurs littérales des expressions algébriques successives :

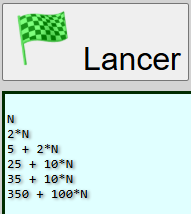
En débranché

Mais le meilleur moyen d’étudier des programmes de calcul, c’est encore avec un crayon sur du papier. Voici le programme de calcul de Bachet, à imprimer :

L’élève peut écrire un nombre de son choix dans le cercle de gauche, puis compléter le graphe.

Et avec la version sans opération, on peut même inventer son propre programme de calcul :

Noter que ces graphes peuvent aussi servir en 1^ère, pour la préparation de l’épreuve anticipée du bac, puisque dans la partie évolution et variations les compétences attendues sont

• Passer d’une formulation additive (« augmenter de 5 % », respectivement « diminuer de 5 % ») à une formulation multiplicative (« multiplier par 1,05 », respectivement « multiplier par 0,95 »).
• Appliquer un taux d’évolution pour calculer une valeur finale ou initiale.
• Calculer un taux d’évolution, l’exprimer en pourcentage.
• Calculer le taux d’évolution équivalent à plusieurs évolutions successives.
• Calculer un taux d’évolution réciproque.