Tournois de jeux mathématiques à deux joueurs

Jeux à 2 joueurs

Dans le programme de CPGE MPI, un jeu à deux joueurs se joue à l’aide d’un pion sur une arène :

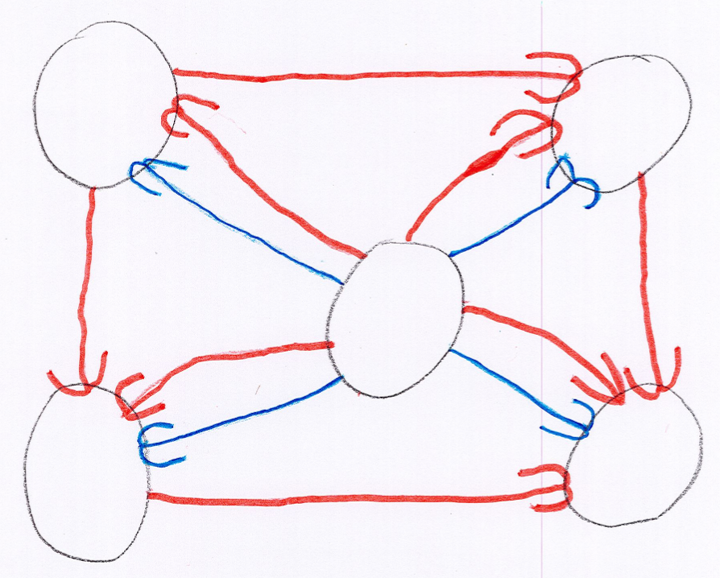
Si le pion est sur un sommet circulaire, c’est à Eve de jouer, sinon c’est à Adam de jouer (la présence d’une flèche allant d’un sommet circulaire à un sommet circulaire permettrait alors à Eve de jouer deux fois de suite). Si le pion arrive dans un sommet circulaire et final, Eve gagne et si le pion arrive dans un sommet carré et final c’est Adam qui gagne. Par exemple le jeu hexapawn, bien connu des pionniers de l’IA, a ce graphe :

(ici les flèches rouges désignent les mouvements des noirs, et les flèches bleues ceux des blancs ; avec alquerkonane ce sera le contraire). Le graphe ci-dessus est bien une arène :

Pour inventer un jeu à deux joueurs, on peut aussi utiliser la carte des cartes, voici par exemple un jeu créé par une élève de Grande Section :

et (avec plusieurs cartes) des jeux plus récents, comme celui-ci (à 5 pions) créé par une collégienne :

Pour les tournois (intra ou inter écoles), on a choisi le jeu alquerkonane. En effet, ce jeu, créé par une élève de CE 1, a les caractéristiques suivantes :

• une partie dure peu de temps (environ 5 minutes)
• il y a un moyen simple de savoir qui a gagné (le premier bloqué a perdu)
• la règle du jeu est facile à retenir
• le matériel est assez facile à se procurer ou fabriquer (damiers en papier, pions matérialisés par des graines ou des cailloux de deux couleurs)

De plus, ce jeu peut aussi être à score.

Jeux à score

Parmi les jeux combinatoires à deux joueurs, on distingue

• les jeux (comme Sowing et les jeux de Nim) où le premier qui ne peut plus bouger a perdu,
• les jeux (comme go ou chungkala) où chaque joueur a un score, et le gagnant est celui qui a le plus haut score.

Par exemple, la classification des jeux de semailles entre wari (awalé etc.) et solo (katro, m’raha wa nsto etc.) illustre bien cette séparation, les wari étant des jeux à score et les solo, des jeux où le but est de vider les graines de l’adversaire de sorte qu’il n’ait plus de graines à semer.

Dans alquerkonane, le premier qui ne peut plus bouger (parce qu’il n’a plus de pions ou que ceux-ci sont bloqués au bout) a perdu. Ce qui classe alquerkonane dans la catégorie des jeux à fin normale. Mais il se trouve qu’il y a des nombres dans alquerkonane :

Pour transformer alquerkonane en un jeu à score, on utilise l’algorithme suivant :

Le premier qui ne peut plus bouger a perdu. Il gagne alors un point, auquel on ajoute le nombre de fois qu’il aurait encore pu bouger si c’était à son tour de jouer.

Les tournois ont été faits sur ce damier :

Tournoi 2023 d’alquerkonane

Avant le tournoi, les élèves ont été formés au jeu mais aussi à la notion de transfert de points entre joueurs d’une même poule, à l’aide de ce document :

Lorsqu’une partie (dans une poule) est finie, il y a forcément un gagnant et un perdant. On compte le nombre de fois que le gagnant pouvait encore bouger un de ses points, on rajoute 1 (parce que c’est le gagnant, même s’il ne pouvait plus bouger) et on obtient un nombre entier. On ajoute ce nombre au score du gagnant, et on le soustrait au score du perdant. Dans une poule de 4 joueurs, chaque joueur a augmenté (ou diminué) son score 3 fois (une fois pour chacun de ses adversaires dans la poule). On a utilisé des graphes à compléter (une flèche à ajouter et un entier à transférer), comme ceci :

Après chacun des 6 matchs de la poule, on dessine une flèche allant du perdant vers le gagnant, et on écrit le nombre de points transférés, comme ceci :

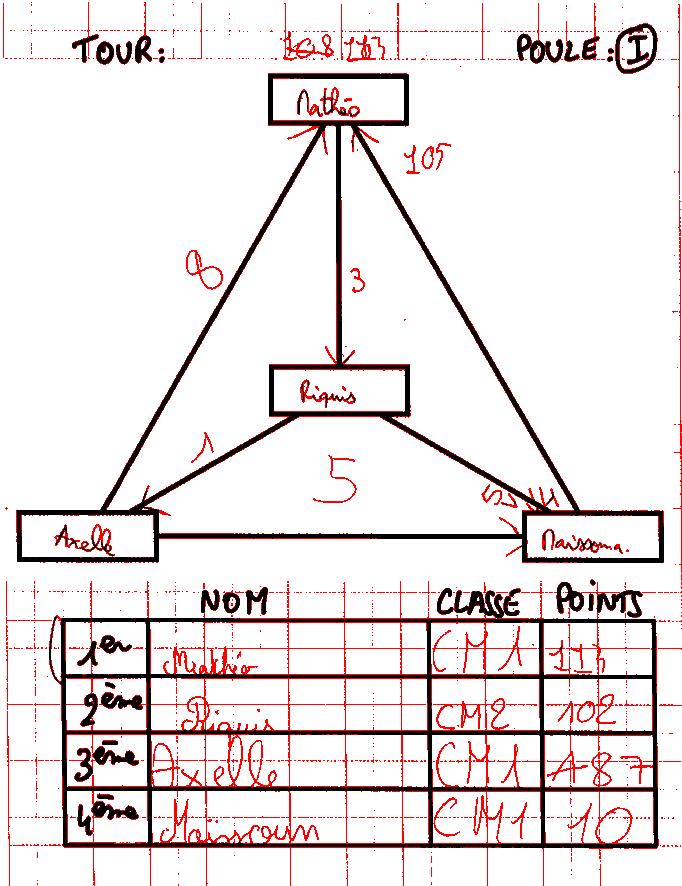
On voit ci-dessus que Mathéo a perdu contre Riquis (la flèche va de Mathéo à Riquis) de 3 points. Le score de Mathéo baisse donc de 3 points alors que celui de Riquis augmente de 3 points.

Si, au début, chaque joueur dispose d’un capital de 100 points (pour éviter de parler de nombres négatifs en CE 2), alors le nombre initial de points dans une poule de 4 est 400. Mais comme les scores n’ont évolué que par transfert de points, le score total doit aussi être 400 à la fin. Ceci permet de vérifier les erreurs de calcul comme par exemple ici :

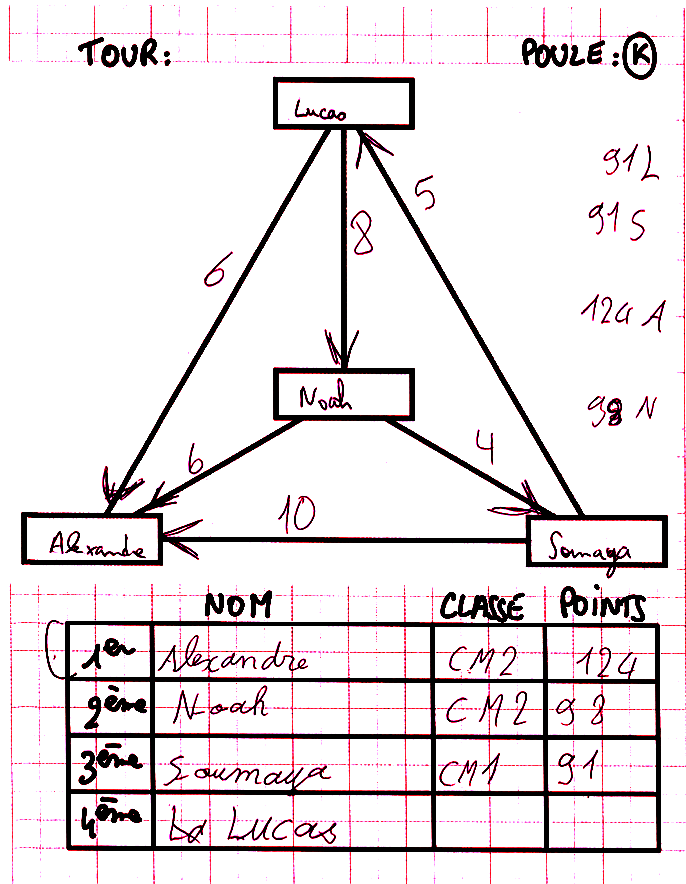
On constate qu’au bilan la somme des scores est 91+91+124+98=404 et non 400. On peut vérifier que le score d’Alexandre a été mal calculé, en étudiant son évolution au cours du temps :

On peut d’ailleurs, en lieu et place des graphes à compléter, donner directement de telles feuilles aux joueurs (ici, avec un score initial de 40 pour simplifier les calculs : des élèves de CP participaient aussi) :

On leur a préféré des tableaux de ce genre :

Voici par exemple le résultat d’une des dernières poules ayant joué le tournoi de CE 2 :

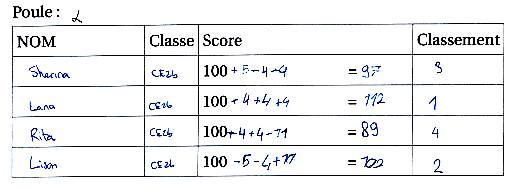
On lit par exemple que Sherina a gagné 5 points contre Lison au début, et qu’en même temps Lana a gagné 4 points contre Rita (pour Rita c’est 100-4+4-11). Avant le vrai tournoi, ces dispositifs ont été expérimentés à petite échelle dans des classes, puis en grand à la cantine de l’école Aristide Briand du Tampon (6 classes en deux sessions) :

Lors du premier round, on a constitué autant de poules de 4 que possible (en complétant par des poules de 3), puis après 6 parties on a reconstitué de nouvelles poules, par classement dans la poule précédente. Par exemple une poule du deuxième round du tournoi est formée de 4 joueurs qui avaient tous été classés 3^e de poule dans le round précédent. Pour le 2^e round on a réinitialisé tous les scores à 100. A l’issue des deux rounds, et hormis les poules de 3, chaque joueur avait joué 6 parties, et il y avait une vingtaine de premiers de poules, dont les 16 meilleurs ont été sélectionnés pour le huitième de finale.

Introduction aux cryptomonnaies

Le fait que la somme des scores est toujours 400, n’est pas vrai qu’au début et à la fin, mais après chacune des 6 parties jouées :

Chaque fois que la somme 400 est recalculée, on obtient une ligne que l’on appelle bloc, et la séquence des blocs dans une poule est une chaîne de blocs :

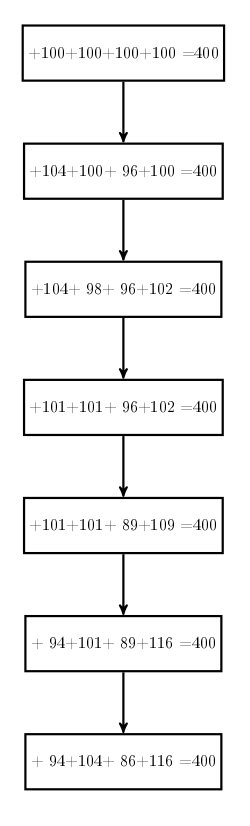
Si on constate à la fin que la somme des points n’est pas 400, c’est qu’il y a eu au moins une erreur de calcul quelque part. Où ? Pour le savoir, on fait des hypothèses, selon quel score a été introduit quand. Ceci mène à un arbre :

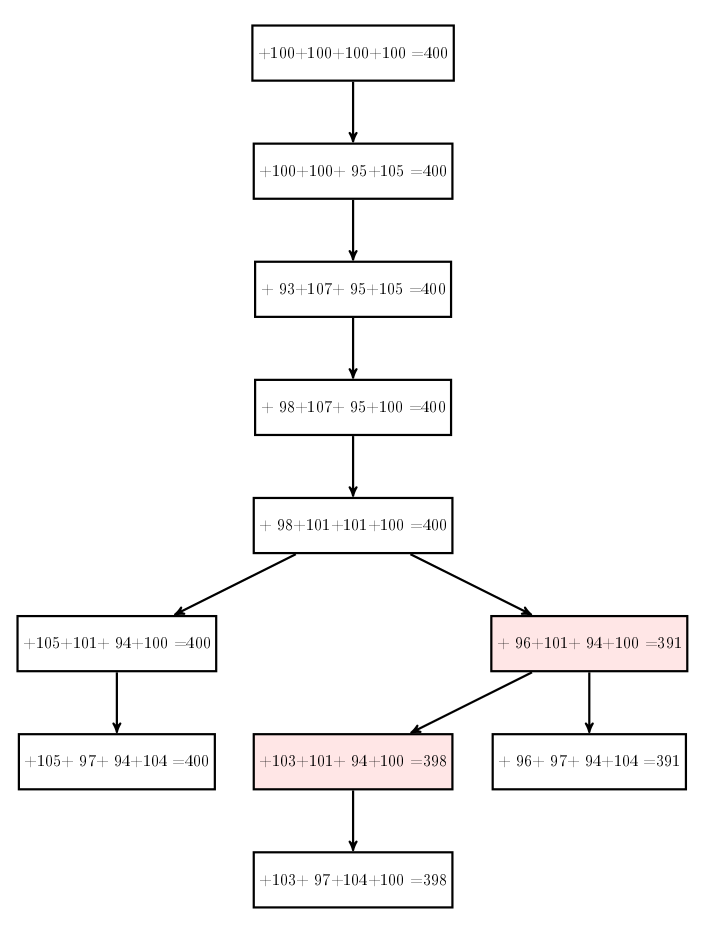
On doit alors choisir collectivement quel est le score à corriger, ce qui revient à recréer une chaîne de blocs à partir de cet arbre :

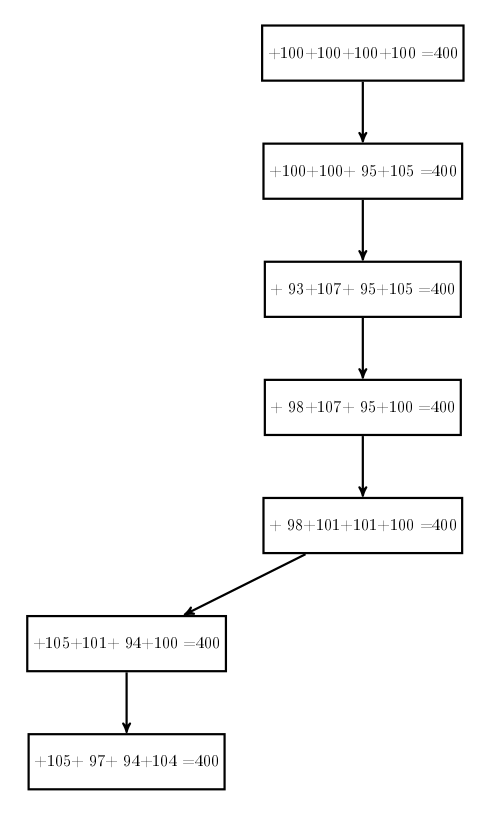
Cette validation collective des transactions (de scores) est emblématique des cryptomonnaies. Pour pousser un peu plus loin cette analogie, on peut occuper les élèves non finalistes en leur permettant de miner de la cryptomonnaie (gagner des points de repêchage), ce qui se fait en résolvant des problèmes, comme ceux-ci:

Tournoi d’alquerkonane de 2024

Pour le tournoi de la semaine des maths 2024 (thème : l’essentiel est de participer), le public s’est élargi puisqu’en plus des 6 classes de l’école Aristide-Briand, il y a eu 4 classes de l’école Jules-Ferry. Des difficultés logistiques ont empêché que le tournoi puisse se faire entre les 10 classes, il a donc fallu séparer le tournoi en 3 parties (le thème de la semaine des maths aurait dû être l’essentiel est d’essayer de participer !). Les huitièmes de finalistes ont à nouveau été sélectionnés par des classements de poules mais cette fois-ci on n’a pas calculé de scores. Les fiches de poules portaient juste des 0 ou des 1 :

Pour savoir qui joue les noirs (et commence) on joue à chifoumi. Après avoir rempli la feuille (6 parties jouées) chaque joueur totalise ses points (sur sa ligne). Il y a alors 4 cas :

• le joueur a perdu contre chacun des 3 adversaires de sa poule. Il a alors 0+0+0=0 point,
• le joueur a gagné une fois et perdu deux fois, il a alors 1+0+0=1 point,
• le joueur a perdu une fois et gagné les deux autres fois, il a alors 1+1+0=2 points,
• le joueur n’a perdu contre aucun des adversaires de sa poule, il a alors 1+1+1=3 points.

Dans le 2^e round, ont été groupés dans les poules des élèves ayant eu le même nombre de points (ou presque) au premier round. L’avantage essentiel de cette manière de faire est qu’elle s’applique à des jeux à fin normale et pas seulement à des jeux à score. Son inconvénient essentiel est la forte proportion d’ex aequo comme le cas 3+1+1+1 (dans ce cas il faut refaire jouer les ex aequo pour les départager). Comme en 2023, les 16 les mieux classés après les rounds de poule ont été huitième de finalistes. Pour chacun des tournois, le gagnant a reçu comme prix un exemplaire de ce livret d’André Dandouau sur le katro :

Après ces tournois, il y a eu une forte demande des élèves pour qu’on reprogramme un tournoi en 2025.

Le tournoi d’alquerkonane de 2025

La collecte des données de poule étant chronophage, et afin de permettre à tous les joueurs de jouer jusqu’au bout, on a expérimenté le système suisse. Le principe est de mélanger les listes d’élèves (qu’il fallait fournir avant l’organisation du tournoi proprement dit) de manière que les gagnants jouent contre les gagnants :

La distribution des nombres de points montre clairement qu’il y a eu un bug : il y a eu 3 élèves qui ont gagné 7 fois, ce que la méthode suisse ne permet pas. Une fois de plus, les problèmes logistiques ont empêché la tenue du tournoi (250 élèves prévus et le tournoi s’est déroulé en trois fois, tout d’abord avec les CE 2 etCM 1 de l’école Aristide Briand) :

Ensuite une session spécial CM 2 (des écoles Aristide Briand et Jules Ferry) :

Et enfin une session à l’école Roland-Felix, concernant une classe de CM 1 et une classe de CM 2. Cette séance ne s’est pas faite avec le système suisse mais comme en 2024 avec une sélection par poule, pour savoir qui va en huitième de finale.

La préparation du tournoi a duré plusieurs semaines et s’est basée entre autres sur l’apprentissage de la notation algébrique, avec notation des coups au cours d’une partie :

puis reconstitution de la parte à partir des notes :

On voit au passage que le matériel de jeu a été assez facile à fabriquer (damier imprimé puis plastifié, graines peintes) :

Pour la suite il serait intéressant que les élèves construisent leur propre damier et que le tournoi ait lieu sur le damier préféré des élèves. Voici quelques exemples de damiers alternatifs (2 pions par joueur sur les damiers en Z, 4 pions par joueur sur les damiers en H) :