Ce cours a été donné en BTS analyses de biologie médicale. Il comprend beaucoup de chapitres au programme de maths (voire de spécialité maths-physique) en voie technologique.
Exponentielle et logarithme
Tout d’abord, en vue d’introduire le nombre e, on a besoin d’une notion liminaire, celle de variable :
Cette notion sera également utile lorsqu’on souhaitera évoquer, dans le cours sur les limites, les variables infinitésimales. Ensuite, on fait des révisions sur les suites géométriques :
Maintenant on introduit le nombre e, qui remplace 10 comme base d’exponentielle :
Après le nombre e, c’est à l’exponentielle de base e d’entrer en scène :
Sa réciproque, qui est le logarithme dit népérien, est vue après le cours sur l’analyse :
Analyse (calculs différentiel et intégral)
Le cours sur les limites est précédé par une initiation à la nomographie, avec ce nomogramme circulaire :
En effet il illustre graphiquement les propriétés multiplicatives des limites et notamment les formes indéterminées :
Les dérivées sont introduites par la notation de Leibniz :
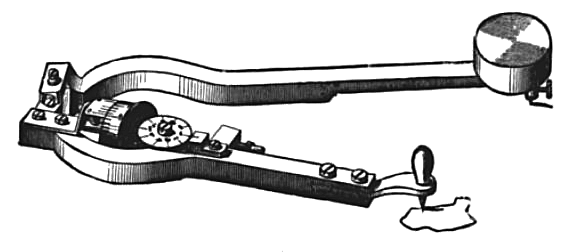
Les intégrales sont introduites à l’aide de planimètres (essentiellement de Prytz) :
Et les équations différentielles sont introduites avec la notation de Leibniz :
Probabilités et statistiques
Le cours sur la régression est basé sur les travaux du créateur de la notion, l’eugéniste Galton :
Les notations des probabilités se retrouvent dans les travaux de Bayes, créateur du concept de probabilité conditionnelle :
C’est également chez Bayes qu’on trouve des explications sur la loi binomiale :
La loi exponentielle est définie comme une intégrale :
Voici le nomogramme utilisé dans ce cours :
et celui sur la loi normale :
Enfin, le dernier chapitre de cours, sur la loi normale :
La fin du cours sur la loi normale porte sur ses applications à la statistique inférentielle.



Laisser un commentaire