Une camionneuse est chargée de faire des courses dans certaines villes, ou d’aller d’une ville à une autre, mais elle doit payer un certain nombre de jetons à chaque péage. Y arrivera-t-elle ? Comment payer le moins possible ?
Ce problème difficile a été soumis durant l’année scolaire 2023-2024 en IME et en Grande Section. En effet il permet de découvrir par la manipulation, le lien entre les nombres et leur écriture par chiffre, ainsi que les problèmes additifs, plus l’orientation dans l’espace. Le matériel de jeu est constitué
- d’un graphe pondéré (chaque péage est représenté par un chiffre indiquant combien de jetons il faut poser sur le péage),
- d’un petit camion sur lequel poser les jetons,
- de jetons (à placer dans la benne du camion) en quantité suffisante pour permettre à la camionneuse de réussir sa mission (d’ailleurs il lui est préalablement demandé d’estimer la quantité totale de jetons dont elle aura besoin),
- de papier et crayon pour noter l’ordre dans lequel ont été visitées les différentes villes.

Des questions comme de combien de jetons as-tu besoin pour faire le trajet ? ou te reste-t-il suffisamment de jetons pour traverser ce péage ? demandent une anticipation qui n’est pas toujours présente en Grande Section :
On a utilisé ces graphes, créés pour l’occasion :
mais il serait bon sans doute de leur préférer ceux-là, où il n’y a pas de chiffre (on pose un jeton à chaque péage) :
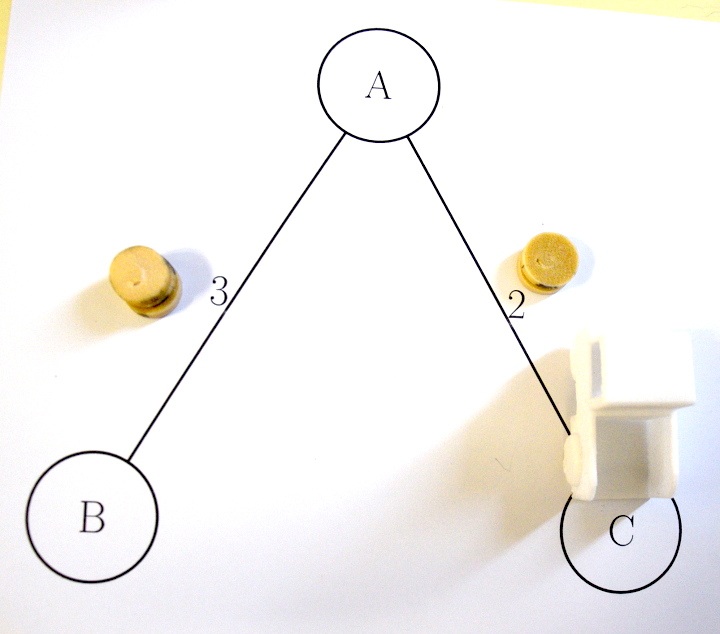
Ci-dessous, la camionneuse (partie de B) avait demandé 5 jetons (par essais et erreurs), puis payé 3 jetons au premier péage et 2 jetons au second péage. Il ne lui reste plus de jeton donc cela illustre le fait que 3 jetons + 2 jetons = 5 jetons :
On peut en faire une activité en grand, sur un circuit peint au sol (par exemple celui qui est utilisé pour l’initiation à la sécurité routière) avec des péages (guérites en carton, tenues par des élèves) et des trottinettes en lieu et place des camions. Une partie des élèves auront pour rôle de verbaliser ceux qui auront shunté un péage.
Une activité plus simple (parce qu’elle ne nécessite pas de passer par toutes les villes) est de trouver le chemin le moins coûteux entre deux villes données. Cela permet de voir comment la camionneuse cherche ce chemin : a priori elle mettra en œuvre un algorithme au programme de SNT.
Et si on cesse de distinguer les villes et les péages, on retrouve un célèbre problème d’Alcuin, paramétrable à l’envi. Par exemple cette version déjà intéressante :
On part de A avec 6 jetons, il y a une route allant de A à B (péage 1 jeton) et une route allant de B à C (péage 1 jeton). On ne peut pas mettre plus de 3 jetons dans le camion. Combien de jetons maximum peut-on amener en C ?
La solution a priori est celle-ci :
- En A, on charge 3 des 6 jetons (on ne peut pas faire mieux),
- on va en B (il ne reste alors que 2 jetons, à cause du péage),
- puis en C (il ne reste alors qu’un jeton),
- on dépose ce jeton en C
On a réussi à amener un jeton sur les 6 en C, et il reste 3 jetons en A.
On peut faire mieux (3 jetons en C) et pour savoir comment, rien de mieux que manipuler !



Laisser un commentaire